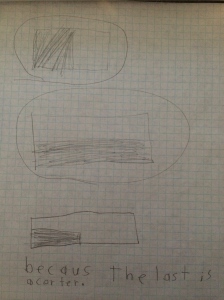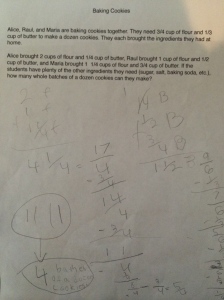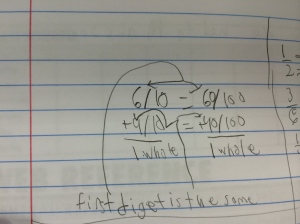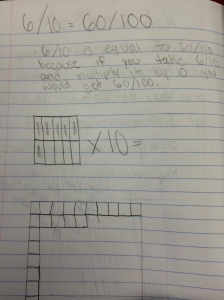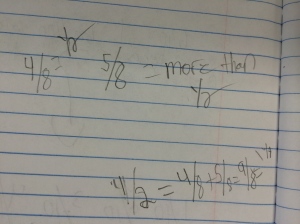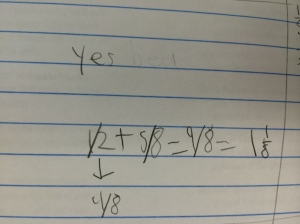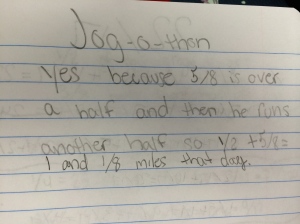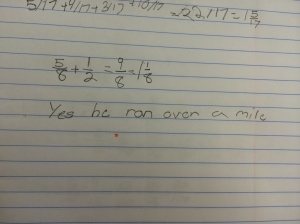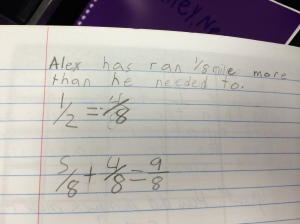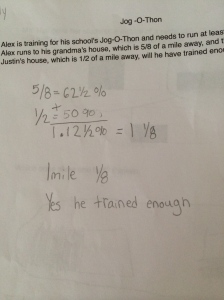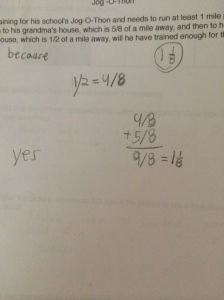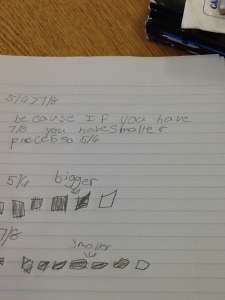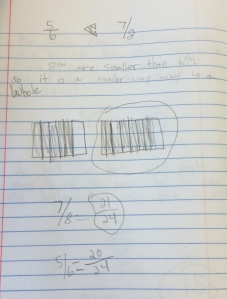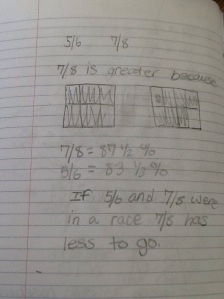Category Archives: Fractions

What Happens When You Divide by Zero?

This question got thrown out on Twitter the other day (full conversation here). It was something I had never thought about and struggled to think about where in our curriculum or standards it showed up. As always, I thought I would ask my students the following day what they thought happened when we divided by zero. Here are some responses:

It was interesting because most went to breaking into groups, but depending on how they reasoned about it,resulted in different answers. Sharing something between zero people or putting things into zero groups was either zero because there was nothing to put the number of things in OR it was that beginning number because they weren’t put anywhere and were leftover. Some also thought about inverse relationships which was nice and that is when our conversation got really confusing and people started questioning what in the world it was! One student punched it into his calculator and got Error, even more confusing while another asked Siri and got this, which they wrote in their journal…

Fawn tweeted a piece of student work that was really interesting in which the student had said 5 divided by zero was the same as 5/0, so (trying to quote this as accurately as I can) you cannot take five pieces of something with an area of zero. I am thinking that was like thinking something like 5/6 is 5 pieces when the unit is broken in to 6 pieces. In his case, it is five pieces with the unit cut into zero? Fawn, please correct me if I completely mess that one up!!

Very interesting and something I want to be sure I keep in the back of my mind. I love when a tweet can spark something I had never thought of before in elementary math work! Thanks Tina!

-Kristin

Volume with Fractional Dimensions

2 Replies

Before I began our volume work this year, I blogged about my planning process here: https://mathmindsblog.wordpress.com/2014/10/20/unit-planning/. As anticipated, I had many students who quickly developed (or already had) strategies for finding volume and could articulate a conceptual understanding of what was happening in the prism. In my previous post, I was throwing around the idea of giving those students dimensions with fractional length sides, so the other day I thought I would try it out. I did this Illustrative Task as a formative assessment of student understanding. Many students were done in a couple of minutes, with responses for part b that looked like this:

As I walked around the room and saw they were finished quickly, I asked them to revisit part b and think about a tank with fractional dimensions. Because of the great work they had done here I thought they would have some interesting thoughts. These are a few of the responses I got:

So, what did I learn from this work? I saw they had some great understandings about taking a fraction of one factor to make a number that they knew they needed to multiply by a third whole number factor to get 240. In the first two pictures, there is a great pattern happening that I want to explore further with the whole class. I also loved seeing that a student took the question “fractional length sides” to include decimals in his work. In my question, however, I had wanted them to consider more than one side in fractional lengths, however not being more explicit, they took it and ran with one side being fractional. In the next lesson, I thought I would push them a bit with this.

In the following lesson, students were finding the volume of an unmarked prism in cubic centimeters. They had rulers, cm cubes, and cm grid paper available to them, and went to work. Every year this happens, the Investigations grid paper works with the box to be whole number dimensions, however the cm are a bit “off” when using a ruler or cm cubes. I knew this, however, I do love the discussions that evolve from students who used different tools. I also thought this is the perfect opportunity for my students who were beginning to think about fractional sides. What transpired in the whole class lesson is a blog post in and of itself, however this is what came about from the fractional sides work…

Sooo much great stuff here! I had a group who was using the cubes, coming out with halves, but not wanting to round because it was “right in the middle” of the cube. I let them go and came back to see they were multiplying whole numbers, multiplying the fractions, and then adding them together to get their product. I asked them to think about another multiplication strategy to see if they got the same product, then came the array. Another student in the same group solved mentally to get the products. Unfortunately, the class had to leave me to go to their next class, also leaving me with so many things to think about. From here, I want to be sure students start to think about reasonableness of their solutions, compare their fraction multiplication strategy to whole number multiplication strategies, and think about how we multiply three numbers (Associative property). So much to do, I need full day math classes!

-Kristin

“Is this really just multiplication?”

7 Replies

After a couple of weeks working with problems in which they were taking a fraction of a fraction, fraction of a mixed number, the students made some conjectures about the problems.

We went through each one, proved, disproved and refined them when finally one student just asked..

“Ok, isn’t this really just multiplication?”

I knew he just wanted an answer, but that was not going to happen. 🙂 Since we have been doing a lot of multiplication number talks, I thought I would see if I could make a connection to whole number operations.I said, “Well, if it is multiplication, do you think the strategies on our anchor chart should work for the fractions too?” We made the anchor chart as strategies arose in our number talks. I put 2 1/4 x 1/2 on the board and said, “Try it out.”

They worked in groups and came up with some pretty amazing stuff…(A couple students chose to try a different problem, so the sampling below may be a mix)

We are going to share some strategies tomorrow since the rest of the class period consisted of them “arguing” about fraction multiplication. It made my day when one of the girls was leaving my class and said to her friend, “That was so fun!”

Wait, fractions fun?? LOVE IT!

-Kristin

Student Work with Fractions

1 Reply

I do not have much time to write this morning, however I know how much I love looking at student work, so I thought I would give some of my friends who love doing the same some stuff to look at this morning!

For a future PD I am doing on fraction progression, I wanted some thinking around this Illustrative Math problem: https://tasks.illustrativemathematics.org/content-standards/3/NF/A/1/tasks/833 This is a 3rd grade CCSS, so I had some beginning of the year 4th graders this task to try out. Here are some samples:

And this Illustrative task: https://tasks.illustrativemathematics.org/content-standards/2/G/A/3/tasks/827 It is a 2nd grade CCSS so I gave it to beginning of the year third graders this year.

This task (https://tasks.illustrativemathematics.org/content-standards/6/NS/A/1/tasks/50)is a 6th grade CCSS, these are my students from last year who are now in 6th grade:

This task is 4th grade CCSS: https://tasks.illustrativemathematics.org/content-standards/4/NF/C/5/tasks/154, this is my current 5th graders:

Same group of students on this task: https://tasks.illustrativemathematics.org/content-standards/5/NF/A/1/tasks/855

And then finally, in my class we were comparing fractions. I asked them which was greater 7/8 or 5/6 and how they knew…

Have fun math peeps! I would love to chat in the comments or on Twitter about any/all of them!

-Kristin

Fraction-to-Decimal Division Table Noticings

7 Replies

Last week, I did an investigation on identifying fraction/decimal equivalents and interpreting fractions as division. In previous years, I have to admit, I never fully appreciated this lesson. I could never get a grasp on how to not lose all of the great understandings students have about fractions and make it about division with the calculator. However after last week’s work, I have a new appreciation for the conversations it brought out in the classroom.

Throughout the year, we have worked with decimals, fractions and percents, so I feel my students are very comfortable moving between the three notations. They see the relationships between the decimal and percents for the /2s , /3s , /4s, /5s, /6s , /8s, and /10s and know the percents for many (if not all) of those fractions because of our work on the 10×10 grid.

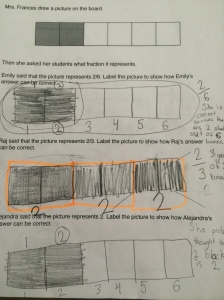
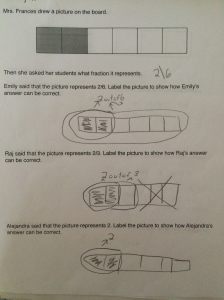
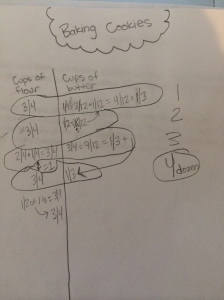
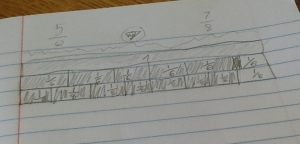
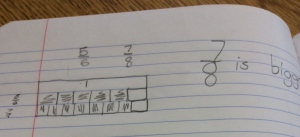
I opened this lesson with a fraction I was sure they knew the decimal for, 1/2. I asked them how they think we could use a calculator to find the decimal if we did not know it. They played around for a while and as I walked around many students could tell me they divided the numerator by the denominator. I asked if that same method worked for 1/4? As a class, they agreed it worked every time, so I asked why they thought that was so. Why are we getting a decimal? Many said with 1/2 we had “one whole divided into 2 pieces, so each piece has to be .5 so they both add to 1 whole.” Another said we only get a whole number when “it is more on top then the bottom.” I felt comfortable after a lot of talking from the class that they were seeing the fraction bar as division. So, we moved along to the division table. I had a student explain how a multiplication table works and then explained the numerator and denominator row and column in this decimal table. We looked at 1/2 and filled in the 0.5. I asked where else that decimal would show up in the table and they filled in the equivalents of 2/4, 4/8…etc. From there they worked with their partner to complete the table.

I teach two classes of math (thank goodness) so I can change up things that didn’t work as expected the first time. In the first class, I let them use their calculator from the start of the table. I realized as I walked around that students were completely losing their sense of fractions and it became a calculator exercise…exactly what I was afraid was going to happen. I saw students filling in by column and using the calculator in the tenths row! Big Fail on my part. I stopped all calculators, told them they had 5 minutes to work without the calculator to complete all of the decimals they could. The conversation took a dramatic turn for the better! They started to see that working in rows helped them see patterns and used their knowledge of equivalents to complete other cells and honestly moved along much faster! Needless to say, I started the next class without the calculator and the students liked the challenge of trying to reason about the empty cells without the calculator. Here is a sample of one of my student’s completed table:

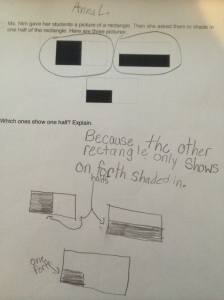
For homework, I asked the students to write at least five patterns they saw in the table, either as they were completing it or after reflecting back on it. Here are some journal entries: As a class, we came back together the next day and collected our noticings on the board:

Period 1:

Period 2:

We had some that we agreed on, some we disagreed with and others we had to reword to make it agreeable for everyone. I found in that class period the meaning of this lesson for me…it wasn’t so much about completing the table by using division, which was my previous aversion to this lesson, but instead about finding patterns and digging into why those patterns were happening.

I would love to go through each one and tell you about our discussions, however to be honest, I have so many other things I have to get done before class tomorrow! I hope to follow up with a future post on our decimal discussions.

However I do have one thought/question I am still grappling with that I would love some thoughts on..

One student noticed that the elevenths “goes up by multiples of 9 in the tenths and hundredths.” They clarified by writing the decimals (rounded to the thousandths) on the board for us: 0.091, 0.182, 0.273, 0.364, 0.455…etc. The class could see where the multiples of 9 were showing up. Then one student noticed that the tenths was going up by one, the hundredths was going down by one, and the thousandths up by one.

At that moment, this sounded like the multiples of 9, the ones place decreasing by one and the tens place increasing by one. Now with the whole numbers you are adding a ten and taking one away to add the 9, so I see that…and for the elevenths, you are getting one more piece then tenths, so are you adding a tenth and then taking a hundredth away? Is that for the same type of reasoning? Then the thousandths? I will be busy procrastinating other work to play around with this tonight 🙂 Any thoughts welcome!

-Kristin

You Never Know What They Know Until You Push Their Thinking….

Leave a reply

Last Friday, at a state math meeting, we had so much fun diving deep into a fraction lesson of a 6th grade teacher. The lesson was on multiplying fractions by fractions and while the conversation started with thoughts about the lesson itself and areas for discussion for the math coach, the lesson really brought to light the fraction progression. I cannot even begin to recap all of the insightful discussion points such as using models and the importance of the representation in mathematics, teacher pedagogy and mathematical understanding, vertical articulation across grade levels….I could go on and on, but I had one brief conversation that leaked its way into my classroom the following Monday.

While we were “doing the math” the students would be doing in the lesson video, a colleague and I were talking about where our 5th graders leave off with fractions and how that is built upon in 6th grade. She made the comment that if the students truly understood taking a fraction of another fraction and fraction of a whole number (both 5th grade standards), then they could reason their way through mixed number times mixed number, which is introduced in 6th grade. She quickly drew out 3 1/3 x 3 1/3 and we talked through the context in which our book uses and how students could reason about that problem.

So, of course, I have to throw it out to my students on Monday because I am curious at this point if they could work their way through the problem and the various ways they would think about it. This is where that “engaging” vs “not engaging” or “real world” vs “not real world” conversation seems void. I used no context, no real world example, I simply said, “I was talking to some middle and high school teachers at my meeting on Friday about your fraction work and they were wondering how you guys would solve this problem. 3 1/3 x 3 1/3.” They went to work and I started walking around to chat with them.

Here are some strategies I saw…

She started with 3 1/3 x 3 and then added another 3 1/3 and found 1/3 of that to be 1 1/9.

He used partial products. When I asked him how he figured that out, he wrote the 25 x 25 and explained how he gets his partial products there so he did the same thing with wholes an fractions. Wow. Did not expect this one!

Same partial products, just a bit neater!

She used separate bars for each 3 1/3 and then divided the bottom up to find the 1/3 of 3 1/3.

I was so impressed by the work of these kiddos and they were so proud of themselves! They connected understandings of whole number operations to fractions, applied properties of mathematics, used what they knew conceptually about fractions to model the situation, and most importantly persevered through the problem and constructed arguments about their answer.

Don’t get me wrong, it wasn’t all picture perfect….I did have some who initially gave me 9 1/9 (as I anticipated they multiplied the whole numbers then the fractions and put them together) but that led to a great “reasonableness” conversation. A context in this case helped some students see that if you did 3 laps that were 3 1/3 miles long it was 10 miles, so if you did a 1/3 longer, can your answer be less than 10?

Needless to say, I don’t know how anyone doesn’t just love hearing students talk about math and reason about problems. I find it energizes me, my students, and the climate in my classroom. So, thank you to MSERC (University of Delaware Math & Science Education Center) and the Delaware Math Coalition for all of the hard work that is put into making these professional development opportunities so rewarding for both myself and my students! I think you all are AMAZING!

-Kristin

Math & Minecraft Day 1

3 Replies

After many days of discovering my HUGE learning curve with Minecraft, I am finally starting to feel relatively comfortable in Creative mode…I can build a house without flooding it, planted a few trees and I no longer have random blocks floating in the sky around my world! My class has been staying with me during recess to teach me how to play and I am amazed at how fast and detail-oriented they are in their designs, such as putting lava rocks under the water blocks to form a hot tub and putting glass windows in their new greenhouses. I just kept thinking that I would love for them to use this same precision and perseverance in math class.

I must have Minecraft on the brain, because I as I was planning this weekend for the upcoming week (multiplying fractions w/arrays), all of the scenarios were about planting on an acre of land. For those who may not know, Minecraft is based in cubes that can be planted in the ground to show a square, perfect for our gardens. I came up with this scenario…

I honestly lost sleep last night anticipating student responses because I knew some students would look at it as fraction of a group of blocks in this scenario, when I wanted it to be fraction of a one whole. Ideally (whatever that really is) I students would build the garden, split the fourths and divide 3 of the fourths in half to result in 3/8 of the garden (being the whole) being melons. But as they got into groups today, hopped into each others worlds and went to work it was quite a variety of outcomes.

As I expected, many students did it as fraction of a group of however many squares were in their garden. Here is an example of this: http://www.educreations.com/lesson/view/sammy/14346123/?s=sXGl7c&ref=link

This one was interesting because they did a combination of staying with the garden as a whole and then in the end went to the number of blocks were planted with melons: http://www.educreations.com/lesson/view/steve-s-garden/14349675/?ref=link

This one was great because they brought back the fraction bar model we had been previously working with and had it next to their Minecraft garden. (Plus you have to Love their answer): http://www.educreations.com/lesson/view/garden/14361270/?s=tk0bLr&ref=link

Ignore my loud voice in the background on this one, but it is a very great build (and with a key): http://www.educreations.com/lesson/view/dylan/14361243/?s=Qt3Ws8&ref=link

When they completed their garden, I gave them a square and told them that it was one acre and I wanted them to represent the same scenario but on the open square. I immediately saw confusion in the students who had saw the garden as 16 blocks vs the students who saw it as one whole garden.

Here are a few example answers:

http://www.educreations.com/lesson/view/kurtis/14360404/?s=xWw8UW&ref=link

http://www.educreations.com/lesson/view/riley/14361043/?s=FbOohc&ref=link

This one has some interesting talking points (a little long). You can forward to minute 3:00 for the blank array: http://www.educreations.com/lesson/view/steve-s-garden-kyzei-and-aiyana/14360241/?s=hRV0CF&ref=link

*We also had some great conversations about deciding about the dimensions of the garden and the denominator being a factor of the dimension since we couldn’t split the blocks. For example, many students built a 5 x 5 and went to break it into fourths. They said, “four is not a factor of five so we can’t.”

Lots of sharing to do tomorrow and discussing strategies, notation and the whole in the problem….stayed tuned for Minecraft Day 2…

-Kristin

Number Talks – Fractions

12 Replies

Through doing Number Talks with students K-5, I started to realize that one thing I look for students to use in our whole number computation discussions is using known or derived facts to come to a solution. I feel like the problems I have been using are crafted to use the answers from previous problems to reason about the ending problem.

In the younger grades, I would like to see students using the double known fact of 7+7=14 to know 7+8=15. I want them using 23 + 20=43 to get 23 +19 = 42. I don’t want them treating every problem as if they have to “start from scratch” adding all or adding on.

An example in the upper elementary:

18 x 2

18 x 20

18 x 19

This progression leads them to use a known or derived fact (18 x 20) in order to solve 18 x 19. To build efficiency, I don’t want them to the treat the final problem in the progression as a “brand new” problem in order to reason about an answer.

Along these lines of thinking, as I observed students working the other day, I realized that students weren’t using this same use of known/derived facts when working with fractions. For example, a student was adding 3/4 + 7/8. He used 6/8 as an equivalent of 3/4, added that to 7/8 and ended with an answer of 13/8. Don’t get me wrong, I loves his use of equivalency and I am a fan of improper fractions, however I started wondering to myself if it would have been more efficient (or show that he actually thought about the fractions themselves) if he used a fact he may have known such as 3/4 + 3/4=1 1/2 to then add an 1/8 on to get 1 5/8? Or used 3/4 + 1 = 1 3/4 and then took away an 1/8? Is that the flexibility I want them using with fractions like I do with whole numbers?

I thought I would try a Number Talk the following day to see….

1/2 + 1/2

Thumbs went up and they laughed with a lot of “this is too easy”s going around.

1/2 + 1/4

Majority reasoned that 1/2 was the same as 2/4 and added that to 1/4 to get 3/4. Some said they “just knew it because they could picture it in their head” I asked if anyone used what they knew about the first problem to help them with the second problem? Hands went right up and I got an answer that I wish I was recording. It was to the effect of,”I know a 1/4 is half of 1/2 so the answer would be a 1/4 less than 1.”

1/2 + 3/4

Thumbs went up and I got a variety here. Some used 2/4 + 3/4 to get 5/4 while others decomposed the 3/4 to 1/2 + 1/4, added 1/2 + 1/2=1 and added the 1/4 to get 1 1/4.

3/4 + 3/4

Got some grumbles on this one, because it was “too easy” – 6/4…Duh! The class shook their hands in agreement and they were ready to move on to something harder. I noticed that when the denominators are same, they don’t really “think” about the fractions too much. I waited….finally a student said, “It is just a 1/4 more than the previous problem so it is 1 1/2″ and another said each 3/4 is 1/4 more than a 1/2 so if you know 1/2 + 1/2 = 1 then you add 1/2 because 1/4 + 1/4 = 1/2.” I had to record that reasoning for the class bc it was hard for many to visualize.

3/4 + 5/8

Huge variety on this one and I thoroughly enjoyed it! From 6/8 + 5/8 = 11/8 to decomposing to combine 3/4 and 2/8 to get the whole and then 3 more 1/8s = 1 3/8. There were many more students who used problems we had previously done.

What I learned (and questions I still have) from this little experiment:

– Students LOVE having the same denominator when combining fractions.

– Do they really “think” about the fractions when the denominators are the same? Can they reason if that answer makes sense if they are just finding equivalents and adding.

– Students can be flexible with fractions if you push them to be.

– Subtraction will be an interesting one to try out next.

– I would much prefer if I remembered to use the word “sum” instead of “answer”…. I tell myself all of the time, but in the moment I always forget.

– Using known or derived fact and compensation are invaluable for students when working with both whole numbers, fractions and decimals.

– Are there mathematical concepts that present themselves later in Middle School or High School in which known and derived facts would be useful?

Happy Thanksgiving,

Kristin

Modeling Mathematics – Developing the Need

Leave a reply

Today we were talking about things we noticed as we worked with finding a fraction of 1/2. Students are noticing things I expected: that the denominator doubles each time, the numerator is staying the same as the fraction you are dividing the half up into, some are starting to notice that the numerators are multiplying and so are the denominators, and some are just flat out complaining that they have to model it on the fraction the bar.

So the fraction of 1/2 was pulling some great noticings, however I wanted the students to feel the value of being able to model the mathematics, to show what was happening, so I asked them what would it look like if I had 3/4 of a candy bar and wanted to split it with two friends. What fraction of the whole bar would I get?

I was excited that some labeled the 3/4 on a fraction bar with 6/8 and then split that in half and labeled 3/8. They said they “knew half of 6/8 was 3/8” I asked why didn’t they work with 3/4, they explained that splitting the three was not working and 6 was easier because it was even.

Some said they had split the 3/4 in half and it looked about like a 1/3, so it was 1/3. I appreciated the estimations, but looking for them to dig further after they estimated.

I would say that a third of the class had written 3/4 of 1/2= 3/8 with a fraction bar 3/4 shaded and then split in half and labeled 3/8. When asked how the fraction bar modeled their answer, they told me that they didn’t “need” the fraction bar to find the answer, they noticed that you multiply the numerators and denominators. “Can’t we just give you the answer?” “It’s the right answer, right?”

We don’t “need” the fraction bar. Huh.

Then an interesting thought hit me….they see pictures as a tool they don’t need rather than a model of a mathematical situation. It almost seemed as if they viewed the bar as “baby-ish” to use. You know how certain things hit you as WoW?!? That is completely what that comment did. I immediately started to reflect on how I had made the fraction bar sound…did I just make it sound like a way to solve? Did I even use the word model? Am I placing too much emphasis on the modeling piece?

I can see why students view diagrams as a way to solve….when they learn to add, they draw pictures. When they first work with “groups of” they draw pictures. When they first work with arrays, they draw things in row and columns. Once they have learned how to add, the pictures aren’t necessary. When they have learned how to multiply, the arrays and groups of aren’t seen as a necessity.

In that moment, I wanted the students to appreciate how important (and difficult) modeling is in mathematics. I pushed them to explain how to name that line drawn at half of the 3/4 and we had some great conversations about why this was more difficult than a fraction of 1/2.

In the end, I assured them that I sit with adults all of the time and we struggle (and find MUCH enjoyment) in making models of mathematical situations. They felt ok with knowing it wasn’t just tough for them and I felt ok that they could see a “need” for their fraction bars!

-Kristin

Fraction of Fraction Day 2

Leave a reply

As I mentioned in my previous post: https://mathmindsblog.wordpress.com/2013/11/15/fractions-of-fractions/
I had wondered about fraction multiplication being introduced without a context when the students were coming from lessons in which a fraction of a whole/mixed number had a context. Feeling like the students had a solid grasp on how to find a fraction of a fraction on a fraction bar, I thought I would try having them develop a story context for fraction multiplication problem. They had free reign of the fractions they used and context they chose. Needless to say, it was a learning experience for me. Some showed understanding of what they were doing when finding a fraction of a fraction of something while others unveiled some things I need to go back and revisit.

I have included clips from some of their videos and what I learned from each…. (turn your volume up bc they whispered on these)

http://www.educreations.com/lesson/view/aiyana-fraction-bars/13628710/?s=fv1sHe&ref=link

This one was SO interesting (and a little humorous) because she cut the fraction bar to find 2/3s of 1/2, however when she is explaining her reasoning she used the commutative property. Saying that the answer is 2/6 because that is half of 2/3 was something I had never thought of exploring with students when reasoning about whether the answer made sense. I loved it and definitely added to my lessons for next week!

http://www.educreations.com/lesson/view/riley-s-breadstick-word-problem/13630693/?s=j3i9i5&ref=link

When she introduces the scenario, she says “1/2 of 1/4” so I don’t know if she misspoke or not really understanding the context. I can see she has the process but I don’t know if the understanding is there. I do love how she says “He wanted to find how much of the whole bread stick that was” because she is relating her answer back to the whole. This was difficult for many students. Maybe picky on my end, but I would have liked for her to label the pieces 1/8, 2/8, etc instead of by whole number, even though I know she is counting the pieces.

http://www.educreations.com/lesson/view/ab-word-problem/13627803/?s=Hr3zRv&ref=link

I was impressed how she used a class of students as the whole and did not get confused with the fraction of the class as opposed to the number of students. Many others got caught up in “How many students…” instead of “What fraction of the class.” One thing that just bothered me in watching it was the empty seat in the class! I just wanted to draw a person in for her!

http://www.educreations.com/lesson/view/kyra-s-problem/13628055/?s=aIYKAt&ref=link

This one has such a great context and division of the Hershey Bar that I was so excited, until the end. She seemed good with the context, decontextualized to solve, but then struggled to recontextualize to explain the answer.

I could post and comment all day, but needless to say there is other work to be done and papers to be commented on! It was a great first day with our 1:1 iPads using Educreations! I learned so much that now I must work on readjusting my math plans for next week!

-Kristin

MathMinds

by Kristin Gray.

Category Archives: Fractions

What Happens When You Divide by Zero?

Volume with Fractional Dimensions

“Is this really just multiplication?”

Student Work with Fractions

Fraction-to-Decimal Division Table Noticings

You Never Know What They Know Until You Push Their Thinking….

Math & Minecraft Day 1

Number Talks – Fractions

Modeling Mathematics – Developing the Need

Fraction of Fraction Day 2