Category Archives: Uncategorized

Low Floor, High Ceiling, Wide Walls: Using Tasks to Elicit and Leverage Ideas

The answer is 1/2. What is the question?

Pause for a moment to think about how you would respond to this prompt. After you have a question in mind, reflect on the thinking you did to come up with that question. What topics did you think about? Did they include mathematical representations, a real-world context, or calculations? Something else?

Last week, we had our second book study session for NCTM’s Teaching Mathematics Through Problem Solving K–8. The focus of the session were chapters four and five around instructional tasks and teaching signposts that support students in learning through problem solving. We wanted to open the session with a good math prompt as everyone was arriving, a prompt that gave them something interesting to think about as we waited a couple of minutes and also set the tone for the learning we were going to do together. Since the session was focused on instructional tasks, we wanted to begin with one that reflected what we value in classrooms—tasks that invite everyone in and elicit a wide array of student thinking.

After a few seconds, the chat was buzzing. Here is a sampling of the amazing responses we got.

The variance in responses was so fun and got me thinking about when, where, and with whom a prompt like this might be especially powerful. I often use tasks like this to launch a unit, lesson, or activity so I can learn how students are thinking about the mathematical concept we are about to explore.

Launching a Lesson

A former colleague, Jenn, used this prompt to launch a 3rd‑grade lesson on comparing fractions. Using the task at this point in a lesson not only provided insight into students’ thinking, but also supported differentiation. Students who finished early had access to a bank of questions to evaluate, compare, and justify. Even better, those questions came directly from the students themselves.

Launching and Wrapping Up a Unit

Building on this idea, what might it look like to use a prompt like this not just to launch a lesson, but to bookend an entire curriculum unit?

Before beginning a unit on fraction multiplication and division in 5th grade, we might pose the question, “The answer is 3/4. What is the question?” At the start of the unit, we would likely see fractional diagrams, addition expressions such as 1/4+1/4+1/4, or multiplication expressions like 3 ×1/4. All of these responses are incredibly valuable for eliciting what students currently understand about fractions.

By the end of the unit, however, students have developed new understandings about fraction multiplication and division. Revisiting the same prompt invites them to apply those new understandings in more sophisticated ways. Building on the original list of student‑generated questions at the end of the unit could serve as a powerful formative assessment and, just as importantly, a rich anchor chart that documents students’ learning over time.

Professional Learning

This idea also extends naturally to professional learning settings, particularly those that bring together educators across a wide range of grade levels. For example, in professional learning focused on the fraction learning progression, the list we generated at the beginning of our book study session would be invaluable.

A rough draft PD flow could look something like this:

Pose the prompt and ask teachers to write their responses on index cards.
In small groups, teachers share their questions and work together to align them to grade‑level standards.
In larger groups, teachers collaborate to form a learning sequence, ordering the cards from the earliest fraction understandings to the latest.
Teachers move into grade‑level groups to identify their curriculum unit in which they could use a prompt like this. For K–2 teachers, this would mean adjusting the prompt to use the words “one‑half” instead of a numerical representation (a variation I used in 1st grade).
In grade‑level groups, teachers anticipate what students might say and plan how they will leverage student understanding and use student‑generated questions.
The whole group shares ideas.

Reflection

Coming back to the book study, I found this book quote reflective of prompts like these:

Activities that provide access and extension are often referred to as having a low-floor and high-ceiling. Meaning, the problems invite all students to engage, while also providing space for deeper exploration. These types of tasks provide accessible entry points without lowering or limiting the cognitive demand of the mathematics. Mitch Resnick (2020) takes this idea even further with the concept of “wide walls,” which reminds us that learning shouldn’t just move from easy to hard, but should also give students space to explore ideas in different ways and directions.

Coming Up

If this prompt has you thinking about your own classroom or professional learning spaces, I’d love for you to continue the conversation with us. Join me on February 9 for a free webinar with Ashley Powell and Shawn Wigg as we explore instructional tasks that invite a wide range of thinking. We will relate the ideas in the NCTM book to practical applications of tasks in the classroom. Participants will receive an excerpt from the NCTM book, and we’ll raffle off a free digital copy at the end. Hope to see you there!

Mathematizing Children’s Lit & Some of My Favorite Books: 2nd-5th Grade

Leave a reply

In my previous post, I ran through some lessons I’ve learned about interactive read alouds and shared a few of my favorite books for K–1. And while many of those books can absolutely stretch up into grades 2–5, there are others that, because of their math content or overall reading complexity, are a better fit for this upper‑elementary grade band. So today, I’m sharing a set of book recommendations that support joyful exploration and productive mathematical discussions! These titles open space for noticing patterns, justifying ideas, engaging in debate, and connecting mathematical thinking to the world around them.

And if you’re working across multiple grade levels, you can always revisit my earlier K–1 read‑aloud list. Together, the two posts offer a collection of my favorite books that invite curiosity, support authentic access to the mathematics, and build a shared mathematical community from kindergarten all the way through fifth grade.

Concept	Book Suggestions
Number and Operations	Equal Shmequal by Virginia Kroll One Is a Snail, Ten Is a Crab by April Pulley Sayre and Jeff Sayre One Hundred Hungry Ants by Elinor J. Pinczes A Remainder of One by Elinor J. Pinczes How Much Is a Million? by David M. Schwartz 100 Mighty Dragons All Named Broccoli by Larochelle & Cho Dozens of Doughnuts by Carrie Finison Hello Numbers by Harriss and Hughes
Fractions	The Lion’s Share by Matthew McElligott Fry Bread by Kevin Noble Maillard Give Me Half! by Stuart J. Murphy The Doorbell Rang by Pat Hutchins How Many Ways Can You Cut a Pie? by Jane Belk Moncure
Measurement and Data	Spaghetti and Meatballs For All! by Marilyn Burns How Big Is a Foot? by Rolf Myller The Penny Pot by Stuart Murphy Curious Comparisons by Jorge Doneiger Coa Chong Weighs and Elephant by Songju Ma Daemicke Greater Estimations by Bruce Goldstone Actual Size by Steve Jenkins Which Would You Rather Be? by William Steig
Geometry	This is Not a Maths Book by Anna Weltman (not really a children’s book, but it is sooo good!) Which One Doesn’t Belong? by Christopher Danielson Shapes, Shapes, Shapes by Tana Hoban Grandfather Tang’s Story by Ann Tompert

I hope this collection gives you fresh inspiration for sparking mathematical curiosity in your classrooms. The best way to know whether a read aloud resonates with yourself and students is simply to try it. You can see how your students respond, notice the ideas they generate, and decide how to leverage their thinking toward the learning goal.

Give these titles a spin, and let me know what mathematical conversations they open up for you and your students. I’d love to hear what you try!

IG: @kgraymath and LinkedIn

Adapting Lessons Part 3: Engaging with Word Problem Contexts

Leave a reply

Word problems have always been challenging for me as a teacher and as a coach supporting teachers. I think part of the reason is that you can’t really teach word problems in the traditional sense. Solving them depends on students making sense of a situation and the question they are being asked to answer, and there are many factors that influence that sensemaking.

One factor is the context itself. I know how important it is for students to apply their understanding in both familiar and novel situations; however, every context will be a mirror for some students and a window for others, and when a situation is completely unfamiliar, I have seen it significantly impact how students approach the problem. Another major factor is the language of the problem itself. Many word problems include vocabulary, sentence structures, verb tenses, and multiple steps that shape how students make sense of the situation. These features require them to draw on things like reading comprehension, syntax, semantics, and sequential thinking, not just mathematical understanding and procedural skill. All of these elements influence the mental model students build based on the context and ultimately affect how they attempt to solve the problem.

Because of these complexities, it is not surprising that many students quickly grab numbers from a word problem and compute or search for key words. These strategies often worked for them in earlier grades, with one-step problems, or within curriculum units focused on particular operations. As a result, they do not always read the context as something that should make sense. Instead, they read while thinking, “Which operation do I need to use to solve this problem?” This reminds me of times when I am reading a book with something else on my mind. Even though I am technically reading the words, I can finish an entire page, or even a chapter, and realize I cannot remember anything I just read. I think this is similar to what happens when students read a word problem while also trying to figure out how they are supposed to solve it.

Understanding these challenges gives us important insight into the kinds of instructional adaptations that best support students in sensemaking. When we pause and give students an opportunity to make sense of a context before jumping in to solve, we set them up for more productive problem solving. And, the more we provide these opportunities, the more metacognitive those ‘sense-making structures’ become for students. There are some great math language routines out there, such as Three Reads and Co-Craft Questions, that are productive in a whole-group setting, but can take a lot of class time, require preparation, and may not transfer easily to a new problem for students. Because we sometimes can’t predict the problems that will be most challenging, I also like to have a few back-pocket, in-the-moment adaptations that promote the same type of reasoning and sensemaking.

These adaptations are all about helping students make sense of a word problem before they jump into solving. By giving them time to notice, wonder, visualize, and pose questions, we make the problem more accessible and give students the chance to build a strong mental model. This approach draws on both math and language skills, helping students focus on understanding rather than just grabbing numbers or looking for key words. When we use these adaptations in the classroom, students are more likely to engage in deeper, more productive mathematical thinking and problem solving.

For more ideas and examples, you can check out some related blog posts:

Brian’s Numberless Word Problems: https://numberlesswp.com/
My blogs on Numberless Word Problems: https://kgmathminds.com/category/numberless-story-problems/
My blogs on Problem Posing: https://kgmathminds.com/category/problem-posing/

And of course, if you missed the first two posts in this series, you can find them here:

I look forward to hearing about what you might try! You can share here in the comments or over on IG: https://www.instagram.com/kgraymath/

Adapting Lessons Part 1: Launching an Activity

2 Replies

As a math teacher and coach, I’ve always adapted curriculum materials. I am sure we all have—it’s part of knowing our students and wanting to provide them with access to the math in ways that make sense to them. And while we have the best of intentions, sometimes the choices we make can unintentionally take the math out of students’ hands, disconnect from what they already know, or even reflect assumptions and expectations we didn’t realize we were holding.

Adapting activities is challenging for many reasons: some decisions require extensive prep, others happen in the moment, and all of them must be balanced with the pressure to keep pace while still giving students the time and space to share the incredible ideas, experiences, and mathematical thinking they bring into the classroom. I also found it difficult at times to know exactly what to look or listen for mathematically, and I sometimes interpreted students’ responses through my own assumptions and expectations. While a high-quality curriculum can provide problems that elicit student thinking, the deeper work of examining what we notice, what we value, and how we interpret and leverage students’ ideas extends far beyond even the most comprehensive teacher guide.

While thoughtful planning ahead of time is ideal, we all know it isn’t always possible. Because so much can get in the way of planning and prep time, I think a lot about how to make quick, in-the-moment adaptations based on what students are saying and doing—and on what I still need to learn about their thinking. I often wonder: What if our adaptations did more than simply “fix” a lesson? What if they opened space for deeper student thinking, a stronger sense of community, and richer mathematical understanding?

These questions keep pushing me to look closely at the flow of a typical lesson and identify the moments where even small adaptations can make a big difference. I’ve found that there are five points in a lesson where a few quick, minor changes can have a big impact:

Launching an activity
Working in small groups
Engaging with contexts
Sharing ideas
Synthesizing the lesson.

While it would be wonderful to have a single “right” adaptation for each of these, the reality is that different classrooms and moments call for different routines or structures. In the next series of posts, we’ll take a closer look at each of these opportunities and explore practical, in-the-moment ways to adapt them.

Ultimately, the goal of these small adaptations isn’t just to adjust an activity or lesson; they’re meant to open up richer mathematical experiences for students and provide increased insight for teachers. My hope is that these structures encourage sense-making and increase access to the mathematics; provide every student opportunities to share the amazing ideas they bring; create space for questions about one’s own or others’ thinking; build a stronger mathematical community; and support teachers in reflecting on why they’re adapting an activity and how those choices best serve students.

In this post, I’ll outline a few alternate ways to launch a lesson, and in subsequent posts, I’ll explore each of the other lesson moments listed above.

Alternate Ways to Launch a Lesson

Instructional Goal: Provide students with an entry point into the activity.

When deciding which adaptation to use, it is helpful to think about what aspect(s) of the task might make it inaccessible to your students. For example:

If the context or representation of the problem might be unfamiliar to students, you could use the Tell a Story, What Questions, or Making Connections routine.
If the activity relies on a prior knowledge from earlier in the year or prior grade levels, it might make sense to use the What Questions or Making Connections routine.
If the language (including math language) adds a layer of complexity to the activity, you could use the Word Splash routine.

Try it!

There isn’t one “right” adaptation for any classroom scenario; each is an opportunity to learn more about your students. In the end, it’s not the routine itself that matters as much as what the routine affords—the ways it reveals student thinking, provides an entry point, and supports problem solving. The only way to figure out what works best is to try these structures out! Fortunately, they require little materials prep. All you need is a piece of chart paper or whiteboard and an image from the problem students will be solving.

In your next PLC or planning session, review the activities in an upcoming lesson. As you read through each problem, discuss:

What knowledge and experiences are your students bringing to the problem?
Is there an activity where students might not have access to the problem? If so, what specifically is inaccessible and why?
Which of the four routines will you use to launch the activity?*

*If you’re planning with your grade-level team, each person can try a different routine and then compare the affordances of each one. I’d love to see what you try! Share your ideas in the comments or on IG (@kgraymath)!

Part 2: Supporting student learning as they work in small groups

Two Math Routines to Learn About Student Thinking

1 Reply

Routine 1: Tell Me Everything You Know About ____________

Directions

Choose a word or phrase that is the focus of your first curriculum unit. This could be something like: fractions, addition and subtraction, shapes, data, multiplication, etc. If students are introduced to that concept for the first time during the unit, such as volume in fifth grade, use a term like ‘measurement’ to elicit prior knowledge related to volume.
Write your chosen concept or topic at the top of a piece of chart paper.
Prompt students, “Tell me everything you know about [your chosen topic].”
Give students 1 minute of independent think time and then 1 minute to quickly tell a partner one thing they are going to share with the whole class.
As a whole group, record students’ ideas on the poster as they share.
When they are finished, ask if there are any ideas on the chart paper they have questions about. This is a good opportunity for students to ask clarifying questions of one another, revise their thinking, and agree or disagree with others’ ideas. You do not need to come to a final conclusion on each point of disagreement, especially if it is something they will learn in the unit. Simply just mark that idea with a question mark and revisit it later.
If there is time, you could start another poster with the prompt, “Tell me everything you wonder or have questions about [your chosen topic].” This communicates that sharing things they wonder and asking questions are part of learning. The information you’ll learn about student thinking will be extremely helpful going into the first unit.
As you move through the first unit, refer back to the poster frequently and ask students if they would like to add anything new or revise a previous idea.

Related Posts

Routine 2: Talking Points

Directions

Arrange students in groups of 3 or 4.
Print a copy of the talking points for each group.
As a class, review how each round works. The first time you do this, it might be helpful to also model the process with a fun talking point such as, “A hot dog is a sandwich.”

ROUND 1 – Read the first talking point aloud. Take turns going around the group, with each person saying in turn whether they AGREE, DISAGREE, or are UNSURE about the statement and why. Even if you are unsure, you must state a reason why you are unsure. As each person shares, no one else comments. You are free to change your mind during Round 2 and/or Round 3.

ROUND 2 – Go around the group a second time, with each person saying whether they AGREE, DISAGREE, or are UNSURE about their own statement OR about someone else’s agreement, disagreement, or uncertainty from Round 1. As each person shares, no one else comments. You are free to change your mind again during Round 3.

ROUND 3 – Go around the group a third time to take a tally of AGREE / DISAGREE /UNSURE votes and record that number on your Talking Points sheet. Then, move on to the next talking point.

Sample Student Handout with Third Grade Talking Points

Talking Point	Agree	Disagree	Unsure
Fractions are always less than 1.
A fraction is a number.
We can locate fractions on a number line.
Fractions tell us a size.
One half is always greater than one third.
We can combine fractions.

Sample Math Mindset Prompts

Being good at math means being able to do math problems quickly.
A person is either good at math or bad at math.
I prefer to work on problems that challenge me rather than ones I find easy.
When working in a small group, if one person knows how to solve the problem, they should show the others in their group how to do it.
There is always one best way to do math.
Getting a problem wrong in math means you failed.
Drawing a picture is always helpful when doing math.

Sample Math Content Prompts

5 is the most important number.
The number 146 only has 4 tens.
Fractions are numbers.
When multiplying, the product is always greater than the factors.

Division of fractions is just like division of whole numbers.
The opposite of a number is always a negative number.
It is easier to work with decimals than with fractions.

For any equation with one variable, there is one best way to solve for the variable.
It is easier to work with degrees than with radians.

Related Posts

Math Reflections to Wrap Up the School Year

Leave a reply

At the end of the year, it is always so interesting and insightful when students reflect on what they have learned. In 3rd grade, we asked students to show all of the things they learned about different concepts and list any questions they have. We typically do this for the major work of grade concepts and in this example, we asked about multiplication.

I absolutely loved all of the different ways of showing what they know and REALLY loved that it wasn’t just a list of multiplication facts. We also got a great question about multiplying negative numbers!

I just think about being the 4th grade teacher getting these papers to learn more about the students’ understandings coming into my class next year. How much more valuable would these be than a STAR score?

Happy end of the school year everyone!

Leveraging Digital Tools for Problem Posing

1 Reply

I have blogged a few times about problem posing using print materials and lately I’ve become really interested and excited about the potential for digital tools in this work!

If you are new to problem posing, below are a few slides from Jinfa and my NCSM presentation for background – each image is linked to an associated research paper.

What is problem posing?

Many activities can easily be adapted to provide opportunities for problem posing by removing task questions (left) and replacing it with different prompt options (right).

How can digital tools enhance problem-posing experiences?

Being relatively new to both problem posing and digital lessons, I have learned so much trying things out in math classes this year. As always, the more I learn, the more questions/ideas I have. Below are two digital lessons that involve different flavors of problem posing.

Lesson 1: Our Curious Classroom

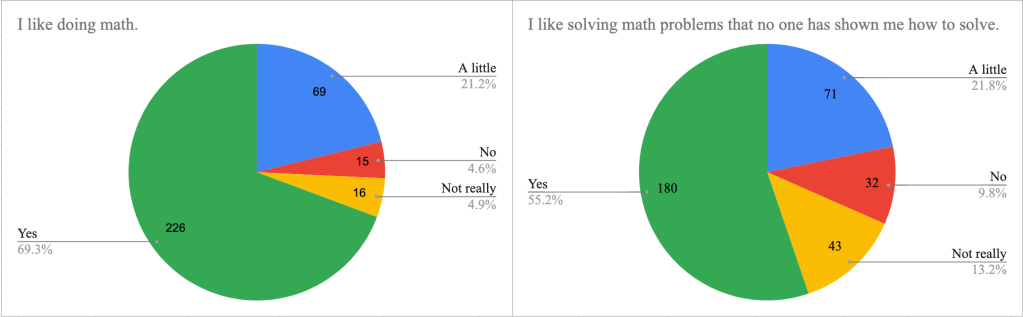
You can click through the lesson screens to see the full flow, but in a nutshell, students answer questions about themselves and explore different data displays.

After answering the first survey question, we asked students for problems they could answer about their class data and recorded their responses (sorry for the blurry image, I had to screenshot from a video clip:).

The students then worked at their table to answer the questions based on their choice of display.

The lesson continues with more survey questions, data display exploration, and ends with students personalizing their own curioso character (see bottom of post for unrelated, cute idea).

Things I learned:

Student responses can be collected and displayed so quickly with digital which saved us more instructional time for posing and solving problems.
The capability to see data displays dynamically change from one to another enhanced the discussion about which display was most helpful to answer the problems and why.
Students were so motivated to answer questions about themselves, learn about their classmates (audio clip below), and ask and answer questions about their own class, not a fictitious one.

“What did you like about the lesson?”

Things I wonder:

While having the teacher record the questions on the board worked perfectly, I wonder if or how younger students might digitally input their own questions w/o wearing headphones for voice to text or having spelling errors that are challenging for others to interpret? Maybe something like a bank of refrigerator magnets to choose from?
During the lesson, could the teacher input student questions onto cards in the Card Sort in Desmos so they could then sort the problems based on structure before solving?

Lesson 2: Puppy Pile

In this lesson, students generate a class collection of animals, are introduced to scaled bar graphs, and create scaled bar graphs. This one has a different problem-posing structure than the the first lesson which was interesting!

In this lesson, students use the Challenge Creator feature. In order to pose their problem to the class, students create their own set of animals (left) and then select a scale and create a bar graph (right).

After submitting their challenge, students then pick up one another’s problems and solve them.

Things I learned:

Students were extremely motivated to create their own problems and solve the problems of others.
This version of problem posing allowed students to have more control over the situation around which they were formulating problems, which they really enjoyed.
Challenge Creator is an amazing tool for repeated practice that is MUCH more engaging than a worksheet of problems.

Things I wonder:

How could this activity structure support or extend the problem posing experience in Lesson 1?
What other K-5 math concepts would be great candidates for a Challenge Creator problem-posing activity?

Final thoughts

I think problem posing is such an important instructional structure whether done in print, digital, or a hybrid of the two. It is important, however, to also consider the math, student motivation, and amount of time students spend engaging in the problem-posing process when choosing the format we use.

I would love to hear about what you try, learn, and wonder whether you try these lessons or adapt other lessons for problem posing!

Unrelated by Adorable Idea…

After Lesson 1, Katie printed out their personalized Curiosos for the wall;)

Making Connections for Deeper Learning

Leave a reply

In 3rd grade, students come to understand fractions as numbers. They count by them and locate them on a number line just like whole numbers. However, once they start operating with fractions in 4th and 5th grade, they tend to set aside everything they understand about whole number operations and treat fractions as numbers with their own set of ‘rules.’ I can think of many reasons why this happens, but my current wondering is how we can create more opportunities for students to make connections between their understanding of whole number and fraction operations.

Why Connections?

So many times I see students not realize all of the wonderful things they know that would be helpful in their new learning. I believe this is because we just don’t spend enough time making connections explicit to support this transfer.

One of my favorite papers on the importance of practicing connections (linked in the citation) describes the ‘why’ so nicely…

“Although there may have been a time when rote learning of facts and procedures was sufficient as an outcome for education, that is certainly not the case today. Anyone with a phone can Google to find facts that they have forgotten. But gaps in thinking and understanding are not easily filled in by Internet searches. Increasingly, we value citizens who can think critically, coordinate different ideas together, solve novel problems, and apply their knowledge in all kinds of situations that do not look like ones they have previously encountered. In short, we want to produce students with deep understanding of the complex domains that constitute the modern knowledge landscape (National Academies of Sciences, Engineering, and Medicine 2018).”

“Studies show that expert knowledge in a domain is generally organized around a small set of core concepts (e.g., Lachner and Nückles 2015) that imbue coherence to even wicked domains. Because they are highly abstract and interconnected with other concepts, core concepts must be learned gradually, over extended periods of time and through extensive practice. As students practice connecting concepts with other concepts, contexts, and representations, these core concepts become more powerful and students’ knowledge becomes more transferable (e.g., Baroody et al. 2007; National Council for Teachers of Mathematics 2000; Rittle-Johnson and Schneider 2015; Rittle-Johnson et al. 2001).”
Fries, L., Son, J.Y., Givvin, K.B. et al. Practicing Connections: A Framework to Guide Instructional Design for Developing Understanding in Complex Domains. Educ Psychol Rev 33, 739–762 (2021).

Subtracting Whole Numbers

In 4th grade, students have been decomposing fractions into sums of fractions with the same denominator and justifying their decompositions. They naturally leveraged their understanding of whole number decomposition, but when we gave them a problem to add or subtract, they quickly looked for a ‘rule’ to find the sum or difference. And, while we want them to generalize these operations, as the numbers get more complex –mixed numbers and unlike denominators – a memorized rule absent understanding doesn’t help students reason about the problem.

The lesson last week had students representing their fraction addition and subtraction on the number line, but that representation was causing some students more angst than support so we decided to use the problems from the lesson, but focus on the connection to whole number operations instead of forcing only the number line on them.

On their whiteboards, we asked them to record all the ways they think about and can represent 13–6=?. We saw a nice mix of ideas like removing items (base 10 blocks), hopping back on a number line, decomposing 6 and subtracting in parts, adding up (relationship to addition), and the algorithm – which made them all chuckle because after ‘borrowing’ it ended up being the same problem.

Connection to Subtracting Fractions

We shared these ideas out, recorded them on the board for reference, and then asked them to erase their whiteboards and do the same thing for 13/5 – 6/5=?. Students shared the methods and representations they used and we discussed how they were like the ones they used for whole numbers. It took no time for someone to say ‘It is exactly the same, just fifths.’ One student wrote it out in words so the discussion of the change in units was perfect.

Applying the Strategies

Next we wanted students to practice a couple of problems, including mixed number subtraction where the first fraction numerator was less than the second. We were excited to see many of the same methods being used and some students really got into showing it multiple ways.

Try it out!

Any 4th and 5th grade teachers out there who want to try this out, I would love to hear what you learn about student thinking and what students learn about important connections in math class!

Small Change, Big Thinking

Leave a reply

Adapting math activities is one of my favorite parts of lesson planning. I love it so much because of the thoughtfulness, curiosity, and creativity involved in even the smallest of changes. In making any change, I have to think about what students know, the math of the activity, how the activity addresses the learning goal, ways students might engage in the activity, and questions to ask students along the way.

Fraction Activity

In this 4th grade activity, students were writing equivalent multiplication equations for a fraction multiplied by a whole number and then discussing the relationship between the different equations. The curriculum activity was good and definitely addressed the learning goal, but there was definitely an opportunity to open it up for more student reasoning and ownership. For example, in its current form, students don’t have the chance to think about which whole numbers would work in their equations or play around with the properties.

Small Change

Adapting doesn’t always require huge lifts. For this activity, all we decided to do was change the prompt to 12/5 = ____ x _____ and ask them to find as many ways as they could to make the equation true. I got so wrapped up in their work and discussions, that I didn’t snag any pictures of that part of the lesson, but after they finished we pulled up polypad and asked them how we could show why they are are all equivalent using the fraction bars. We wanted to be sure they just weren’t proceduralizing it at this point of the unit, so pulling up the fraction bars felt like a nice grounding of the concept. The board looked like this before we erased to make space to circle the other expressions.

Making Connections

At this point, they couldn’t get enough and asked for another fraction to try, so we gave them 16/3. We saw so much great thinking and use of the commutative property when finding the whole number and numerator.

Their excitement alone was the first indicator that allowing more space for their choices was a great idea! And then, as I was walked around, a couple students asked if they could write division equations. Of course I said yes and walked away.

I came back to #7 and #8 on this board:

When I asked how she came up with those equations, she said she used her multiplication equations because multiplication and division are related. I left her with the question of how she might show that division on the fraction bars and class wrapped up. I can’t wait to check back in with her tomorrow to see what she came up with!

Next time you plan a math lesson, I encourage you to think about small tweaks you can make to open it up for more student voice, ownership, and opportunities to think big! And I don’t know if anyone is even talking much about math planning on Twitter (X) anymore, but if you are, I would love to think together about tweaking math activities. So, send some activity pics my way @MathMinds and we can flex our curiosity and creativity muscles in planning together.

-Kristin

Supporting Mathematical Habits of Mind

Leave a reply

“The widespread utility and effectiveness of mathematics come not just from mastering specific skills, topics, and techniques, but more importantly, from developing the ways of thinking—the habits of mind—used to create the results.“
Cuoco, Al & Goldenberg, Paul & Mark, June. (2010).

Math curriculum lessons are often aligned to the Standards of Mathematical Practice. These practices can provide opportunities for students to develop the mathematical habits of mind described by Al Cuoco, Paul Goldenburg, and June Mark.

Mathematical Habits of Mind

Students Should Be Pattern Sniffers
Students Should Be Experimenters
Students Should Be Describers
Students Should Be Tinkerers
Students Should Be Inventors
Students Should Be Visualizers
Students Should Be Conjecturers
Students Should Be Guessers

The thing I love most about these habits of mind is the fact that as I read them, I can picture the math content and activity structures that could provide opportunities for students to develop these habits. I also really like the connectedness of them, where I can easily imagine how one habit leads students to engage in another. And because my favorite Math Practice is SMP7, look for and make use of structure, I am particularly drawn to the habit of conjecturing in math class. Excitingly, last week 5th graders were engaging in a topic that provided a perfect opportunity to conjecture.

Fraction Division

This past week, 5th grade students were dividing unit fractions by whole numbers and whole numbers by unit fractions. If you have ever taught this, you probably immediately picture students overgeneralizing these two different situations. In the vein of answer-getting, they often think the quotient will either always be a whole number OR always be a unit fraction – both including the product of the denominator and whole number in some way. And even though students have engaged in a lot of the habits within this work, it was with the two situation types separately.

To address the overgeneralization, we wanted them to engage in mix of the situation types in order to compare them. We launched with the following 2 problems, purposefully choosing the same numbers to elicit the difference in what is happening in the situation and the resulting quotients.

Student Thinking

As anticipated, we saw wonderful diagrams that generally matched each situation, but we could tell by the shading and erased work on Situation B that students were thinking that because they were working with fractions, their answer had to be a fraction.

We focused our discussion on the questions, “Where is 1 cake in your diagram?”, “Where are the people in your diagram?”, “Where are the servings in your diagram?”, and “Where is your answer in the diagram?”. Through those questions we saw a lot of labeling revisions to their work to make it clearer.

Mathematicians Talk Small and Think Big

“The simplest problems and situations often turn into applications for deep mathematical theories; conversely, elaborate branches of mathematics often develop in attempts to solve problems that are quite simple to state.”
Cuoco, Al & Goldenberg, Paul & Mark, June. (2010)

While the discussion was productive and we saw a ton of sense-making, visualizing, describing, and revision, I was left wondering how this moment transfers to the next time a student engages in one of these division situations.

I love this idea of tinkering around with smaller ideas to conjecture about larger ideas as a great way for students to deeply understand a concept and be able to transfer their understanding to the next time they engage in that concept.

So, for the tables done their discussions early, I asked them to write things they think are true about the division and lingering questions they might have. Here are a couple examples:

Next Steps

The question I am always left with after students have such amazing insights and questions is, ‘How do I keep this math conversation alive?’ With the pacing of curriculum, it can be challenging to dig into each of these moments for an extended period, so we need ways to let this thinking extend across the year.

One thing we could do is ask students if we can launch the next class period with their ideas. For example, I might ask the first student if I could post, “The order matters in division.’ at the start of class the next day and have the class discuss if they think that will always be true and why. This would be a great way to elicit the difference in quotients when we divide a whole number by a fraction and vice versa.

Another option that I used in my classroom, was posting the ideas on what I called a Class Claim wall. When students make a claim or conjecture, we posted them on the wall and then anyone could revisit them at any point and time.

I think both of these options are a wonderful way for students to continually think small and big about concepts while allowing us the opportunity to communicate to them that just because a curriculum unit of study wraps up, the learning about that concept continues.

-Kristin

If you want to read a bit more about claims and conjectures, I was kind of obsessed with it when I was teaching and blogged a lot:

Developing Claims – Rectangles With Equal Perimeters

Geometry Is Worth The Extra Time…

The Meaning of Subtraction