Category Archives: multiplication of fractions

Small Change, Big Thinking

Fraction Activity

In this 4th grade activity, students were writing equivalent multiplication equations for a fraction multiplied by a whole number and then discussing the relationship between the different equations. The curriculum activity was good and definitely addressed the learning goal, but there was definitely an opportunity to open it up for more student reasoning and ownership. For example, in its current form, students don’t have the chance to think about which whole numbers would work in their equations or play around with the properties.

Small Change

Adapting doesn’t always require huge lifts. For this activity, all we decided to do was change the prompt to 12/5 = ____ x _____ and ask them to find as many ways as they could to make the equation true. I got so wrapped up in their work and discussions, that I didn’t snag any pictures of that part of the lesson, but after they finished we pulled up polypad and asked them how we could show why they are are all equivalent using the fraction bars. We wanted to be sure they just weren’t proceduralizing it at this point of the unit, so pulling up the fraction bars felt like a nice grounding of the concept. The board looked like this before we erased to make space to circle the other expressions.

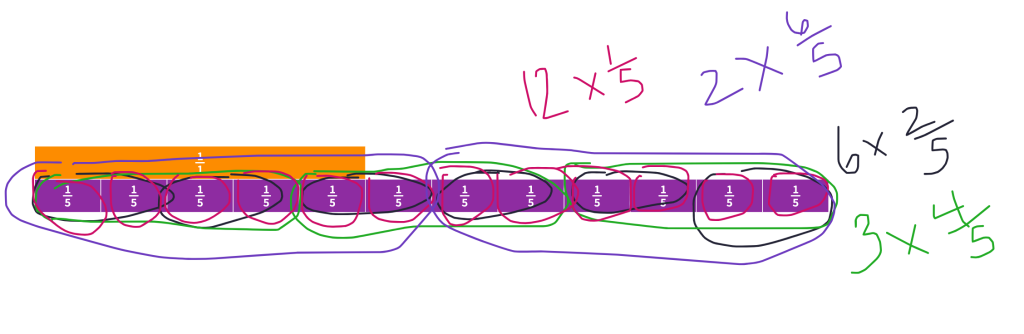
Making Connections

At this point, they couldn’t get enough and asked for another fraction to try, so we gave them 16/3. We saw so much great thinking and use of the commutative property when finding the whole number and numerator.

Their excitement alone was the first indicator that allowing more space for their choices was a great idea! And then, as I was walked around, a couple students asked if they could write division equations. Of course I said yes and walked away.

I came back to #7 and #8 on this board:

When I asked how she came up with those equations, she said she used her multiplication equations because multiplication and division are related. I left her with the question of how she might show that division on the fraction bars and class wrapped up. I can’t wait to check back in with her tomorrow to see what she came up with!

Next time you plan a math lesson, I encourage you to think about small tweaks you can make to open it up for more student voice, ownership, and opportunities to think big! And I don’t know if anyone is even talking much about math planning on Twitter (X) anymore, but if you are, I would love to think together about tweaking math activities. So, send some activity pics my way @MathMinds and we can flex our curiosity and creativity muscles in planning together.

-Kristin

Dot Image with Halves

2 Replies

Yesterday, I was thinking about some new number routines for the 4th and 5th graders who will soon be in their fraction units. I wanted to find something that both grade levels could engage in so the teachers could try them out and have a common talking point when we met to discuss what we learned about student thinking. I tweeted it out and didn’t want to lose all of the great thoughts so I going to compile them here!

This was the image I created:

Screen Shot 2016-10-21 at 1.46.43 PM.png

Before launching this with the students, I thought the teacher would establish that a full circle was 1 and ask the question we typically use with our dot images, which is

How many dots do you see and how do you see them?

I thought there could be a variety of responses, but I was most anticipating these two responses:

I know two halves make 1 and so the first row is 3. There are 4 rows so 4 x 3 =12.
I know two halves make 1, so the first column is 2. There are 6 columns so 6 x 2 =12.

I knew questioning would be important to move from those descriptions to what the equation would look like and imagined we would get to some like this:

6 x 1/2 x 4 = 12
4 x 1/2 x 6 = 12

Other interesting things I am now thinking about thanks to others on Twitter:

You could just start with ambiguous “How many?” Some may count half circles, some full. I’d love to listen in.

— Michael Fenton (@mjfenton) October 22, 2016

Why am I stuck on dots? Circles makes so much more sense!

Yes, why not leave it completely open,not tell them that circle is 1 and talk about the unit?

Screen Shot 2016-10-22 at 5.06.44 PM.png

It is funny that the same image conjures up different student responses, I always love that! I had not anticipate half of an array. I also love the idea of messing around with quarters here!

Screen Shot 2016-10-22 at 5.09.25 PM.png

Awesome to have them do some scaling of the dots to find how many are there? And then I can see them saying it is half of the array like Michael suggested once it is uncovered!

Screen Shot 2016-10-22 at 5.10.57 PM.png

I like the idea of moving them around however the cutting and tearing thing never goes well in my room!! I do love changing the value of the whole a lot!

Screen Shot 2016-10-22 at 5.12.19 PM.png

I debated this part a lot when I was making it! I thought for the 1st one, a whole number would be best and then move to non!

There is the running list so far! Add away in the comments!

5th Grade Fraction Multiplication

2 Replies

Yesterday, in my planning, I was bouncing around between a couple of ideas for the lessons I was teaching today. I decided to go with this Illustrative task that was the basis for the lesson study project I did last year with The Teaching Channel and Illustrative. I though it would be a great formative assessment as students move from thinking about fraction of a fraction on a fraction bar to an area model using a square unit.

I opened with a choral count in which the students counted by 3/4. I played around with ending each row on a whole number (12/4, 24/4, 36/4…etc) or ending on something not as “nice.” I opted for the second, but in hindsight, probably should have gone with the first. I really wanted more conversation around when the whole number occurred and why and possibly the distributive property (4 x 3/4) + (1 x 3/4) = 15/4, but not as obvious as I felt the first option made it, but it didn’t happen. The count looked like this (I didn’t get a chance to take a pic of the board):

FullSizeRender 37.jpg

I asked students what they noticed and I got a variety of responses. I got many variations of equations such as 3/4 + 6/4 = 9/4 and 12 x 3/4 = 36/4, and with each one, I asked how we could show that within the count. One student said she could see 20 x 3/4 =60/4 in the count. Just when I thought she was going to explain by saying we counted by 3/4 twenty times, she surprised me in her wording. She said, “I knew the count was a 4 by 5 array, which is 20 numbers and then each one was 3/4, so I got 60/4.” This struck me different than the skip counting or repeated addition of 3/4 that others were doing and reminded me a a bit of this diagram from the learning progressions:

Screen Shot 2015-12-06 at 3.32.17 PM.png

I think it was the way she described the size of each number in the count as 3/4 that drew me to this diagram.

Next I gave them the task to engage in alone for 5 minutes before I let them move into group work. I was really impressed by the way they jumped right in and easily could find 1/3 of 1/4. I was not surprised that many ignored the “square pan” piece and went with fraction bars. Much of the work looked like this, cut vertically: IMG_1262 (1).jpg

While there were also quite a few students who quartered it by cutting vertically and horizontally in half and then splitting that quarter into thirds:

This is something for me to think (learn) more about because if we are thinking area model, the dimensions of the piece, to me, looks like 1/2 x 1/6. That seems like it could be problematic to me when the square has dimensions in units of length.

Another interesting thing that always comes up in this work is the difference between dividing by a fraction and dividing it up into fractional parts. I saw those equations sneaking there way in like this…

That will be something to keep in mind in future lessons. What it means to divide by a number versus divide into parts? Is it different when we are thinking about whole numbers versus fractions? Cool convos to be had around that!

There was one student who was not working with the original whole in her work. She was working with the 1/4 in the first part and then the 1/2 in the second part. When I asked her about how she was determining 12ths, she said it was just like her phone, she took the whole thing and just zoomed in (she did the fingers swipes as you would do on your phone) on the part she needed.

There was some really great proportional reasoning going on with the cost of the cornbread pieces. When the pan price changed from $12 to $24, $6, and $18, student used great reasoning in relation to $12. In the example above you can see that work as well as here:

I left them with a question about the denominator, why is not ending up in any of the denominators we are using the problem? I only had a chance to snap one pic before I headed to another classroom.

Lots of great stuff to keep in mind and I think comparing the ways in which the students divided the models would be a really interesting conversation. Then after they move to an area work, I wonder if it would be great to bring that back for a comparison.

Also, I forgot to add that the substitute who was in for Leigh today was so incredible about taking notes and talking to the students because he was going to be in charge of teaching this same lesson to the next math class that came in. He said he learned so much and I thought this could be such a powerful way to have substitutes involved in learning more about the way in which math is taught.

~Kristin

Planning K-5, literally

5 Replies

Tomorrow I have the opportunity to teach a Kindergarten, 2nd and 5th grade class! It is so exciting and interesting to be thinking across all of the grade levels in one day of lesson planning! The most interesting part for me, in thinking through this, is the connections across all of the grades. There is so much potential for conjecture and claim-making supported by their development of proofs.

Background: The 5th and 2nd grade teachers are out at a state math teacher leader meeting so I am teaching instead of the substitute. The kindergarten teacher and I will be teaching it together. I have met with each teacher to chat about where they are within their units and what they have been seeing students do within the current work. I invited teachers both at those grade levels and at other grade levels to pop in if they have the time. I thought it would be great having more people to reflect with after the lessons!

5th Grade: They have just started working with finding a fraction of a fraction using bar models. The initial work is unit fraction of a unit fraction and then moves to non-unit. (My post on that from a couple of years ago on this work, I wish I had done that better, so here is a chance to try something new;) Leigh, the teacher, says they have been really successful in partitioning the bars and arriving at the correct answer. I am thinking about starting with a number routine of either a choral count or a number talk string like 1/2 of 12 = __ of 24… As far as the lesson, I could continue work with this and have students look at noticings after and explore them deeper.They have done these noticings with whole number times a fraction or mixed number, so this could be a revisiting of similarities or differences. OR I could do this cornbread task as a formative assessment as the next piece they will move into is an area model. It may be really helpful for Leigh to see how they are thinking about this before they jump into the work. This is my least planned because I keep bouncing all around with ideas.

2nd Grade: They have been working with even and odd numbers and counting by groups of 2’s, 5’s, and 10’s. All of this work is within contexts of break a group of students into equal teams or everyone having a partner. Tara, the classroom teacher, said the students are really great at determining whether a number is odd or even, however when asked how many would be on each team, a lot of students struggle. They are great if they know a related double fact, however if they don’t they resort to “passing out” by tallies or drawing the picture and physically dividing the number of things in half. For example, if they do not know 11+11 is 22, then finding the number of on each team become passing out 22 things into two groups to find 11. While they are successful in this, Tara and I were wondering why they do not say 10+10=20 and 1+1=2 so 11+11=22. They are able to add 11 and 11 but unable to decompose it as fluently.

In thinking about this, I am inclined to want to connect that addition to halving. I am thinking a counting collection would be fabulous for this. Give students a collection of things to count. Share how we counted them because I am positive they will not count them by 1’s given a large set. We can share as a whole group, record ways in which we counted and determined if our number was even or odd. Then, put the collection back together, switch with a partnering team and then split the collection into two groups. The share would be, “Could you make two equal groups?” “Was your number even or odd? How did you know?” Record strategies. Ask for noticings/wonderings about how they counted and how they divided into two groups.

Kindergarten: The students in this class have been doing a lot of work with ten frames, dot images, counting jars, etc and having students counting and adding to compose a number. They have just begun working on decomposition of number so I immediately thought about the mice activity in Thinking Mathematically. Linda, the teacher, and I planned to do this activity with the students. In preparation, we read NCTM TCM’s article by Zachary M. Champagne, Robert Schoen, and Claire M. Riddell, Variations in Both Addends Unknown Problems. We are going to use 6 bunnies and see how students show all of the ways the bunnies can be inside and outside in a pen. Instead of just giving a context, I was imagining that the students may need a visual of the rabbit pen so I created this image to launch with a quick notice and wonder:

Screen Shot 2015-12-06 at 9.51.28 AM.png

We will then let the students work on finding the different ways in partners and then come back for a whole group share and record the ideas on the board. We are really looking to see two things….1-how they organize their information and 2- the strategies they use. The students will do a notice/wonder about the recorded information. If there is time it would be great to see if students, when given a different number, would apply any of the strategies and/or organizational tools shared.

Going for a run to think through this a bit more! Would love any thoughts/suggestions, as always!

~Kristin

Listening Carefully to Student Thinking

7 Replies

Recently, I have been reviewing a new “CCSS-Aligned” middle school curriculum and find myself completely frustrated with the overabundance of scaffolding and lack of student thinking required on every assignment. Not having the days/weeks it would take for teachers to engage in the mathematics as both learners and teachers, I needed a short, powerful way to show that this is not how students should experience/learn mathematics.

As I looked at the fraction page like this, my thought was “Why just two ways?” quickly followed by “Why those two ways?” quickly followed by “My students are doing this now, flexibly.”

Right then, I realized the perfect proof of why NOT to do this, was the work my students already do when given the freedom to reason about a problem and do more than just procedurally compute an answer. So, I put the proof in their hands. I simply asked them to solve 2/5 x 7/10 as many ways as they could. Some got creative after a couple of ways, and by no means am I saying some of these are “efficient,” but they show so much flexibility.

This felt perfect. Why would we want to miss out on all of the great conversations that can happen around this work by making them answer in just 2 ways, and more specifically, those 2 ways they show you how to do…step-by-step?

and THEN this happened which validated my thoughts even further and instantly made me reflect on my friend Christopher’s talk at ShadowCon (video coming soon) around listening carefully to student thinking…

The students were working on 2/5 x 7/10 as I was walking around the room observing their work. I glanced over a student’s shoulder and saw “Doubling and Halving” written on her paper with the correct answer. Assuming it was doubling/halving in the sense of doubling one factor and halving another factor, I was excited to see the use of the strategy.

I asked her how she did it, she said, “I double/halved” and I was about to move on to get ready for our sharing. When I glanced down, however, it was not at all like I had imagined. I asked her to explain further…“I halved this numerator and doubled this denominator [points to 2/5] then I doubled this numerator and halved this denominator [points to 7/10].”. Ok, now THIS is much different than I thought!!

I had her share, and others immediately said they had double/halved also but did not get those fractions to multiply and wondered if that worked every time (I love that they ask that now:). I let them play around with it for a bit but since we had some division work to do I told them to keep thinking about that and we will revisit it tomorrow. By the end of the next class period, I had a student come up and say, “She didn’t double/half really, she quadrupled/fourthed.” I asked him to write down his explanation for me because it was lovely.

So glad I listened carefully and didn’t makes assumptions on her understandings because how amazing is this work? I am also so glad that I can appreciate a curriculum that allows for these reasonings and conversations to happen.

-Kristin

Collaboration As Key Work

Commutativity in Fraction Multiplication

2 Replies

Think about these two expressions…

2/3 x 6 6 x 2/3

Do you think differently about each?

Does your solution approach change?

I had not really given this much thought because we do both in 5th grade, multiply a fraction by a whole number and whole number by a fraction. However, recently, when working with a group of 4th grade teachers and looking more closely at the standards and my curriculum, I am beginning to see a distinct difference. I now look at each expression from a different perspective. Not that both ideas do not arise at multiple grade levels in some form or another, but it is so interesting to me as to which thinking would come before the other.

Let’s first look at the standards…

4th Grade:

5th Grade:

Interesting. For me, taking a fraction of a group feels more “natural” and intuitive than multiplying a whole number by a fraction, however in the learning trajectory of multiplication and building of unit fractions composing a whole, the multiplication of a whole by a fraction feels like the natural next step.

For our upcoming Illustrative Mathematics professional development, I was collecting work samples for the following problem (thanks Jody:)

“Presley is wrapping 6 packages. Each package needs 2/3 of a yard of ribbon. How much ribbon will she use for wrapping the 6 packages?”

As anticipated, I received a wide variety of solutions to arrive at 4 yards of ribbon. Here are just a few examples in what I think is the progression I expect (some of them got finished quickly and opted to show a few ways to solve).

They all finished fairly quickly and as I was walking around I thought it was really interesting to see such a variety in the equations they used to represent the problem. We came together as a whole group and I asked them for the equations they thought best represented the problem. The most common answers were: 2/3 x 6 = 4, 6 x 2/3= 4 and 2/3 + 2/3 + 2/3 + 2/3 + 2/3 + 2/3= 12/3 = 4.

I asked them if there was a difference between the equations and there was a unanimous “No” because they mean the same thing. “They all get 4.” In my head I was very excited that commutativity was something they see when finding a solution, but I was also curious if it worked the same in the opposite direction. I asked if we could narrow it down to two equations and they all agreed that the repeated addition was the same as 6 x 2/3 because it was “six groups of 2/3.” Interesting, so they see that in the numeric representation but not contextually?

I then asked them to write 6 x 2/3 and 2/3 x 6 on the top of their journal page and think about them without the previous context. I posed, “If I gave you these two problems to solve, would you think about them the same way? Do you think about them differently?” I was curious to hear their thoughts on the commutativity.

The conversation after was so great and interesting! There is a difference when going from number to context, however when put in context, I think students use whatever strategy is easiest for them to arrive at the answer. Is this what is truly meant by contextualizing and decontexualizing in the SMPs?

To further intrigue me, I went and pulled a few fourth graders to interview during my planning period. It was so interesting that they saw this as a whole number times a fraction because it was “six 2/3’s.” Their connection to multiplication and “groups of” was evident. I did love how they did 3 of the 2/3s first to get 2 and then doubled that to get 4.

This 4th grader was the most interesting..

She solved it as 2/3 of 6 and arrived at 4. I asked her if she could write an equation for the problem she solved and she wrote 2/3 of 6 = 4. Completely because I am so nosy, I asked her to write 6 x 2/3 under that. I asked how she thought about that problem? Would she solve it the same? She said, “No, that is 6 of the 2/3’s so I have to multiply the 2 and 3 by 6.” She proceeded and ended with 12/18. She saw the numerator and denominator as numbers in and of themselves and used the distributive property to arrive at her answer instead of thinking about the 2/3 as a number. This was something I had never thought of before! I wish I had more time with her because I SO wanted to ask if that makes sense, but since my planning runs into dismissal, she had to get back to class! Argh!

This progression (to me) now seems to be more about building on student’s understanding of multiplication then about what is more intuitive for students to do. That is such a revelation to me. In second and third grade students do so much in “sharing” situations, that I had assumed it was en route to this skill of taking a fraction of a number when in fact it is more about the operations. It builds multiplication and division. Those operations then progress from operations with whole numbers to operations with fractions and from there students start to build deeper understandings of the properties of operations.

This is of course, all my interpretation based on my experiences and perspective of the student work, but how awesome! I cannot wait to share this with the 4th grade teachers along with the video of the kids chatting with me about this, awesome stuff!!

-Kristin

“Is this really just multiplication?”

7 Replies

After a couple of weeks working with problems in which they were taking a fraction of a fraction, fraction of a mixed number, the students made some conjectures about the problems.

We went through each one, proved, disproved and refined them when finally one student just asked..

“Ok, isn’t this really just multiplication?”

I knew he just wanted an answer, but that was not going to happen. 🙂 Since we have been doing a lot of multiplication number talks, I thought I would see if I could make a connection to whole number operations.I said, “Well, if it is multiplication, do you think the strategies on our anchor chart should work for the fractions too?” We made the anchor chart as strategies arose in our number talks. I put 2 1/4 x 1/2 on the board and said, “Try it out.”

They worked in groups and came up with some pretty amazing stuff…(A couple students chose to try a different problem, so the sampling below may be a mix)

We are going to share some strategies tomorrow since the rest of the class period consisted of them “arguing” about fraction multiplication. It made my day when one of the girls was leaving my class and said to her friend, “That was so fun!”

Wait, fractions fun?? LOVE IT!

-Kristin