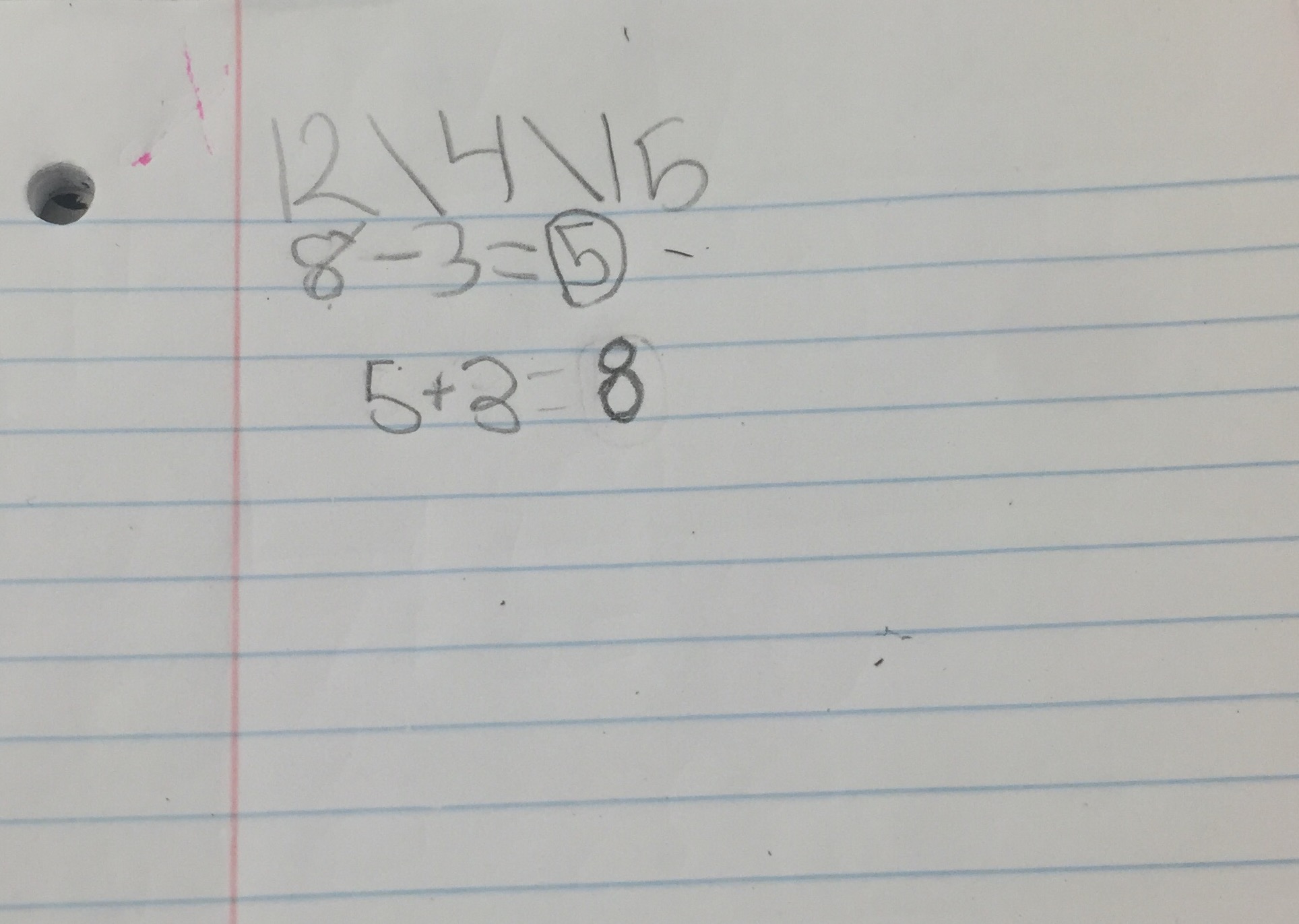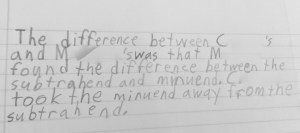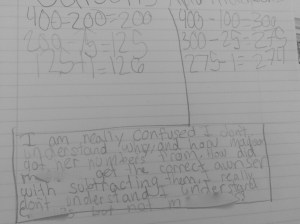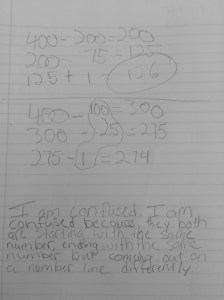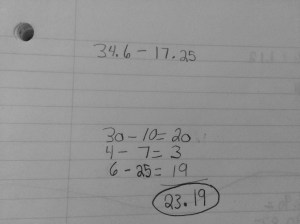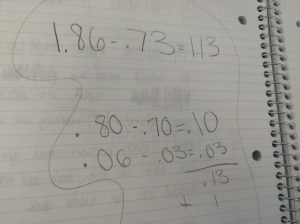Category Archives: Subtraction

Making Connections for Deeper Learning

Leave a reply

In 3rd grade, students come to understand fractions as numbers. They count by them and locate them on a number line just like whole numbers. However, once they start operating with fractions in 4th and 5th grade, they tend to set aside everything they understand about whole number operations and treat fractions as numbers with their own set of ‘rules.’ I can think of many reasons why this happens, but my current wondering is how we can create more opportunities for students to make connections between their understanding of whole number and fraction operations.

Why Connections?

So many times I see students not realize all of the wonderful things they know that would be helpful in their new learning. I believe this is because we just don’t spend enough time making connections explicit to support this transfer.

One of my favorite papers on the importance of practicing connections (linked in the citation) describes the ‘why’ so nicely…

“Although there may have been a time when rote learning of facts and procedures was sufficient as an outcome for education, that is certainly not the case today. Anyone with a phone can Google to find facts that they have forgotten. But gaps in thinking and understanding are not easily filled in by Internet searches. Increasingly, we value citizens who can think critically, coordinate different ideas together, solve novel problems, and apply their knowledge in all kinds of situations that do not look like ones they have previously encountered. In short, we want to produce students with deep understanding of the complex domains that constitute the modern knowledge landscape (National Academies of Sciences, Engineering, and Medicine 2018).”

“Studies show that expert knowledge in a domain is generally organized around a small set of core concepts (e.g., Lachner and Nückles 2015) that imbue coherence to even wicked domains. Because they are highly abstract and interconnected with other concepts, core concepts must be learned gradually, over extended periods of time and through extensive practice. As students practice connecting concepts with other concepts, contexts, and representations, these core concepts become more powerful and students’ knowledge becomes more transferable (e.g., Baroody et al. 2007; National Council for Teachers of Mathematics 2000; Rittle-Johnson and Schneider 2015; Rittle-Johnson et al. 2001).”

Fries, L., Son, J.Y., Givvin, K.B. et al. Practicing Connections: A Framework to Guide Instructional Design for Developing Understanding in Complex Domains. Educ Psychol Rev 33, 739–762 (2021).

Subtracting Whole Numbers

In 4th grade, students have been decomposing fractions into sums of fractions with the same denominator and justifying their decompositions. They naturally leveraged their understanding of whole number decomposition, but when we gave them a problem to add or subtract, they quickly looked for a ‘rule’ to find the sum or difference. And, while we want them to generalize these operations, as the numbers get more complex –mixed numbers and unlike denominators – a memorized rule absent understanding doesn’t help students reason about the problem.

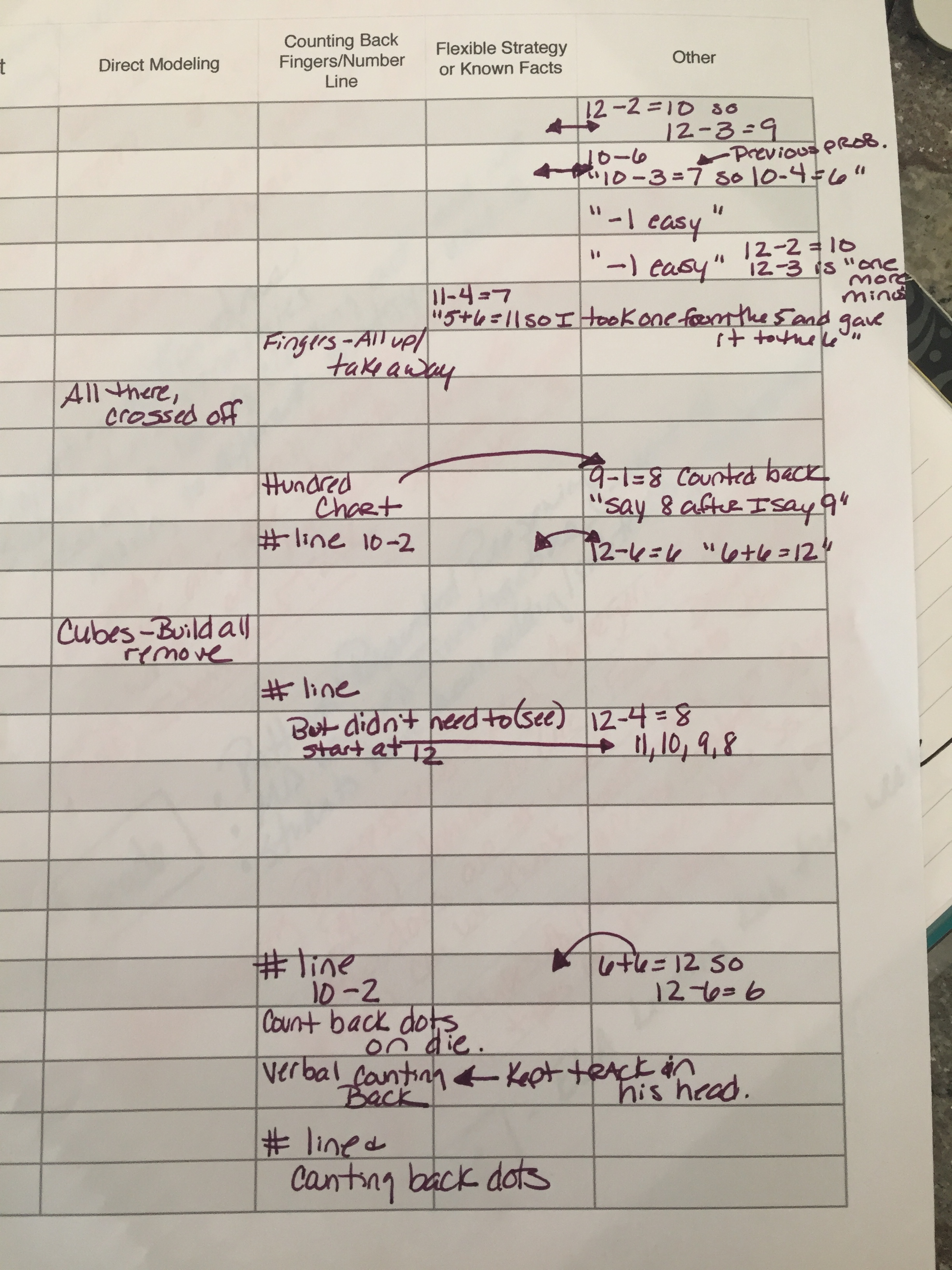
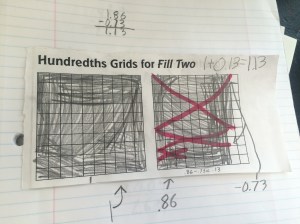
The lesson last week had students representing their fraction addition and subtraction on the number line, but that representation was causing some students more angst than support so we decided to use the problems from the lesson, but focus on the connection to whole number operations instead of forcing only the number line on them.

On their whiteboards, we asked them to record all the ways they think about and can represent 13–6=?. We saw a nice mix of ideas like removing items (base 10 blocks), hopping back on a number line, decomposing 6 and subtracting in parts, adding up (relationship to addition), and the algorithm – which made them all chuckle because after ‘borrowing’ it ended up being the same problem.

Connection to Subtracting Fractions

We shared these ideas out, recorded them on the board for reference, and then asked them to erase their whiteboards and do the same thing for 13/5 – 6/5=?. Students shared the methods and representations they used and we discussed how they were like the ones they used for whole numbers. It took no time for someone to say ‘It is exactly the same, just fifths.’ One student wrote it out in words so the discussion of the change in units was perfect.

Applying the Strategies

Next we wanted students to practice a couple of problems, including mixed number subtraction where the first fraction numerator was less than the second. We were excited to see many of the same methods being used and some students really got into showing it multiple ways.

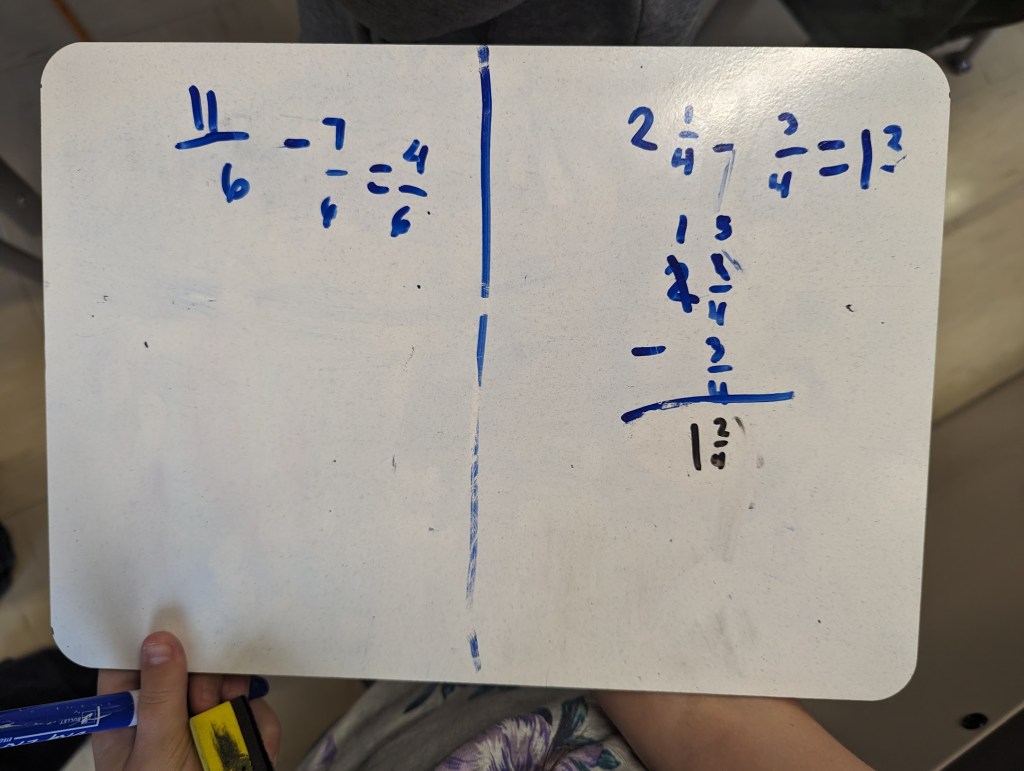
Try it out!

Any 4th and 5th grade teachers out there who want to try this out, I would love to hear what you learn about student thinking and what students learn about important connections in math class!

Number Talk: Which Numbers Are Helpful?

Leave a reply

I think Number Talks are such a powerful routine in developing students’ fluency and flexibility with operations, but maybe not for the reason most think. One of the most highlighted purposes of a Number Talk is the ability to elicit multiple strategies for the same problem, however, an even more important goal for me during a Number Talk is for students to think about the numbers they are working with before they begin solving. And then, as they go through their solution path, think about what numbers are helpful in that process and why.

The struggle with trying to dig deeper into that thinking is simply, time. If the opportunity arises, I ask students about their number choices during the Talk but often students just end up re-explaining their entire strategy without really touching on number choices. Not to mention the other 20ish students start losing interest if they take too long. I do think it is a particularly tough question if students are not used to thinking about it and when the thinking happens so quickly in their head, they don’t realize why they made particular choices.

Last week in 2nd grade I did a Number Talk with two problems, one addition and one subtraction. During the addition talk, I noticed students using a lot of great decomposition to make friendly numbers (the term they use to describe 10’s and 100’s).

IMG_4374

During the subtraction problem, I saw the same use of friendly numbers, however in this one I actually got 100 as an answer. My assumption was because the student knew he was using 100 instead of 98, but got stuck there so went with 100 as the answer. I was really impressed to see so many strategies for this problem since subtraction is usually the operation teachers and I talk endlessly about in terms of where students struggle. I find myself blogging on and on about subtraction all of the time!

IMG_4373

When the Number Talk ended, I looked at the board and thought if my goal was to elicit a lot of strategies, then I was done – goal met. However, I chose the numbers in each problem for a particular reason  and wanted students to dig more into their number choices.

This is where I find math journals to be so amazing. They allow me to continue the conversation with students even after the Number Talk is finished.

I went back to the 100, circled it and told the class that I noticed this number came up a lot in both of our problems today. I asked them to think about why and then go back to their journal to write some other problems where 100 would be helpful.

Some used 100 as a number they were trying to get to, like in this example below. I really liked the number line and the equations that both show getting to the 100, but in two different ways.

IMG_4434

This student got to 100 in two different ways also. I thought this was such a clear explanation of how he decomposed the numbers to also use 10’s toward the end of their process as well.

IMG_4435

This student used the 100 in so many ways it was awesome! She got to 100, subtracted by 100 and adjusted the answer, and then added up to get to 100.

IMG_4428

While the majority of the students chose to subtract a number in the 90’s, this student did not which I find so incredibly interesting. I would love to talk to him more about his number choices!

IMG_4432

I didn’t give a clear direction on which operation I wanted them to use, so while most students chose subtraction because that was the problem we ended on, this one played around with both, with the same numbers. I would love to ask this student if 100 was helpful in the same or different way for the two problems.

IMG_4433

As I said earlier, this is a really tough thing for students to think about because it is looking deeper into their choices and in this case apply it to a new set of numbers. This group was definitely up for the challenge and while I love all of the work above, these two samples are so amazing in showing the perseverance of this group.

In this one, you can see the student started solving the problem and got stuck so she drew lines around it and went on to subtract 10’s until she ran out of time. I love this so much.

FullSizeRender 7

This student has so much interesting work. It looks as if he started with an addition problem involving 84, started adding, then changed it to subtraction and got stuck.

IMG_4436

This is what I call continuing the conversation. They wrote me notes to let me know Hey, I am not done here yet and I am trying super hard even though there are mistakes here. That is so powerful for our learners. So while there was no “right” answer to my prompt, I got a glimpse into what each student was thinking after the Number Talk which is often hard to do during the whole-group discussion.

If you want to check out how I use journals with other Number Routines, they are in the side panel of all of my videos on Teaching Channel. 

Adding & Subtracting: Tools and Representations

11 Replies

There is always a lot of talk about students using an algorithm, process or set of rules, for addition and subtraction. Whether talking about “any algorithm” or “the algorithm,” I am certain, in most cases, people are talking about a process that is absent of tools such as a 100 charts, number lines or base ten blocks. But, what happens when we see the tool becoming an algorithm in and of itself? Can moving left or right on a number line, making jumps of 10s and 1s, writing problems vertically, or jumping rows and columns become an algorithm where students lose sight of the numbers themselves because the process is one more thing to learn?

This was the exact conversation I had yesterday with two 3rd grade teachers as I was leaving school. The students had been playing a game called Capture 5 and struggled making various jumps on the 100 chart. The teacher, understandably, was concerned students were confused about adding and subtracting tens and ones. After more conversation, we began to wonder if the students saw the 100 chart as a set of rules to follow in order to add and subtract instead of a place to look for patterns and structure as we add and subtract. Were they getting caught up in the left, right, up, down movement and losing sight of what was actually happening to the number?

As I thought more about it last night, I wondered about other tools and representations  students learn that could easily turn themselves into an unhelpful set of procedures. I also wondered how often we make connections between these tools and representations explicit. Like, when is one helpful over another? How are they the same? How are they different?

I emailed the teacher my notes (below) and we decided we would try this out this morning.

Scannable Document on Sep 27, 2016, 7_06_18 PM.png

If you can’t interpret from my notes, the plan was to have each student in a group using a different tool or representation as I called out a series of operations to carry out. After the series of addition and subtraction, they compared their answers and discussed any differences. They rotated seats after each series so they had a chance to try out each of the roles.

We came back together to discuss their favorite one. The recording is below…what do I have against writing horizontally, really?? I found this entire conversation SO incredibly interesting!

  • They found the base ten blocks to be “low stress” because they were easy to count, move and trade, but did agree that bigger numbers would be really hard with them because there would be too many.
  • They really did not like adding and subtracting on the number line with multiple jumps. It got messy.
  • They liked mental math because there was nothing (tool) to distract them and they could focus but they didn’t like that you couldn’t check your answer.
  • The 100 chart’s only perk was they didn’t have to write the numbers in, they were already there for them.
  • I really loved that they mentioned the equations were they only way they could track their work. So if someone in their group messed up, the equation person was the only one that could help them retrace their steps easily.
    img_3048

 

 

 

 

 

 

 

 

 

I am not sure what I learned today, I am still thinking a lot about this. I know that I loved having them compare the tools and representations and that the teacher felt much better about their ability to add 10s and 1s. I feel like there are so many other cools things to do here, but my brain is fried today so that will have to wait!:)

 

 

 

 

1st Grade: 1st Day of Subtraction

Leave a reply

 

This week, I planned and taught with Kala in her her 1st Grade classroom! It was the students first day of subtraction in the official “take away context type of work”sense, so it was really exciting to see what they would do with it. During our planning, Kala discussed ways in which she anticipated students would solve the problems and we thought about the framework below that is also presented in the Investigation’s Teacher Notes for that unit.

IMG_1136

Since it was their first day with subtraction, we wanted to be sure to capture their strategies as clearly as possible to help in planning future lessons. To do this, we designed a quick table with the following headings that we planned on jotting notes about the students’ work on as the lesson progressed.Screen Shot 2015-12-05 at 12.46.32 PM.png

The lesson was supposed to open with giving students the following problem:

Max had 9 toy cars. His friend Rosa came over to play with him. Max gave 3 of the cars to Rosa to play with. How many cars did Max have then?

We decided to make this a Notice/Wonder to really allow students to think about what is happening in the context, over focusing on the numbers. So, instead, Kala posed this (we changed the names from above on accident):

David had some toy cars. One day his friend Max came over to play with him and David gave Max some of his cars.

Right away, they began to exclaim, “That was a short story!” As they shared, Kala recorded their noticings and wonderings. The very first notice was about not knowing how many David gave to Max because it said “some.” On the very last notice, the words subtract and minus came out. She couldn’t quite pronounce subtraction so she went with “minus” for her notice. She said David was a minus because he gave some, but Max was a plus because he got some. I loved that way of thinking and had not expected that at all! We then said we were going to answer some of their wonders….David had 9 and he gave Max 3. Then, like a Number Talk, they gave a thumbs up when they had an answer and we shared as a class. Kala and I just continually asked, how did you decide on the 9? Why did you do that with the 3? Where was that in the story? We decided not to write these strategies down because we didn’t want to influence their work during Roll and Record. We wanted to see where they were in their own thinking.

FullSizeRender 30

I then put up the game board for Roll and Record and we talked about how this was the same and different than the Roll and Record they have been playing with addition. They did notice that this board started at 1 instead of 2 and ended at 11 instead of 12. This will be something I would love to have them thinking about more in later lessons…why is this board this way? We played a few practice rounds of rolling a number cube, taking away the number we rolled on the second die, sharing how we subtracted the two numbers and recording it on our sheet.

They then went back to their seats and played with a partner. They had cubes, number lines, and 100 boards available if they chose to use them. These are a few pics I could snap before the game boards were erased.

 

As they played, Kala and I both walked around with our sheets and recorded the strategies we saw happening around the room. I was really amazed at the thinking in so many ways! I could tell they were comfortable using a variety of tools and by the way they could explain their thinking, it was obvious they were very used to doing that as well. This was my completed sheet at the end of the period. There were a couple of students I missed and a couple were absent, but between Kala and I, we had a really great picture of where the students were in their thinking. I was really surprised I only saw a few directly modeling the subtraction. The arrows were from me just starting to write their thinking and forgetting to put it in the appropriate column!

IMG_1226

After they finished playing, we decided to give them the original problem context with two different numbers (8 and 5) to see if they could create a written response of how they solved the problem as well as they were able to verbally explain to us. We did this because Kala had mentioned during our planning that she often sees them resort to drawing and crossing out when asked to show their work even when she knows the student has a different strategy in mind. I completely felt that same thing in 5th grade as well!

They did not disappoint in their journals! I am wondering if, in us walking around and asking them to verbalize their thinking, it helped them have a clearer picture of what they did? Just a hunch. We also asked them to “show your thinking” instead of “show your work” because we think that has something to do with the direct modeling at times too.

Here was the direct model…

FullSizeRender 34

We had some interesting counting backs. Some counted back dots, like the die. When doing this some put numbers next to the dots while others just used them as dots to count back on. I was so excited to see a student who had counted back on his fingers write out the process. He even wrote the number he started with and ended at the correct number. <- sometimes I see them count that 8 as part of the counting back process and end at 6.

We had a great variety of tools and models, whether used for direct modeling (like the ten frame and tallies) or used for counting back on the number line. The bottom papers were partners so it was interesting to see them do a jump of +3 versus -3. Just as class was wrapping up they were talking about where their answers were because the partner who subtracted 3, said it looked like her partner’s answer was 8 because he added three and landed at 8. Interesting convo to have later too! Their journals also made us realize that we didn’t use the word difference in a way that students knew the answer was called the difference and not sum (yeah, they know sum though:)! Something for us to think more about next time!

Then we saw some great related facts, like this one. I am assuming the number line above also was thinking this but put it on the number line instead of writing the fact. That is another interesting convo to have in future classes!

FullSizeRender 29

This student used a known fact to get the answer and could not have explained it more clearly. I asked her to explain to me what she did and she said, “I knew 8-4=4, if I take one away from the 4 it makes it a 3 and the answer changed to 5.” Wow. Conjectures and claims here we come!

IMG_1192

What a great day! From here, the students do “Start With/Get To” cards as their Ten Minute math that will help emerge subtraction as distance as well as reinforce the relationship between addition and subtraction. They will also play Five in a Row which will allow ideas such as 7-5=6-4 emerge when looking at expressions with the same difference. Of course, many context problems follow from here too so it is going to be so fun to watch what they do with this work!

~Kristin

 

1st Grade Story Problems

18 Replies

Tomorrow I go into a 1st grade classroom to teach a lesson on addition and subtraction story problems. This Investigations lesson for the day centers on students solving these 6 problems, however I am looking to change it up a bit.

While reading my CGI book, Children’s Mathematics, to learn more about the trajectory in which students solve these types of problems, I found this diagram really helpful and interesting….

IMG_1136.JPG

I went into this planning thinking I was going to be looking for how students combined numbers in the context of the diagram above. From there, I was planning to have students do a structured share of their strategies, comparing and contrasting along the way. However, as I got ideas from Jamie (@JamieDunc3) on Twitter, I started to think how much more I would learn about their thinking in talking about their noticings, wonderings, and number choices. My goal has now changed to looking at not only their strategies for combining but how they choose numbers in which they will have to combine.

So…I took the second question, removed the actual question and made it a notice/wonder:

IMG_1132.JPG

Assuming the wonder of how many students were on the bus arose, I would see how students combined the numbers. Would they look for friendly combinations? Would they count all? Model it? Count on? or any combination of those?

Then, I thought I could keep the 13 and leave the other two numbers blank to see what numbers they chose.

IMG_1133.JPG

Did they pick a combination that was easy to add to 13, like 5 and 5? or would they keep adding onto the 13? how would they add with the 13, would they choose 7 to make 20 and then another 1 digit number? would they choose all 2-digit numbers to challenge themselves?

But then, I thought what could happen if I took all three numbers out?

FullSizeRender 22.jpg

For some reason, without the numbers it seems more “wordy” to me. I don’t know why that is? So THEN, I went to this last option….

Screen Shot 2015-11-19 at 5.48.42 PM.png

I really love this one, although, I must admit, I feel a bit out of control of the course of the lesson in choosing this one over the others. But, I think that is what makes it such a beautiful choice. After taking noticings and wonderings, I am thinking of having the students work in pairs to create their own story and solution for one of the wonderings.

In creating their stories, I am concerned that students will choose numbers such as 0 at two stops and 1 at the third and I won’t be able to get a picture of how they combine numbers, however I will have a possible picture of their number comfort level. If they do this and finish quickly, I will be ready with the second choice above to see how they deal with now having the 13 in the problem.

In their journals I will ask them to tell me why they chose the numbers they did for the problem.

I am still thinking about this, so please feel free to leave suggestions and comments! Thanks to Simon, Fran, Graham, and Bryan for their thoughts on Twitter, always appreciated!

~Kristin

 

 

 

 

3rd Grade Subtraction Number Talk

11 Replies

So, this year is tough….getting to know students and content across all grade levels is so exciting but always leaves me with so many questions! As much as I use the CCSS as a guide, I go in to every class wondering what students at this grade know, wondering how they talk about it, and wondering how to structure activities to encourage connections. These are all things I took for granted as a 5th grade teacher.

Today I went in and did a subtraction number talk with a 3rd grade teacher. I did a string starting with the problem: 23 – 19 and all of the other problems were subtracting a number with a 9 in the ones place. I thought I could possibly get adding up, removal and/or compensation strategies. For this problem and the following two, I got at least 3 or 4 different answers and a lot of strategies, some correct others not. The most common was subtracting tens (20-10 = 10) and then incorrectly subtracting ones (9-3=6) and arriving at 16 as their answer. Correct or not, I absolutely loved their openness to sharing and looking for errors in their thinking, it was fantastic! Their thinking was definitely not anything I could even begin to really string together because they were really all over the place so all I can focus on now is where to go from here?

The only common thread I saw was the majority of the students were “number pulling and operating” without seeming to think about the numbers first, what was happening or reasonableness. So, my question now is, Is there a type of number talk that would take the focus off of the numbers for a bit and allow students to think about what relationship the pictures have? I don’t know if this makes much sense but I am playing around with these images, but struggling with the wording…

IMG_0657 IMG_0658

If I flashed the first one, How many did you see? How did you see them?

Flash the second one, What changed? What is the difference? <—–(I like this one suggested by the awesome 3rd grade teacher) Can you write an equation to represent the change?

I am thinking we could get 20 – 5 = 15 or 15 + 5 = 20.

Next this..same questions.

IMG_0659 IMG_0660

Now on this one, 30 – 11 = 19, I think I may bring up the strategy they used today, 30 – 10 = 20 and 1-0 = 1, leaving us with the answer of 21 and see what they think? I can’t tell if that would be helpful or not?? Would love thoughts.

Also, I cannot decide whether to end with a number expression and ask them what the first image looked like and what is different in the second and what the equation would be? Still thinking on this one too.

Trying it out tomorrow and will keep you posted, however I couldn’t sign off without one piece of student work that I loved. I left them today with 36 – 19 in two ways if they could. This student originally got 23 (by the means I described above) but then did the number line and arrived at 17. He went back to the first and realized that 20 and -3 gave him 17, not 23. IMG_0661

When I asked him how he knew it was 17, he said it was like having something 20 feet above the ground and it goes down 3 feet. It has 17 above ground still. I asked him to try and capture that and this is the beautiful piece of work I got…

IMG_0662

Looking forward to seeing this bunch tomorrow!

-Kristin

The Meaning of Subtraction

3 Replies

After a Number Talk a couple of days ago, I blogged about my students’ thoughts around a subtraction problem. Instead of being a talk about subtraction strategies, as I anticipated, it ended up more of a talk about the meanings of subtraction.

After class, I was curious where these meanings of subtraction arise in our curriculum and found this in the 3rd grade Investigations’ Teacher Notes:

gr3Now being in 5th grade, I began asking myself a bunch of questions…If these subtraction meanings arise in 3rd grade, do we ever have students explicitly investigate them? Once they have an efficient strategy to subtract, do we just move on? Do we think that the meanings of subtraction really do not matter if they can read a context and solve for the solution?

After reflecting on my own practice, I honestly think it is a combination of all of these things. I am completely guilty of being satisfied if students are able to understand how to solve a problem, with or without a context, and explain their reasoning. I actually feel quite great about student understandings in that moment, however, I have really seen the importance of having students make deeper connections, create conjectures and justify claims/generalizations. It truly pushes them to think about a deeper meaning of operations and demonstrates the depth of their understanding in developing proof of their thinking.

The day after the Number Talk, I had the class split into two groups and each focused on writing a context that would lend itself to being solved using one of the two strategies for 400-274.

IMG_0508_2After about 5 minutes, I had each group share their context and they did just what I was hoping. The group with the top strategy had a few contexts that all involved having something and then giving something away or losing something. The bottom strategy had a context involving having $400 and leaving the store with $126 and asked to find how much they spent. The second was much more difficult because they kept arguing (in a great way) that it was an adding up problem, not subtraction.

I had each group read their context aloud twice. The first time I could tell everyone was listening to see if it could be solved using subtraction so for the second time, I gave them a listening focus. I asked them to listen for how the two contexts were different, was something different happening in each? After reading them aloud once more, I had them journal what they thought, were they the same type of subtraction problem or different? (They referred to the problems by the student’s name whose strategy it matched).

I loved this student’s wording of the difference as “things happen”

IMG_0529_2

IMG_0524_2IMG_0528_2

IMG_0530_2There was an overwhelming “what is left” and “what the middle piece is” theme among all of the responses as the main difference between the two contexts. Knowing that removal is their primary way in which to think about subtraction, we chatted more about this missing piece and they agreed that they think about that context more as adding up, which makes complete sense to me. It was so nice to hear them talking about the way a context can influence how you use subtraction or addition and how it really was doing the same thing.

A lone student also brought out the constant difference meaning of subtraction during the Number Talk, however he was losing the class in his explanation that day. I didn’t want to lose this idea, so while the others worked on the contexts, I asked him if he minded elaborating more on his idea and creating a visual proof for the class to better explain his reasoning. I got this…

IMG_0521_2He did such a great job of showing two different representations, but I was secretly hoping for a number line with a “shift” in the numbers to really show constant difference. He instead showed removal with same difference. I adore the top piece and just as I was thinking of how we could make that more visual for the class today, Simon (of course) responded with a brilliant visual…

At the beginning of class today, I asked the student who wrote the response above, what he thought about this visual and he said, “Well, that is just like what I was saying.” I asked him if he could work on a claim for the way he is thinking about subtraction while I asked the rest of the class to see if they could think of a claim that this representation would support. This was such an interesting reversal of the usual process I use with student claims, but I was excited to try it out!

I got many ideas in terms of the bars such as these…

IMG_0550IMG_0552I then showed them Simon’s second idea…

…and asked them to think of these more as subtraction problems and see what they could come up with in terms of noticings and/or generalizations. I got some awesome responses! IMG_0550 - Version 2

IMG_0548Then we shared the original student’s claim he worked on to see if it matched their thinking…

IMG_0553I love that he was not only thinking about what was happening in the problem, but also why he would want to use this in order to make a problem easier to solve.

These lessons were a beautiful way to work forward and backward in making claims. Thank you Simon for being so amazing, as always, it was not only great learning, but great fun!

My students never fail to leave me with something to think about. One student said he thought of “partial differences” and here is how he explained it (definitely not what I thought when he said the term)

IMG_0547My next task is thinking of questions to ask him about this….

-Kristin

Subtraction Number Talk: My Curiosity Today…

6 Replies

Subtraction is the one operation that every time it arises in class, throws one more thing for me to think about into the mix. I have two recent posts around decimal subtraction, here and here, and I continue to work with whole number subtraction through number talks.

Today, I only had time for two problems in the Number Talk due to testing 😦 The first problem was 400 – 349. I was most anticipating students would subtract 50 and add one back or add up from the 349 to the 400 (1+50) to arrive at the answer of 51.  I was surprised when a student said he “subtracted 100 – 49 to get 51 and knew that would be the same answer because if you added 300 to both numbers it would give you the same problem, so the same answer.” This made me think of a distance model on a number line, but I completely missed that opportunity and moved into the next problem. Seeing what happened next, it may have either made one strategy more clear or completely caused us to miss out on the conversation that followed.

Problem #2: 400 – 274

IMG_0502_2The student, “M”, on the right subtracted to find the distance between 400 and 274, however did not explain it that way so it left many students wondering how she knew what to subtract. I had a student ask her if that was her second strategy because she seems to have subtracted the answer from the 400.

The student, “C”, on the left solved it the way the majority of the class did, removal in part with some compensation at the end. Before he started explaining, he prefaced with, “I did it pretty much like M.” When he finished, he realized it was not the same and was confused as to where “M” came out with the same answer. He even exclaimed that, ‘I think she got the answer by mistake.”

“M” knew exactly what she did, however, I didn’t let her explain yet because I wanted the rest of the class to think about it a bit more. I told her she would be able to explain it tomorrow after we chat a bit more with it. I had them all end the class with a journal entry (surprising, right?:) I asked them what they understood, saw happening in each, or were not too sure about. It is just the most beautiful thing to read the honesty and reflection in their writings.

Some students could see what was happening…(even though it seems some tables have the vocabulary a little mixed up:)

IMG_0509_2IMG_0506_3Some left confused…

IMG_0504_3IMG_0508_2

Some had a really interesting way of thinking about it…

IMG_0505_3And then there was “M” who cannot wait to share tomorrow…

IMG_0503_2

Now, the question is, how to approach this tomorrow? I am thinking I would love three groups, one who subtracted in parts, one who found the distance by subtracting back to the minuend, and one group who adjusted the subtrahend and minuend to find the distance between. Have them create a context and representation that shows what they did (still working within the same problem they all have the same answer for) and do a share. I would like the share to go in the exact order of the groups I just listed above. Crossing my fingers I have time to talk some more math with them tomorrow, a silent classroom is probably more torture for me than them 🙂

-Kristin

Subtraction Is So Conceptual

3 Replies

Every year, across all grade levels, I hear (and observe) subtraction being a difficult concept for students. Not just a difficult calculation, but concept. I am not talking about reading a context and knowing if subtraction could be a way to solve it, but instead, what is happening when you subtract and how does a change in the subtrahend and minuend impact the difference? I think students can learn a procedure to “operate” with subtraction (as with any operation), but I always question the conceptual understanding behind their work. I also think that we, as teachers, sometimes make some assumptions about student understanding of subtraction when all of their answers are coming out correctly. It feels really nice to see students read a task and solve it correctly with subtraction, but have they thought about whether the answer makes sense or could they explain what would happen to the answer if I increased or decreased one of the numbers in the problem? This could completely be my own wondering because, I admit,  I tend to question a lot of my students’ understandings until I hear them talking about the idea or working through it in their journals. To get a better understanding of their thinking and attempt to help them move forward in their thinking, I do Number Talks a lot and most recently have really started to listen and think more about what makes subtraction so difficult for them.

I have a few ideas based on my observations of the students’ conversations and many lie in the fact that we do much relational thinking about addition and subtraction that students assume that the numbers operate in the same manner.

1- Commutativity. When adding, it is so convenient that you could add the tens and ones in either order and still end with the same answer. For example, when adding 34 + 63 I could add (30+60)+(3+4) and still result in the same answer. Even if it changed the context of the problem, it would still result in the correct answer. Whereas, with subtraction if I was subtracting 63-34, I can’t just do (60-30) + (4-3). It now creates a different problem but it is something that students do ALL of the time in order to take a smaller number from a larger one. Which is what I see happening here with the quick subtraction problem I gave students to solve last week before we started looking deeper into decimal subtraction.I just wanted to get a look at what they were thinking, as was not surprised to see this on many papers.

IMG_9644_2IMG_9642_2

2 – Number Adjustments and the Effect on the Context. This comes out A LOT in our talks. When they are adding, they love to compensate and adjust the addends to make an easier problem. For example, 49 + 33, students would take one from the 33 to give to the 49 to make an easier problem of 50 + 32. Again, it would change the context of the problem they were solving, however not impact the result. Now given 49 – 33, giving 1 to the 49 from the 33 leaves you with 50 – 32 and completely changes the context. Given a removal problem, you are starting with more, but taking away less. Or given a distance problem, you have moved the starting and ending point in opposite directions. There is SO much context in a subtraction problem in just the number adjustments themselves.

3 – Number Adjustments and the Effect on the Outcome. When adding, students understand how adjusting one of the addends affects the solution. If I add one more to this addend it increases the sum by one or if I decrease both addends by 1, the sum will decrease by 2. Again, the context can come into play here, but the students get pretty comfortable with the numbers, stripped of context, in understanding this. Now, subtraction is not so nice in that way. Again, context is SO important. 34 – 12 = 22. If I take one from the 34, making the problem 33 – 12 = 21, it works in the way the students know addition works. However, taking 1 from the 12, making the problem 34 – 11 = 23, it does not. They are so perplexed when they try this and it instead adds to the original difference.

Now, because students do not feel as comfortable with subtraction, I also see less willingness to reach outside of the standard algorithm once they “get it to work”. I appreciate the use of the algorithm, however after this quick formative, I had the feeling that there was some conceptual understanding missing that would really impact our decimal work. Because of this, I decided to start with an Investigations story problem on our grid paper.

“Mercedes had 1.86 grams of gold. She used 0.73 gram of it in a piece of jewelry. How much gold does she have left?

I asked them what this story would look like on grids and I got quite a variety of thoughts but I was very surprised to see students putting all three numbers (the two in the problem and the difference) on three separate grids.

IMG_9665 IMG_9666

I did have a quick realization of the difference between “Show this problem on the grids” and “Show how this story looks on the grids?”

These showed the STORY….

This student taped the removed part over top of what she had, to leave the answer in purple:

IMG_9669IMG_9670

This student set the whole aside because she knew she didn’t need to touch it and dealt with the hundredths.

IMG_9668

These involved some taking away of pieces to leave them with the answer.

IMG_9663IMG_9662IMG_9664

This student changed the whole to be the tenth, but represented each number in the equation.

IMG_9667To see if they made a connection between what they had done on their grids to the solution process, I asked them to solve it in their journal the way they would have just given the problem (again, most with the algorithm) and then tell if it was similar to what they did on their grids. Many struggled to see any similarities which surprised me, especially with the way some took away the tenths and hundredths on the grids.

IMG_9658IMG_9661

IMG_9656_2IMG_9671

This was so interesting to me especially when I saw so many correct answers in their journals but when asked to explain, it was tough! Subtraction is tough…for students and adults. Not the calculation so much, but the concept of what is happening. It is so conceptual and really hard to break away from methods we know that work for us to truly understand the meaning behind them! I know I still have to think harder about subtraction then I do addition, so I want to make it clearer for my students.

So much to think about and I am sure I have so much to learn about subtraction and connecting representations to their thinking, but this is a stepping stone along the way!

-Kristin