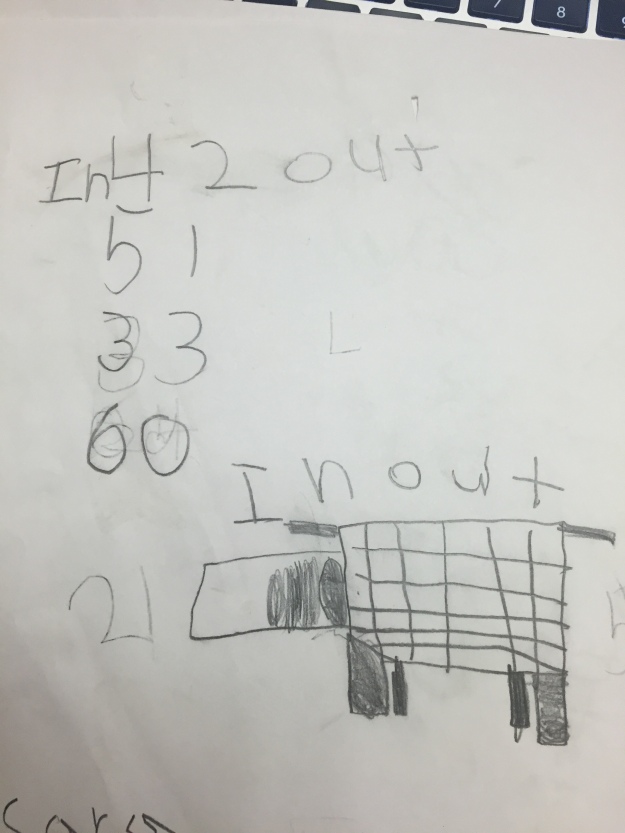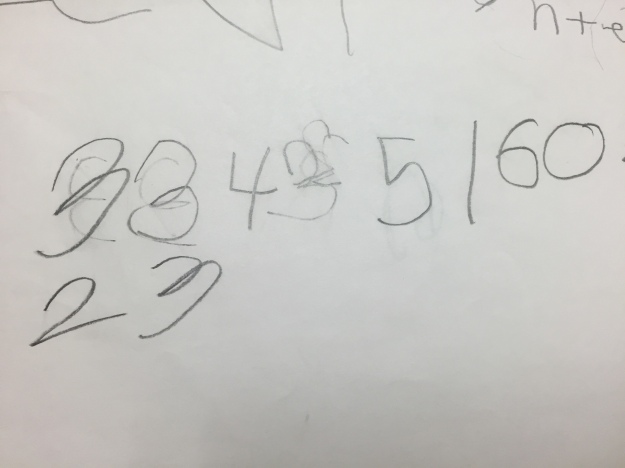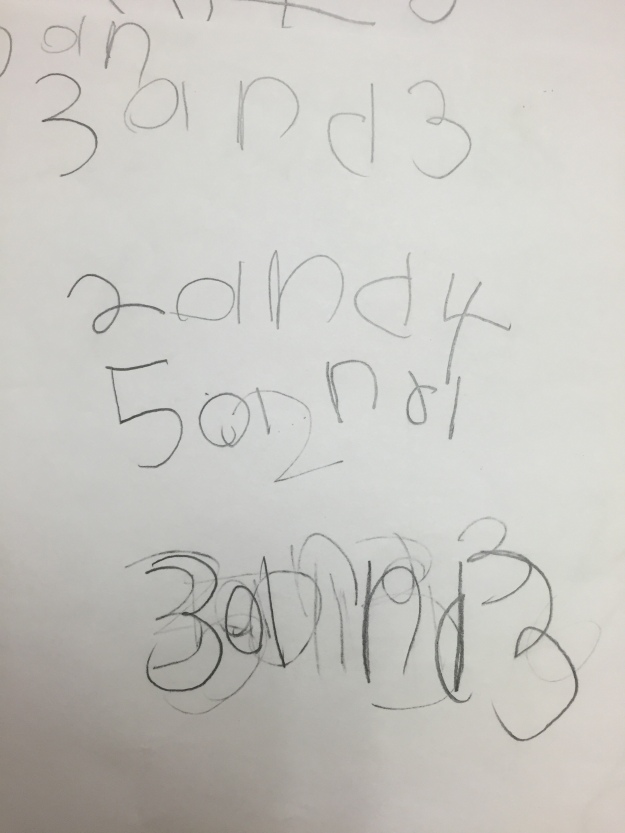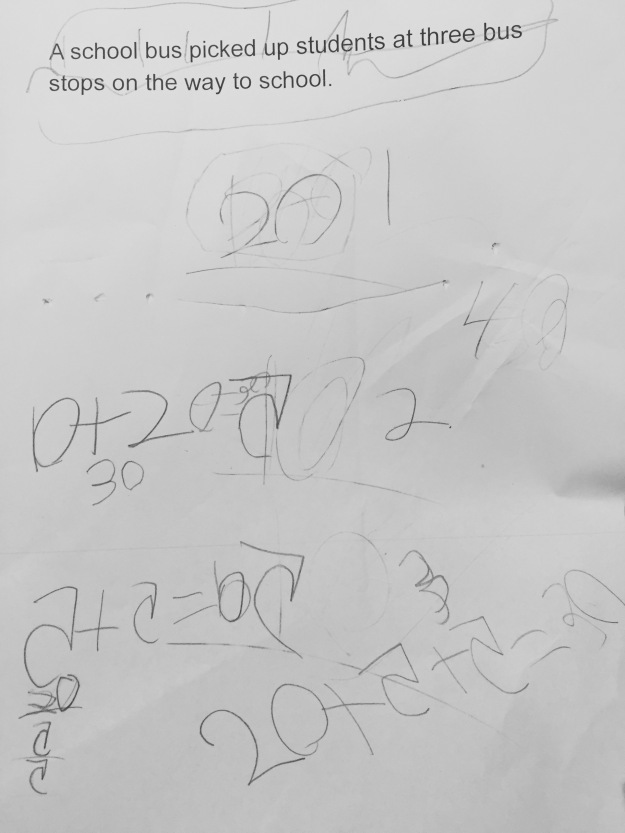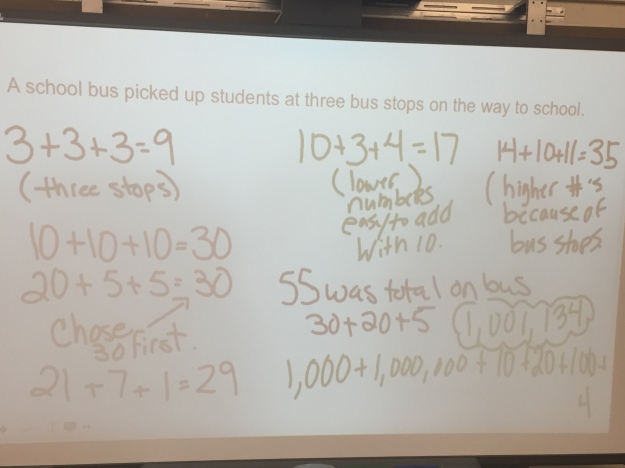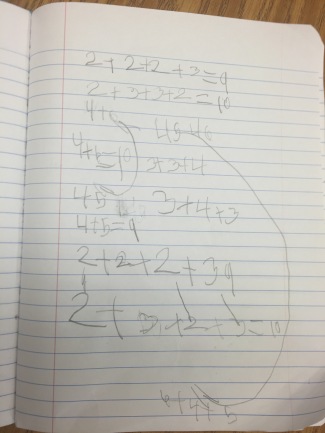Yesterday, I had the chance to teach the 1st grade lesson I planned here. It was so much fun and SUCH a learning experience for me! After all of the conversation in the comments and on Twitter, I decided to start with the open, one sentence Notice/Wonder. Only having 45 minutes and this being the students first time doing a N/W, I decided not to begin with a number talk/routine (which I usually always do).

The students started on the carpet, I put up the sentence, read it and asked, “What do you notice and wonder about this sentence?” Just then a student exclaims that he just noticed that “Notice” was not, “Not Ice.” At that moment, I began thinking maybe my question had them looking at the physical pieces of the sentence/words so I quickly rephrased, “I would love to hear what you notice and wonder about what is happening in the sentence.” They used their Number Talk signals, thumbs up when they had a notice or wonder and then used their fingers to indicate more than one. I was so impressed by all of their thoughts, but I did realize that is it hard to end their wonderings! The amazing thing was how all of their wonderings really could turn this sentence into a story in their ELA class because they were all really important details they could add to it. Here was how the board ended.

I asked which wonder we could work on together today in class and there was a unanimous vote for “How many kids are on the bus?” however there were a few that suggested, “How many student can the bus hold?” because “math is counting things and we could count the seats.” I starred the wonder “How many kids are on the bus?” and told them next time they get on their bus I would love to hear how many seats and students they found are there. We discussed whether they know how many students were on the bus by reading our sentence and they said no, they only know that there were 3 stops. I asked, what they would want to know and they wanted to know how many kids were at the stops. I wrote that at the top.
When I told them they would get to choose how many students were at each stop, they were so excited! I gave them a paper with the sentence at the top, let them choose a partner and sent them on their way.
As I walked around and asked students why they chose the numbers they did, I quickly wondered how much I should have helped organize their work for them. I found so many with numbers everywhere and it was hard to see where their bus stop numbers were, let alone their total. Should I have put Bus Stop 1____, Bus Stop 2____, and Bus Stop 3_______ to have a clearer picture while also modeling for students how we can make our math work more clear? Quite a few looked like this…
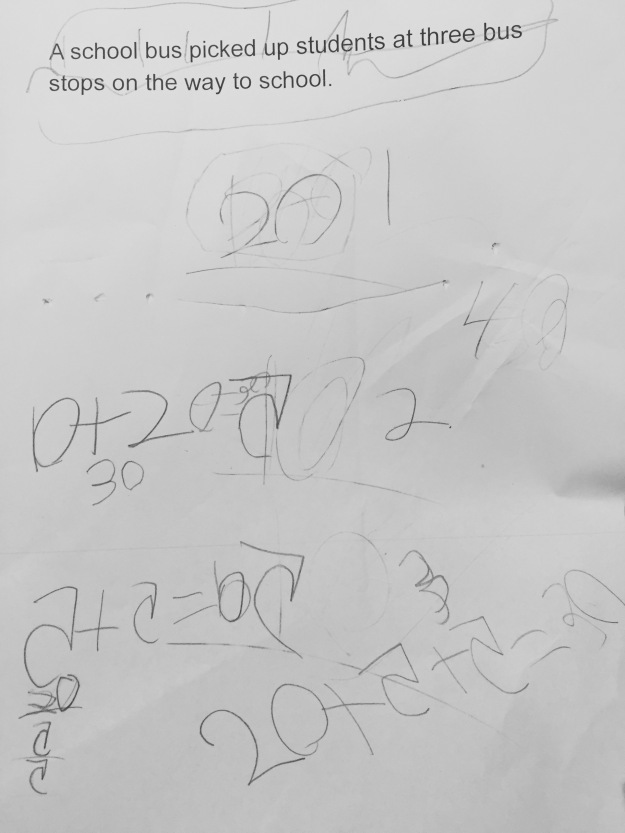
There were so many interesting papers, so I love WordPress’ new tiling feature for pictures to make it look less cumbersome!
Top Row, Pic 1: This student had 24 as two stops. When I asked him how many stops we noticed in the beginning, I got a “Oh gosh” and he wrote Bus stop 1, 2, and3. He then stuck with the 24 and when I came back he had 8, 8, and 8. I didn’t see this until after class so I am curious how he arrived at that answer. I also realized that these 1st graders move fast and it is SO easy to miss the cool things they do so quickly!!
Top Row, Pic 2: They said 3 and 22 were easy to add and then they just chose another small number. The interesting thing here that I need to find out more about is the 5×6 with the one box shaded in. I loved the commutativity showing up here!
Top Row, Pic 3: This was so interesting because I had never thought that a student would first think of how many students were on the bus and divide it up from there. They thought 30 students would fit on a bus so they made the stops fit that information. (They saw the error on the last one during the share).
Bottom Row, Pic 1: This student said that because there were 3 stops, there were 3 students at each one and ended with 9.
Bottom Row, Pic 2 &3: This student wanted big numbers so his first response, after he insisted on re-writing the sentence, was 1,000 and 1,000,000 and 4. Then on the back of his paper he wanted 6 stops and chose 6 new numbers. This led to some great conversation during the share.
This student figured that if there were 1 or 2 at a seat then there would be 55 students on the bus. I love all of this work so much! Then when I asked her about the students at each stop, she said, 30, 20 and 5.

We shared as a group back on the carpet and I tried to capture why they chose the numbers they did:
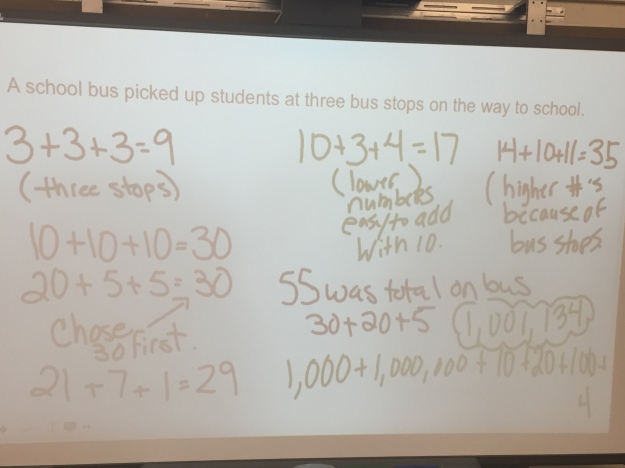
I then gave them the original problem and asked them to solve it individually. After seeing them work on this problem, I think there are so many interesting conversations that could happen Monday morning!
This is where I had so many questions as to how we get the younger students to make their thinking more visible. I found so much of it happens on fingers, 100s chart, and number line on their desk that I was getting an equation on the paper. It is great when I am sitting there asking, but that cannot obviously happen when they are done so quickly and there a bunch of them! Is this something that comes with practice? I did find that once I asked them if they could explain to me on the paper how they solved it, they did a great job. My next question is, would taking the 100s charts and number lines off the desks help push students to look for friendlier numbers? I found the majority of them went left to right, counting on instead of using the 6 and 4 first. This is something that I think a structured share out on Monday could bring to light for those who never thought of it.
Here are a sampling of the papers I look forward to chatting with the teacher, Lisa, about on Monday. We can chat about how we can structure this share out.
Lisa, through number talks and investigations, has been working a lot on having students noticing number patterns leading to generalizations. It was neat to see this work of adjusting addends and keeping the same sum showing up here too. It seemed to show up most after they had their answer and were playing around with the numbers, which I love!!
I am happy to have started with the open notice/wonder because I learned so much about how they think about problems and I think the opportunity to choose their own numbers got them thinking about the context over solving for an answer to an addition problem. I am, however, extremely curious how it would have changed the work if I had given students the problem with the 13 given and the other two missing? Would I have seen more about how they choose numbers to make the 13 easier to add a third number? I am hoping to get into another 1st grade classroom to try this out with another teacher but I would love it if any other 1st grade teachers would there would love to try it out and report back!!
I am so looking forward to Jamie’s post on this because her student work looked amazing on Twitter yesterday!!
~Kristin
Yeah, Jamie’s post is up! Check it out here! Cannot wait for our Google Hang Out tomorrow to chat all about it!