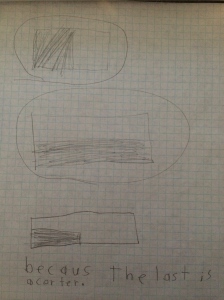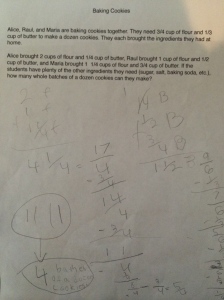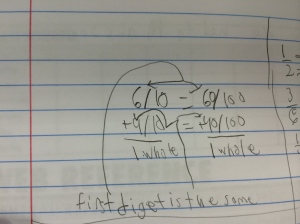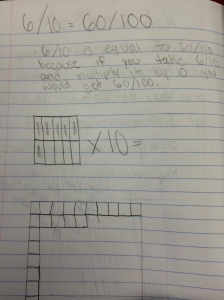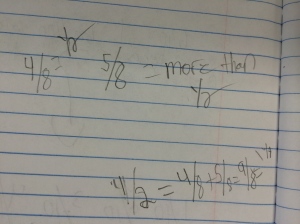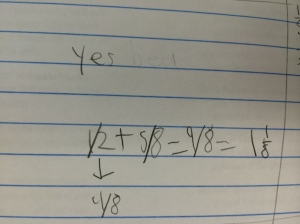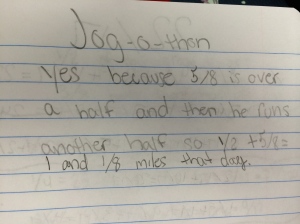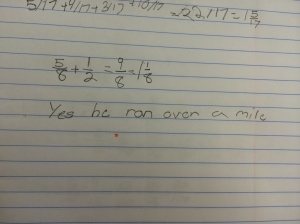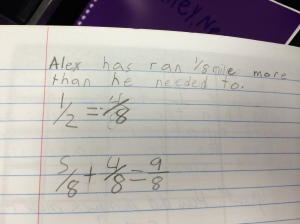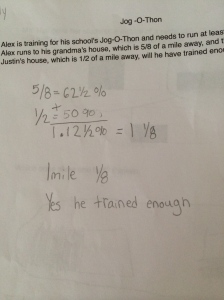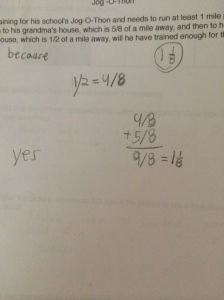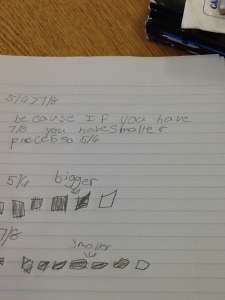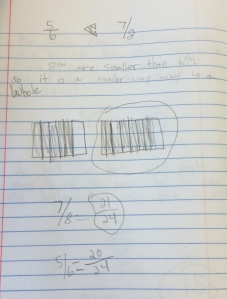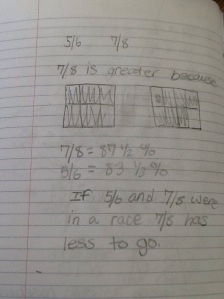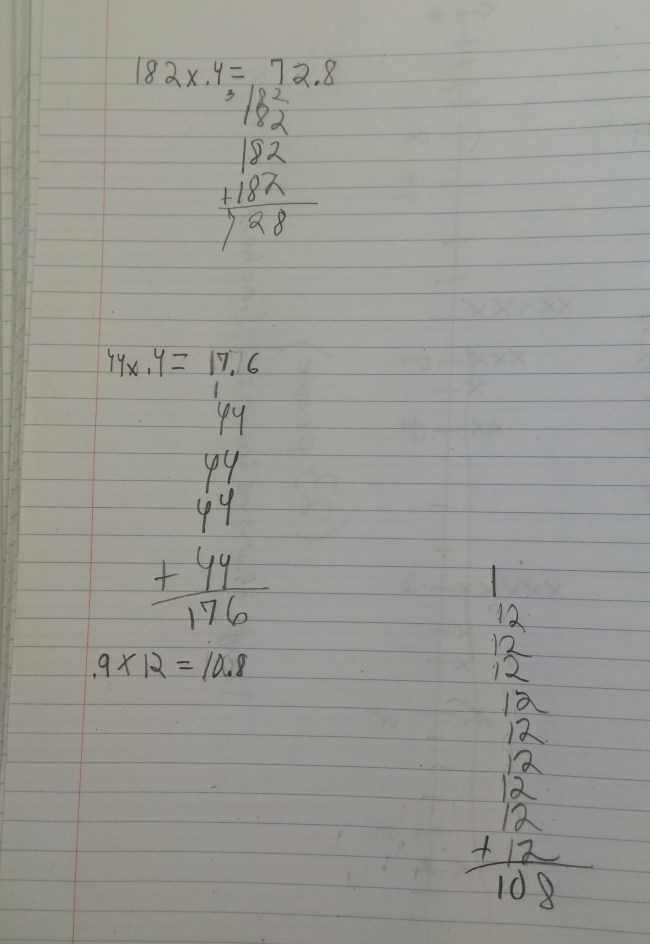At the end of August, I was fortunate to be selected to participate in a project through Illustrative Math, Smarter Balanced, and the Teaching Channel focusing on the fraction learning progression of students in grades 3 – 5. We are working on creating,piloting, and revising both instructional and assessment tasks that will live on the both the Illustrative and SB digital libraries. Video of this work in action will also be captured by, and live on, the Teaching Channel website. Our team is a unique mix of educators from coast to coast. Jody (IM Project Lead & Orange County Math Supervisor), Chepina (Math methods professor from KSU), Alicia (5th grade teacher from Washington state), Jennie (Alicia’s math coach) and me…5th grade teacher on the opposite side of the country! Aside from this immediate group, we have many others at both Illustrative and SB offering guidance and feedback along our way.
The first phase of this work was using a multiplication of fraction task as the center of a professional development for Orange County educators as well as the filmed lesson for the Teaching Channel. Due to the distance between us, Google immediately became our best friend! We shared documents and created our presentation in the Drive, shared thoughts and ideas through Gmail, and had many Google Hang Outs to collaborate and meet each other virtually! It was so exciting to be working together on something we all feel so passionate about…student learning around mathematics. We worked through the task together, thought about the 5 Practices in planning the lesson and designed a type of lesson study around our work.
After the PD planning was almost complete, I did the instructional task with my students, filmed the lesson, and uploaded it to Teaching Channel Teams (if you haven’t checked this resource out, I think it is an amazing opportunity for groups to collaborate around video). All of the team members viewed the lesson, made comments, and offered suggestions to improve the lesson when Alicia teaches it in the upcoming week. As an aside, the channel allows for time stamping on the video comments so you can jump right to the point of the comment, great stuff. We planned the afternoon of our PD day around this task and used work samples and video of my students to help build deeper teacher understandings around how students reason about fractions.
Planning complete, and I am off to Orange County after my half day last Friday! After a long 6 hour flight and a nearly missed connection, I arrived at the John Wayne Airport 3 hours earlier than the time my body was saying it was! That evening I got to “meet” Jody and Chepina for the first time….but not really! Google had made it feel like I already knew them! I met up with Alicia and Jennie the following day and we had such an amazing PD day. Who doesn’t love teachers who come to a professional development on a Saturday?!? We had such an interesting group of college professors, CGI reps, public and charter school teachers, and a Smarter Balanced representative. We looked at coherence of the standards along the grade levels, read the fraction progression document, did some math as learners, and reflected on that same math as educators. The math conversations were amazing and the personal ah-has in terms of fraction work, happened at every turn! I even met a new math tweep (@edtechbydarin – 5th grade math teacher) and coerced Jody to hop back on to check out Twitter (@jody_guarino)! Follow them both, they are great!
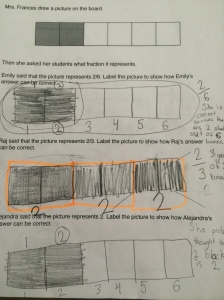
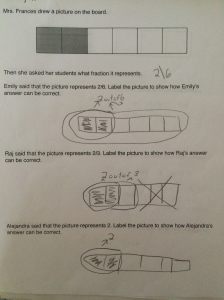
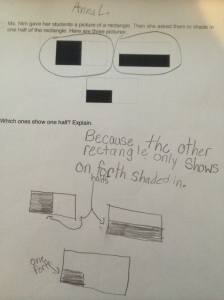
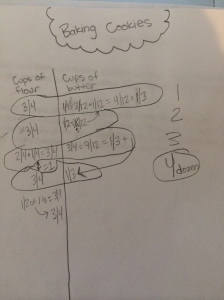
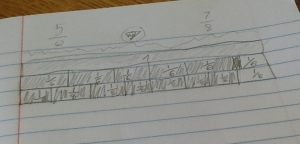
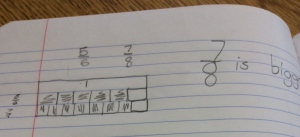
Next week, I will be heading out to Seattle to see Alicia teach the same lesson I taught and that we revised together. Jennie will be in the room coaching during the lesson and then we all film for the Teaching Channel on our collaboration and reflections on student work. I cannot wait to see how Alicia’s students do with the new and improved lesson. We changed up the number talk and adjusted the wording of the task. I will post pics and update with the task and some sample student work soon! Here is just a glimpse at some of my student work that guided our conversations about the lesson…
Next steps are going to be writing some formative and summative tasks within fractions! Exciting stuff, so glad to be a part of it!
-Kristin
PS – This $15 for internet on the plane has been the BEST thing ever! I may blog so much more if I am traveling to the west coast!