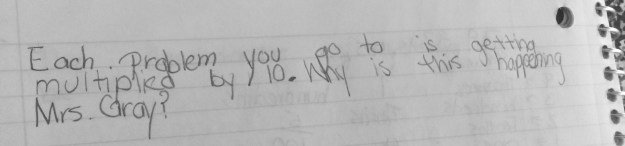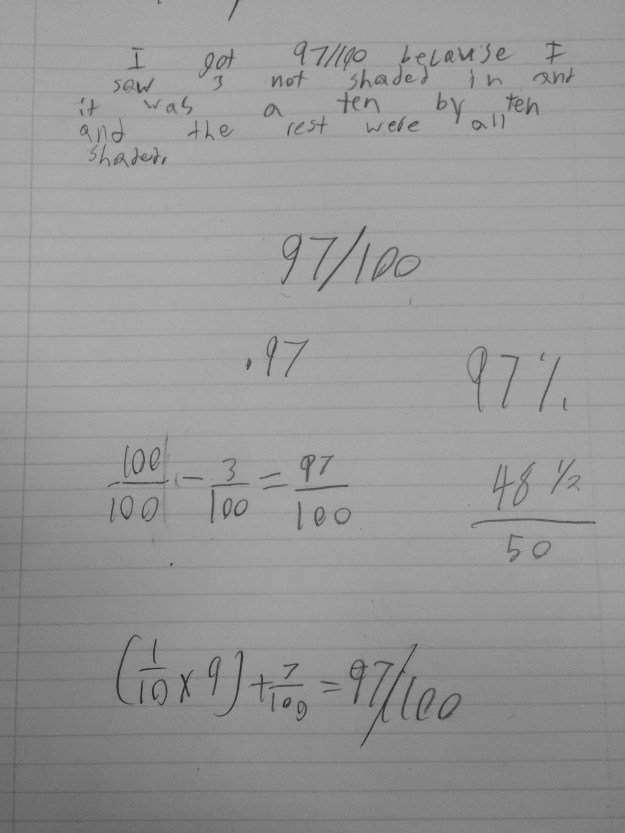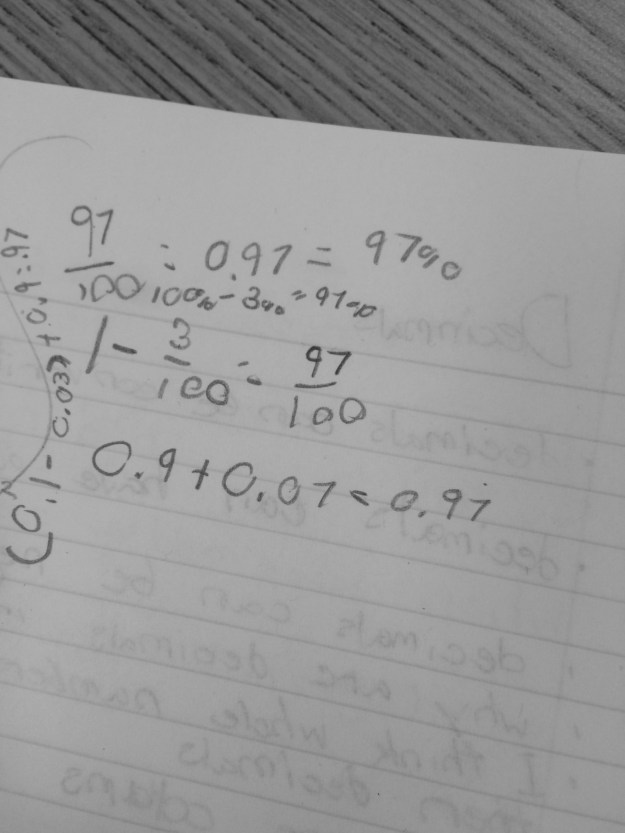Understanding student thinking is so hard. I make assumptions. I read into things. I SO want to believe there is understanding behind everything they write on their papers. However, it is so much more difficult than that and my most recent difficulty is addition of decimals.
We have talked about decimals in one frames, shaded grids, and I am confident that every student can compare decimals with understanding of place value and magnitude. They understand decimals independently. Then, enter decimal addition. What is it about computation that sends students right back to not thinking about the numbers themselves and straight back to “lining them up” and adding? I know it is not that they CAN’T think about the numbers, so then my wheels start turning…. is it just ease of use? Great. But is it ease of use with understanding? Or is it ease of use without understanding but just gets them the right answer? This is where teaching is so hard!
We do number talks at least 2-3 times per week and given a problem such as 38 + 47, the majority of the students would say 40 + 45 = 85 using a compensation strategy. Today, given 6.8 + 4.7, I got “I lined them up and added 8 and 7 and got 15, carried the one…” You can hear the rest. Wait, what? Where are the tenths? Where is the place value? Why didn’t I ask them to give me an estimate first (ugh, hindsight)? I ask for any other strategies, nothing emerges. I am left to wonder what they truly understand about addition of decimals. Is it the decimal place value that takes away from thinking about the numbers or is it simply that they see how the decimals operate like whole numbers in a base ten sense. After doing a contextual task the day before, with pencil and paper, I was excited by the outcome, there were numerous strategies. However, if pushed to solve mentally, the students reverted back to an algorithmic feel. I am not saying that it means the students do not understand the place values they are adding, but trying to bring to light how hard it is to interpret their understanding on my part.
I then gave them a problem involving three decimals and asked them to solve it two ways. I was trying to get a better feel of their understanding. The two ways would push those “liner-uppers” to work with the decimals in a different way and also allow me the time to walk around and question students about their work. I was not shocked to see that the majority went to lining them up as their first strategy, however I was very excited by their second strategy that showed more understanding of place value.
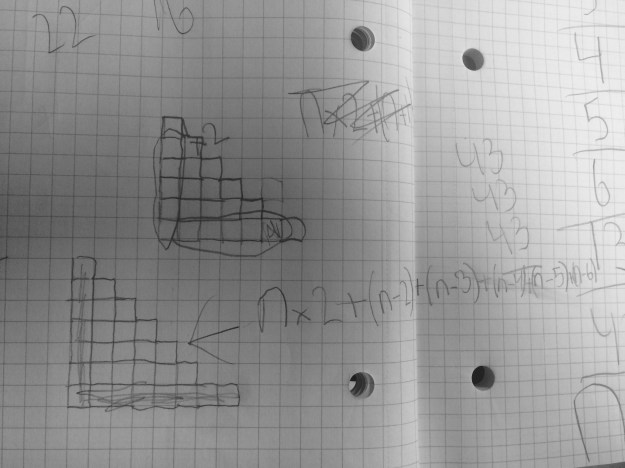
Here are some examples of the students solving 0.98 + 0.05 + 1.06
I loved the number line in the first example and the breaking apart of the 0.05 in the second example. I was starting to see the flexibility and thinking that I want to see in my students.
I gave my second class a different problem involving two decimals, both in the hundredths that were not as “friendly” as the decimals in the previous example. I was happy to see the variety of strategies, including my student who starts assigning letters for each digit. He said he is ready to start doing some algebra 🙂 I love it!

 I had a few who finished fairly quickly, so I gave them the problem 0.8 + 0.75 + 0.625, and then they started getting creative! This is one answer that was so interesting and will be the way I kick off my class tomorrow. His reference to columns and boxes are the hundredths grids we used for the Fill Two game.
I had a few who finished fairly quickly, so I gave them the problem 0.8 + 0.75 + 0.625, and then they started getting creative! This is one answer that was so interesting and will be the way I kick off my class tomorrow. His reference to columns and boxes are the hundredths grids we used for the Fill Two game.
 Today was a day that really showed me how hard it is to understand student thinking and how important it is to push students to explain their understanding in more than one way. I could have very easily assumed that every student could add decimals by place value because they lined them up and added to get a correct answer. However, if not given the opportunity to show another way to think about the problem, how would I truly know? I still have a few students who are getting the correct answer but are not able to articulate their process, so I am going to do a lot more estimating to get them thinking about the numbers before the operation. Going to be a fun day in math tomorrow!
Today was a day that really showed me how hard it is to understand student thinking and how important it is to push students to explain their understanding in more than one way. I could have very easily assumed that every student could add decimals by place value because they lined them up and added to get a correct answer. However, if not given the opportunity to show another way to think about the problem, how would I truly know? I still have a few students who are getting the correct answer but are not able to articulate their process, so I am going to do a lot more estimating to get them thinking about the numbers before the operation. Going to be a fun day in math tomorrow!
-Kristin

























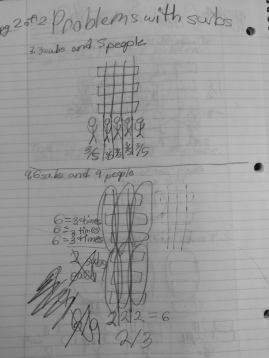

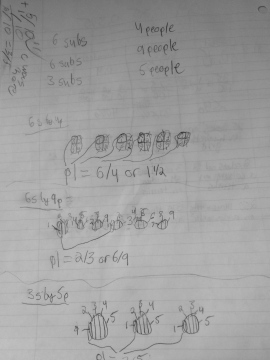


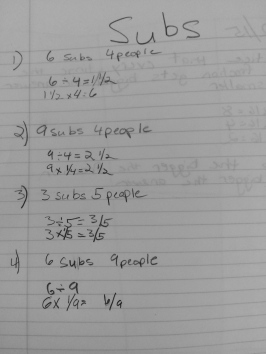
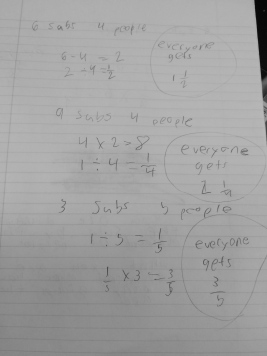
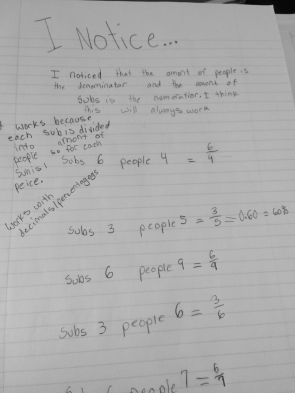
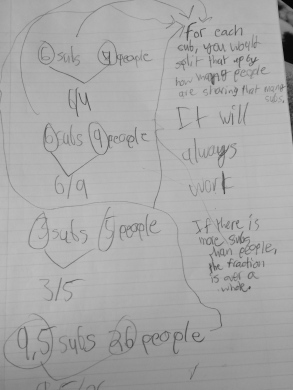
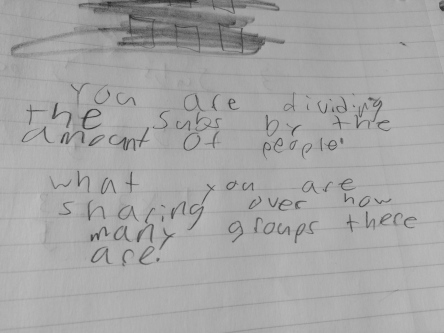
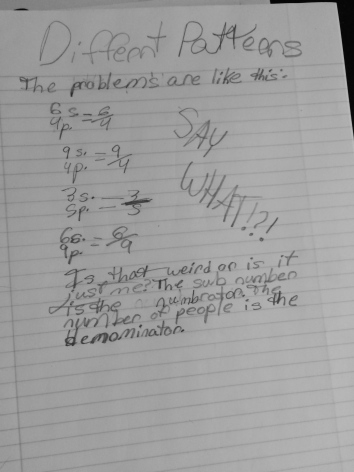


















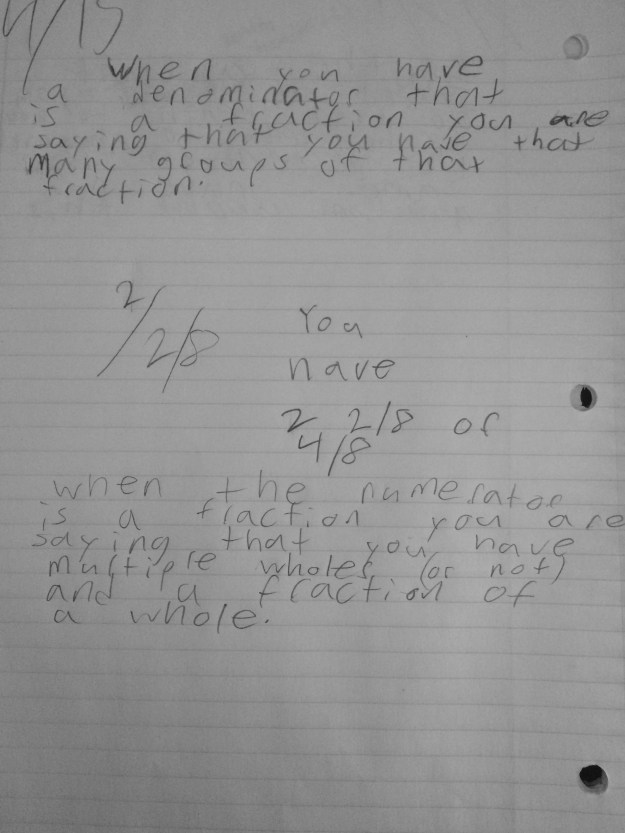


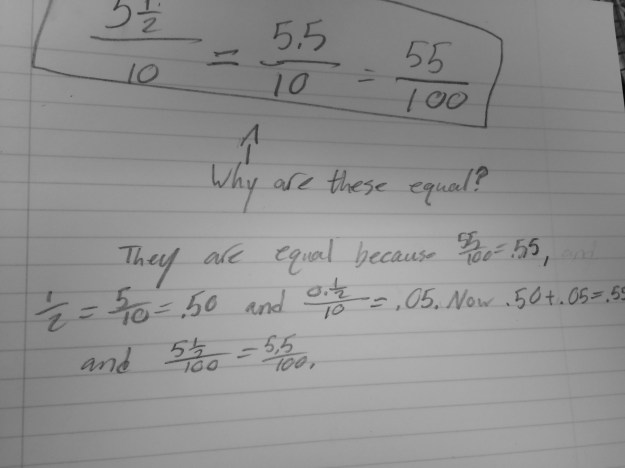
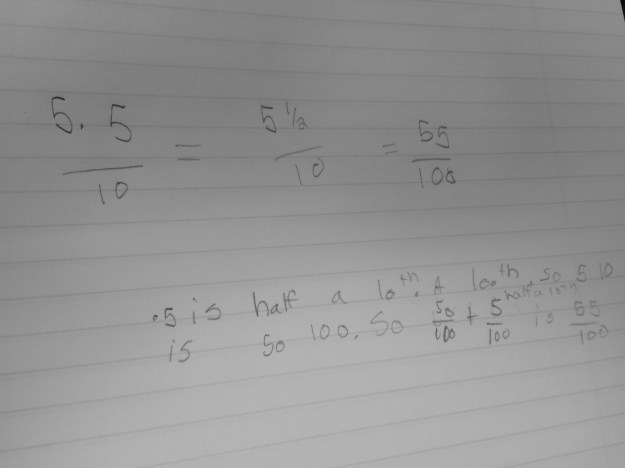



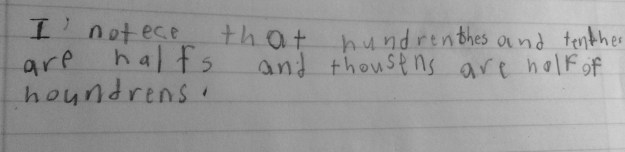

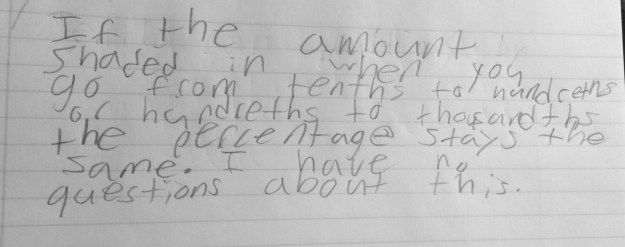
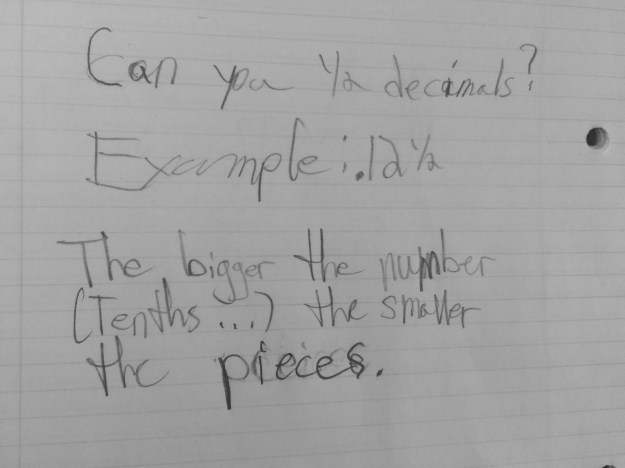

 To use the word differentiation here is an understatement. The range of thoughts in my classroom (and many many others) amaze me on a daily basis, in the most wonderful way!
To use the word differentiation here is an understatement. The range of thoughts in my classroom (and many many others) amaze me on a daily basis, in the most wonderful way!