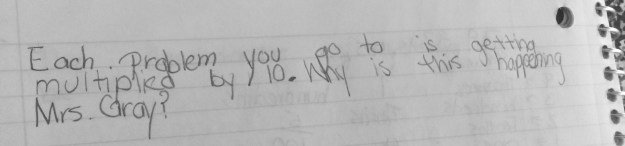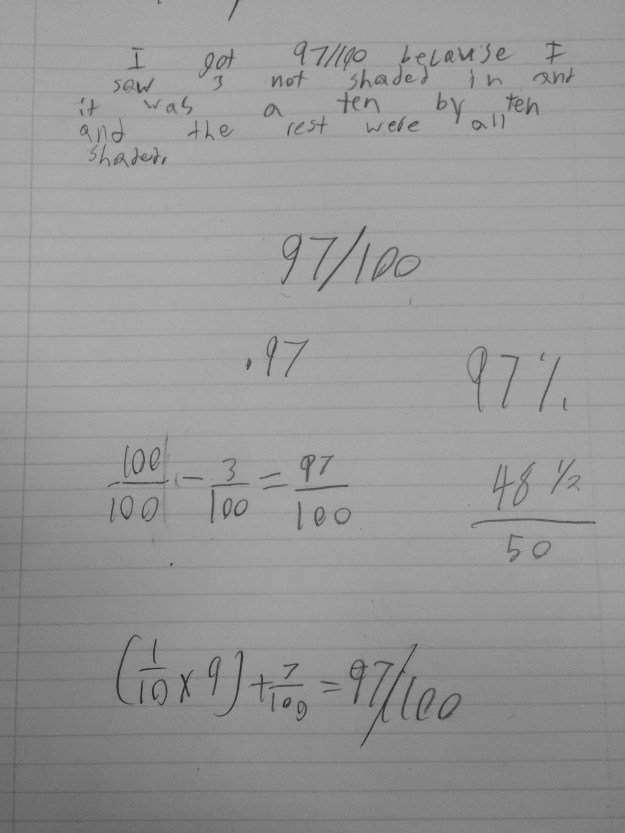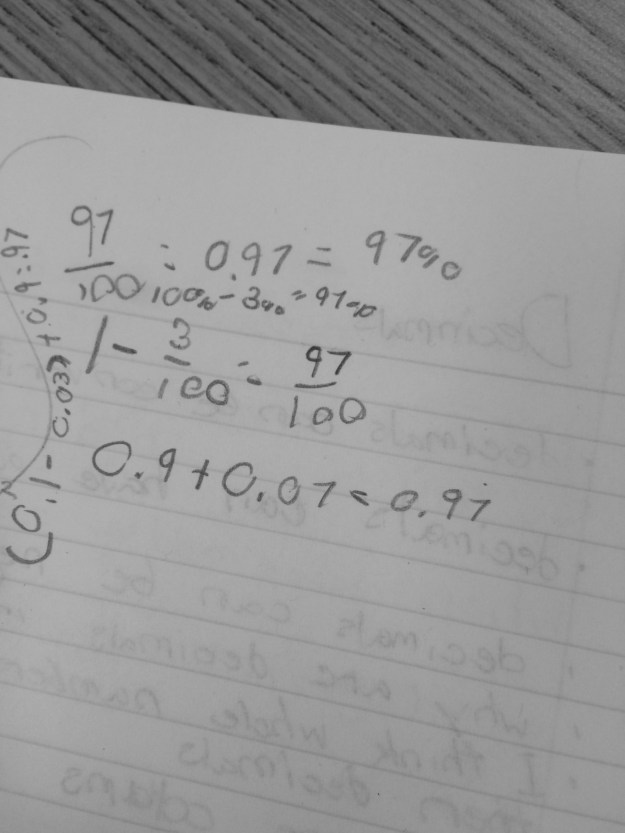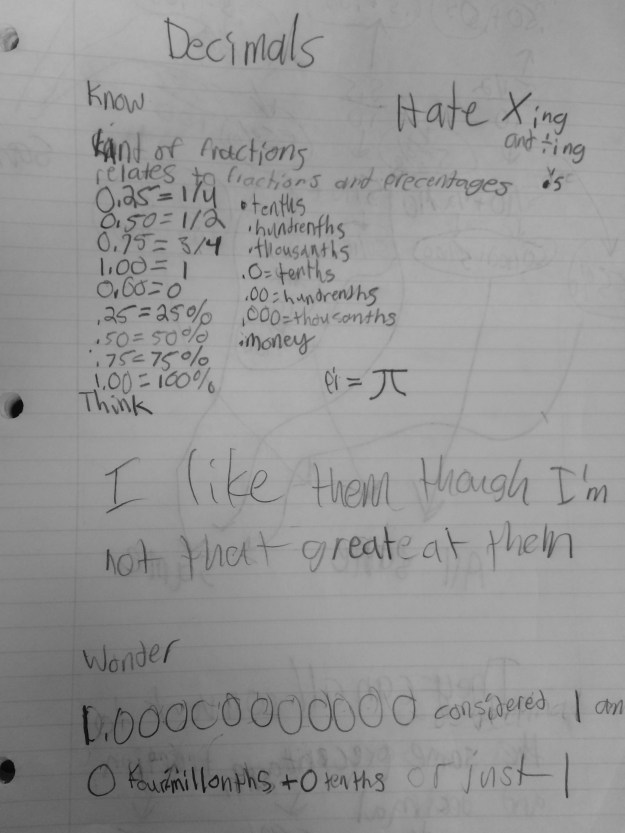I love reading and giving feedback on my students’ journals, I make time for it every day. But the mere thought of grading papers (feedback or not) makes me world’s biggest procrastinator. Unfortunately, my reality is that I need grades for progress reports and report cards, so I make the best of it. I try to make the assignments valuable for both the students and myself in their learning, however I always wonder why I don’t approach the papers the same, they are both student work right?
I had a realization yesterday while I was grading, as to why I make time to read their journals vs the aversion I have to grading papers. While I was grading, my mind was focused on what the students DON’T know, what they aren’t getting, aggravation at the careless mistakes, aggravation that I didn’t “reach” that child and why they don’t all have 100%. As I graded, I was busy making notes in my own journal of the students who were missing certain items so I could make my plan for next week to help them better understand the material. And while I know this is invaluable in planning to better teach my students, I realized I was completely glancing over what they DO know. I was checking off the problems they were getting correct and focusing solely on the wrong. Don’t be mistaken, I LOVE mistakes in math, I love analyzing what students could have been thinking, misconceptions and/or misunderstandings, but when grading, the feeling is still not the same.
This focus on “wrong” wasn’t the only thing that bothered me though. I also wasn’t “feeling” my students’ voices in the assignments, like I do their journals. Maybe it is because I love hearing them talk about math so much, their journals are the next best thing when they have left class for the day. Maybe it is the freedom for them to take more chances in their journals or simply say, “I don’t understand it from this point on..” that makes them so much more enjoyable. Or maybe it is the mere fact I don’t have to put a grade to their thinking. As I read their journals, I am looking at everything they DO know and how that led them to where they are instead of the other way around.
Their journals feel more like the way we learn then grades do. We try, we make mistakes, people help us along the way with advice, we try again, we test things out, we look back at what we did to build on it….no number is attached to that, so why grades? I would like to think I try my best to not have grades be a focus in my classroom and instead be a snapshot of where students are right now in their learning, but those assignments still do not hold the same value that their journals do for me.
Maybe someday standards based grading will make its way into our district but until then I will continue to read their journals for things just like this…







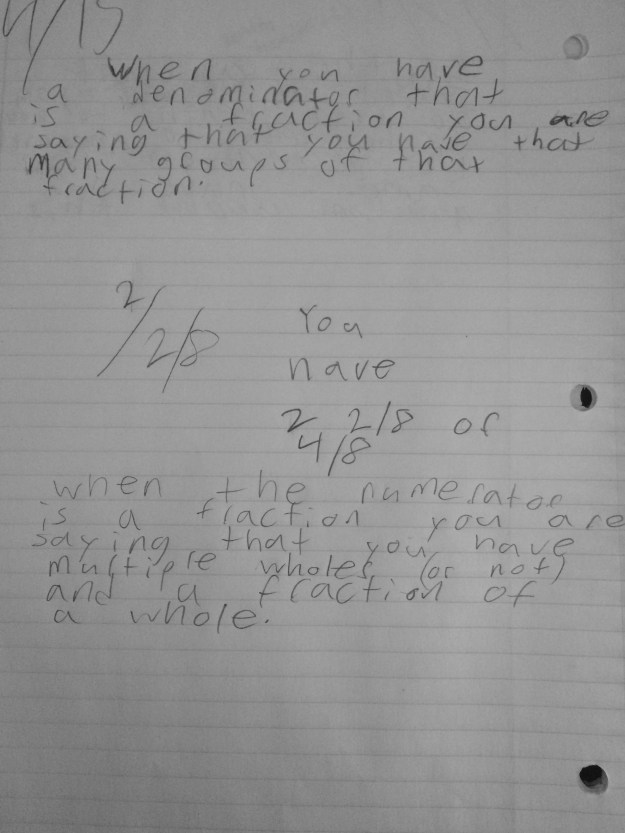


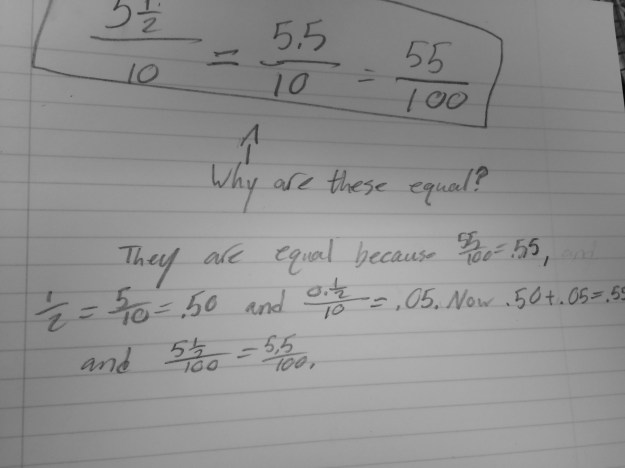
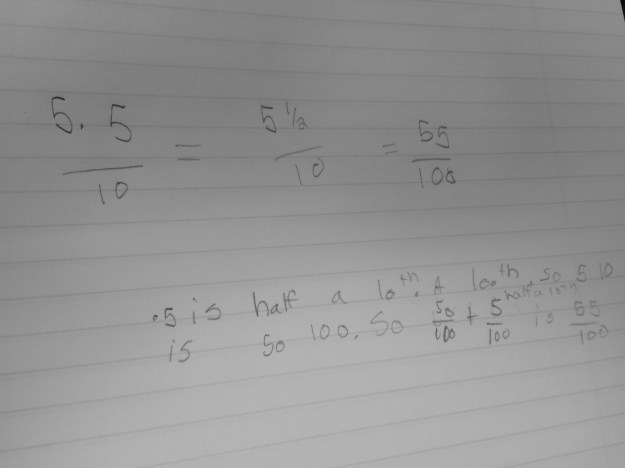



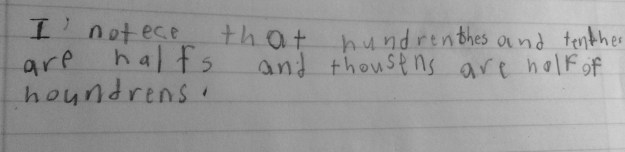

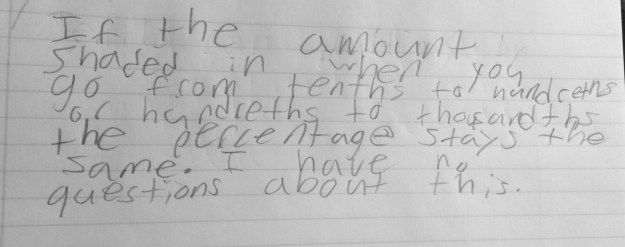
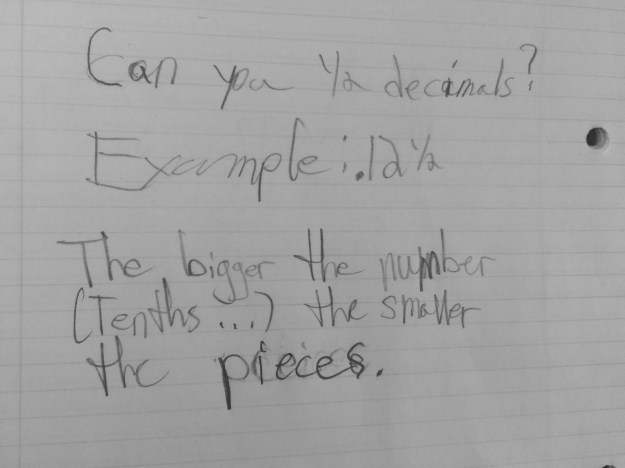

 To use the word differentiation here is an understatement. The range of thoughts in my classroom (and many many others) amaze me on a daily basis, in the most wonderful way!
To use the word differentiation here is an understatement. The range of thoughts in my classroom (and many many others) amaze me on a daily basis, in the most wonderful way!