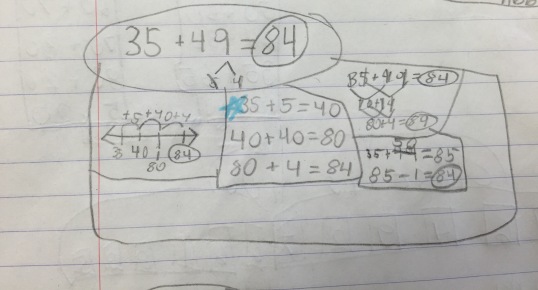
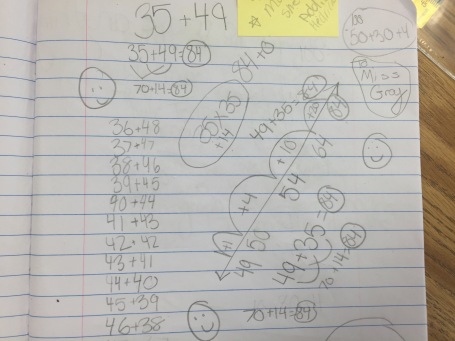
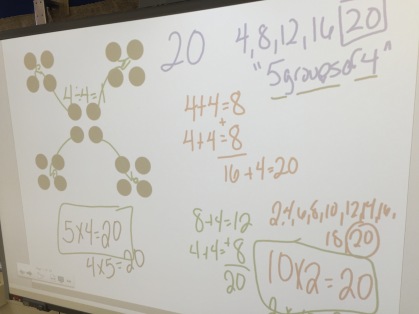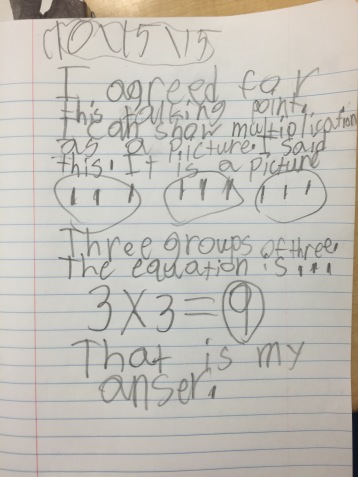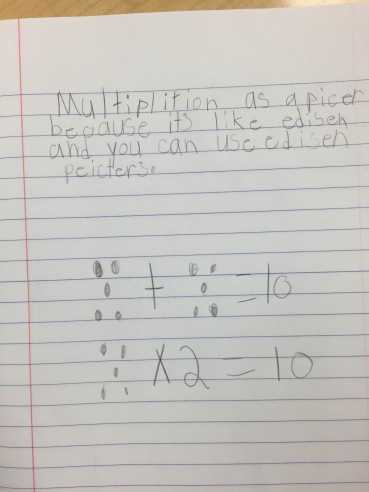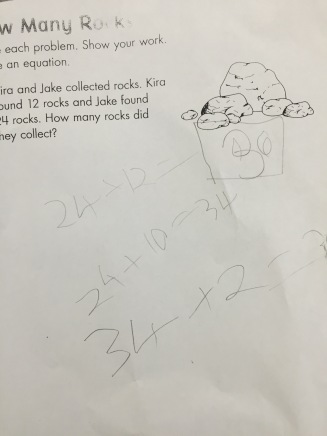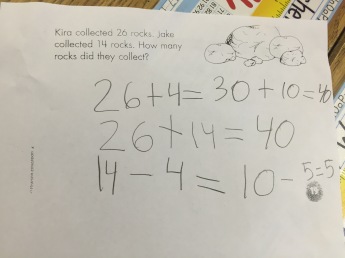1st Grade Dot Addition

3 Replies

Tomorrow I get to teach with a 1st grade teacher, Lisa! I am super excited! To give a bit of background, the students up to this point have done a lot of dot image number talks. These talks have been a mix of just dots with no particular order and others with subitizable dots. The main focus has been becoming aware of how students are organizing and/or combining the dots. Are they counting all? Counting on? Using known facts? Or using any combination of the three strategies? In their Investigations work, they have been building on these talks using the 100’s chart and number lines to represent the addition and subtraction contexts.

Today in class the students will be learning how to play Dot Addition, so we will be building on that work tomorrow when I join them.

We decided to build on this work and launch the lesson with a string of three dice images. Just to make it a bit interesting, we set the dice equal to each other and ask them how we could prove if it was true or false.

Image 1 – Hear if students recognize that order of the dice doesn’t matter in finding the sum

Image 2 – See if students decompose to form equivalent expressions

Image 3 – See how they talk about decomposition with three addends versus two. Can they be equal with more on one side?

Next we will review the game and show the change in game boards. Instead of finding sums of 6, 8, 10, 12 to 6, 9, 10, 15. Now, here is where I am wondering about what the changes are in student thinking? There is SO much in here! Is it about combining strategies? Is it recording? Is it how they decompose? Is it compensation? Is it the relationships between the addends and sums that students need to start to look at? Holy cow, we had all of these conversations in our planning and we are still not sure we have it right, but here is our plan from here:

Observe them play on the new game board and take note of how students are find the sums.
Pull out strategic expressions that we want to highlight in the group share.
Ask students what they would do if they didn’t have a card they needed. For example, what would happen if there was no 5 and you needed it? What could you do? or Could you have made that expression with more than two cards? How do you know?

After they play, we have two options. If there are a variety of expressions, we will bring them to the carpet to look at a completed game board from my game with Ms. Williams that contains the expressions they have arrived at also. If there is not a variety, we will complete a blank sheet together, gathering all of the expressions they did have and then ask them to turn and talk to see if they could come up with different ways to write these equations with the cards.

If we use our completed sheet, it will look like this:

We were going to ask them to take a few minutes to look at the expressions within each sum and then talk about what they notice. For example, within 6 do they notice that you can either “move a dot” or decompose and the sum stays the same?

If that goes smoothly and we make it this far without running out of time, we will ask them to do the same noticing between different sums. Do they notice that you add three to every expression in 6 to get to 9? Do they notice that somewhere in the 10 expressions there is an extra 1 from the expressions in 9? Do they notice the 5 when moving from a sum of 10 to a sum of 15?

So much to see! I cannot wait! Would love any thoughts and I will be posting the follow up soon!!

-Kristin

Kindergarten Number Lines

7 Replies

Today I had a great day of planning with a kindergarten and 1st grade teacher for lessons we are teaching together on Thursday and WOW, has it been such a learning experience for me! The best part is, we have a whole day to get feedback from anyone who would like to offer it before we try this all out!

In Kindergarten, the students have been counting collections, counting dot images in various ways and since I have been obsessed with the clothesline lately, we thought this could be the perfect mash-up! When I read the counting and cardinality learning progressions, however, I did not see anything in there about number lines in Kindergarten but I did find this in the measurement progression:

“Even when students seem to understand length in such activities, they may not conserve length. That is, they may believe that if one of two sticks of equal lengths is vertical, it is then longer than the other, horizontal, stick. Or, they may believe that a string, when bent or curved, is now shorter (due to its endpoints being closer to each other). Both informal and structured experiences, including demonstrations and discussions, can clarify how length is maintained, or conserved, in such situations. For example, teachers and students might rotate shapes to see its sides in different orientations. As with number, learning and using language such as “It looks longer, but it really isn’t longer” is helpful. Students who have these competencies can engage in experiences that lay the groundwork for later learning. Many can begin to learn to compare the lengths of two objects using a third object, order lengths, and connect number to length. For example, informal experiences such as making a road “10 blocks long” help students build a foundation for measuring length in the elementary grades.”

In thinking about this, I tweeted out about number lines in Kindergarten and immediately was reminded by Tracy of her post on this work from last spring! Awesome stuff! I sent the link on to Nicole, the teacher I am planning with, and we were both filled with so many ideas! We were both thinking about relative location on the number line but hadn’t thought more specifically about the equal distances between each number! We also were originally going to do the number line as a whole group, but after reading Tracy’s post we changed our plan to allow for more discovery and exploration of the number line!

Here is the plan….

Students will be in groups of 4. Each group will have a strip of tape on the floor in different areas around the room.
We decided to put the tape the length of 5 tiles to see if any group uses the tiles in thinking about space.
We will hand each group the same card one by one and ask them to decide, as a group, where it should be placed. We went back and forth with this one…we wondered whether we should just let them start placing, but we really were so curious to see their moves and adjustments with each card. We also thought that since they have been ordering numbers lately, the majority would just put each card next to one another on the line.
Now, the order of the cards…this was so much fun to talk about….
- 1 – to see if they place it at the beginning and then the adjustment when 0 comes up.
- 10 – to see if students put it at the end of the line and how they determine the distance from 1
- 0 – to see if students place it to the left of 1 and if they have to move the 1.
- 3 – to see if students but it closer to 1 than 10, how close to 3 they place it, and if they put it less than half.
- 9 – to see if students think about 1 less than 10.
- 5 – THIS IS THE CARD I CANNOT WAIT TO SEE! Since they have been doing ten frames so much, some students are comfortable with 5 and 5 is 10, so do they apply that logic here?
- 7 – to see if students put it right in the middle of 5 and 9.
- 6 – one less than 7 or one more than 5.
- 2 – between 1 and 3.
- 4 – again, one more or one less
- 8 – same
During all of the placing time, we will be listening and recording any important ideas we want to have students talk about when we go to the whole group discussion.

After each group has placed the cards, we will have them do a gallery walk to the other groups’ lines and ask them to talk about what is the same, what is different at each line. We will then gather on the carpet.

We have a clothesline up, much longer than their strips of tape to do the same cards as a whole group. We will give each pair of students one card to talk to each other where they would put it (based on their work in the earlier group work). *Something we did not think of until I just typed this was how we partner the students up…we should match them with a student from a different number line to vary the convo.

We will call the cards up in the same oder they did their group work and ask the pair to explain where they decided to put their card and why. After all the cards are placed, we will ask them what was important to them as we made our number lines and record that for future conversations.

As a future conversation, we thought it would be really cool to see what connections the students make between the number line, ten frame, and dot images they have been working with so much!

Also, if anyone knows of a children’s book that has something moving a distance of 10 or 20 units, I would love to hear about it! Every single book I read dealt with 10 as collections of things, never distance.

-Kristin

Too late to type up the 1st grade one now, but it will be around this Dot Addition game in Investigations: http://www.smusd.org/cms/lib3/CA01000805/Centricity/Domain/198/Dot%20Addition.pdf Will type that one up tomorrow!!

How Planning Mistakes Can Lead To Great Student Thinking….

4 Replies

The other day I did this fraction clothesline activity with a 5th grade class and today I had the chance to do it again with another 5th grade teacher, Leigh. It is always so nice to get to have a do-over after having time to reflect and think more about what the students thought about both during and after the activity.

I really thought the conversation was great during the clothesline activity, but it took too long the first time. We noticed that some students began to disengage. To try and improve upon that, Leigh and I decided to give only one card to every pair of students instead of each student having one. However, due to us wanting to keep a few important cards we wanted to hear them talk about, some pairs had two.

I also did not like my placement of 0 being at the very end of the left (when looking at it) end of the string. I moved it out some and talked about the set of numbers that falls on either side of the 0. I felt much better about that this time around!

In the planning of the first clothesline activity, we took fractions from the work the students had been doing with percents and decided on putting 100% in there, completely thinking it would be at 4/4. As the student placed it, however, I started realizing that I never thought about the difference of 100% in terms of the area representations the students had been using versus 100% when talking about distance on a number line. But now, having time to reflect on the card, I thought it would make a great journal entry!

As we neared the end of the card placements, I handed the 100% card to a student and told her it was going to probably cause a lot of discussion but just put it where she thought it went. She said she got it, walked up there and placed it on top of the 2 (the highest number on the line). There were some agree signals going on and some other hands that shot right up to disagree. We talked about it a bit and then we asked them to journal their ending thoughts so we could move on with the rest of the lesson about different sized wholes.

Some thought that 100% was at 4/4 on the number line because it equals 1….

Some thought it was at 4/4, but because of the conversation became a bit unclear…

Some thought it goes on the 2 because it is the biggest number on the number line…

Some related it to different contexts with different wholes…

And one student said it can be anywhere with beautiful adjustments as it moves….

What a great day revisiting my planning mistake!

-Kristin

3rd Grade Dot Image Number Talk

6 Replies

Since the 3rd graders are entering their multiplication unit, I find it the perfect time for some dot images!! I used the image below as a quick image in which I ask them to think about how many dots they saw and how they saw them. Quick images are so great for pushing students to visualize the dots and move beyond counting by ones and twos. I flashed the image for about 3 seconds, gave students time to think, and then gave them one more quick look at the image to check and/or revise their thinking.

They all saw 20, however the way they the 20 varied a lot and the conversation was amazing from there! Here is how our board ended up…

Recording is something that I am always working on, making truly representative of the students’ thinking. The first thinking was adding groups of four to get 16 and then the additional middle 4 to arrive at 20. The second was skip counting, so I asked the student to do that for me and how they knew to stop at 20. He said he knew it was 5 groups of 4 so he needed to stop after 5 fours. Then I wrote under that “5 groups of 4.” From there a student jumped on that and said that was the same as 5 x 4, because they were talking about that the day before in class.

Then, the thing I was hoping happened, happened. A student said she did 4 x 5 because that was easier. I wrote it down and, of course, ask if that is the same thing? We began on open discussion and they agreed it was the same answer but the picture is not the same. I asked how it changes and a student told me to move a dot to the middle of each of the outside fours to make fives. I drew the arrow and then one student said that is like division, 4 ÷ 4 because you are splitting that 4 between the 4 groups. I let that sit for those not ready for that yet.

The last strategy was counting by twos so I had him skip count for me and recorded that. I asked if we had an equation to match that thinking and got 10 x 2. At that point, I was ready for them to do some algebraic reasoning.

So I wrote 5 x 4 = 10 x 2 and asked them if that was true or false. They unanimously agreed yes so I asked them how they could prove that and to write what they noticed and/or wondered about it. Here are their whiteboard work:

This one showed the 5×4=4×5 to me but I loved the notice so much:

This one was an interesting decomposition of the 4 to show where the two tens are coming from in 2 x 10:

This was a beautiful notice and wonder on the groups changing and wondering if this is with every multiplication problem….how AWESOME?!:

This one required a conversation because I couldn’t really understand it. The movement of dots made two groups of five to make the ten they said, but it was more their noticing/wondering that I want to explore more with them:

Oh my goodness, how much do I love this mention of al(l)gebra in here and then the notice about the half of 10 is 5 and 2 is half of 4…this could have some potential conjecture-making in future talks:

This one is incredibly hard to understand and I am not even sure I completely do, but I love how she used one image to “make” the other:

This student started with decomposing the four (I know we need to think about that equal sign later) but then moved to talking about ten frames. He said if I put two ten frames on top of one another (one attached under the other) I can see five fours (vertically). Then he said he drew them side by side and he saw 2 tens. HOLY COW!

What an amazing conversation with this group! Today I posed them with a few of these noticings and wonderings and asked them to pick one and see if it always worked and why. I didn’t have time to snap pics of their journals but all I can say is 3.5 x 10 came up…so I will have to blog that this weekend!

All of this K-5 work is so exciting and it is so amazing to hear and see all of the great teaching and learning going on around the building!

-Kristin

5th Grade Fraction Clothesline

2 Replies

Today, I had the chance to plan and teach with a 5th grade teacher and it was awesome! Last week, this class had just finished a bunch of 100s grid shading in thinking about fraction/percent equivalencies, so we picked up planning the lesson in Investigations with the fraction/percent equivalent strips. Instead of the 10-minute math activity, we thought it would be really interesting to do the clothesline number line to kick off the class period.

We chose fractions (and one percent I will talk about later) based on the fractions the students had been working with on the grids. We chose fractions based on different comparison strategies that could arise such as:

Partitioning sections of the line
Distance to benchmarks
Equivalent Fractions
Common Denominator
Greater than, Less than or equal to a whole or 1/2

We settled upon the following cards:

1/4, 3/4, 4/4, 1/3, 4/3, 5/10, 2/5, 100%, 3/8, 1 5/8, 1 7/8, 4/5, 11/6, 1 6/10, 1/10, 9/8, 12/8, 2

To start, I put the 0 toward the left of the line (when you are looking at it) and we practiced with a few whole numbers. One student volunteered to be first and I handed her a card with the number 7. As she walked up, looked around, walked up and down the line, looked at me like I was playing some type of trick on her, we immediately had the conversation about how knowing the highest numbered card would be super helpful. She settled on putting it toward the far right side and had a seat. I gave another student the 10 card. He put that at the far right and adjusted the 7 to be “about 2 cards away” from the 10, leaving a really long distance from 0-7 for them to think about. We had some students disagree so we talked about distance and adjusted the cards to be more reflective of distance. Since the conversation of half of the distance to 10 came up, I handed another student the 5 card and he placed it right in the middle. The discussion went back to the 7 and they decided that since 7.5 would be halfway between 5 and 10 that 7 had to be a little bit less than the halfway of 5 and 10.

Then, we moved into the fraction cards. We gave each pair of student two cards. In hindsight, for times sake, I would probably only do one card per pair. I gave them one minute to talk about everything they knew about the fractions they had and then we started. I asked for volunteers who thought their card would help us get started and called on a boy with the 1 7/8 card. He went up and stood all of the way to the right and said he couldn’t put his on. I asked why and he said that since the cards were all fractions the line could only go to 1 so his is more than one and can’t go on here. I asked if anyone in the class had a card that may help us out and a student with the 2 card raised her hand. She placed her card all of the way to the right, said “maybe it goes to two” and the other student placed it just to the left of it because, “it is only 1/8 from 2.” Awesome!

We went along with the rest of the cards and so many amazing conversations, agreements and disagreements happened along the way. There are a few things that stand out in my mind as some great reflections on the activity:

A student had placed 5/10 halfway between 0 and 1. The next student placed 2/5 just to the left of the 5/10 because, “I know 2 and a half fifths is a half so that means that 2/5 has to be less than 5/10. It is a half of a fifth away.” The NEXT student volunteered and placed 3/8 overlapping just the edge of the 2/5 card on the left. I was expecting percentages to come out, since that was their most recent work with those fractions, however the student said they knew 3/8 was an 1/8 from a half and 2/5 was a 1/10 from a half and an 1/8 and 1/10 are close but an 1/8 is just a little bit further away. Awesome and definitely not what I expected!
I wish I had not put the zero so far to the left. Looking back I am wondering if that instills misunderstandings when they begin their work with negative numbers on a number line similar to the original misconception that launched the activity with the 1 7/8.
Oh, the 100% card….complete mistake on my part, although it may have been a great mistake to have! In the first class, the student with the 100% card came up and said, “I have 100% and that is 100/100 which is 1” and put it in the appropriate place on the line. Just as she did that, I started thinking how I never really thought about the distinct difference between percent in relation to area (like the grids they had been shading) and 100% when dealing with distance on a number line. No one seemed to notice and since I didn’t know exactly what to ask at that point because I was processing my own thoughts, I waited until another student placed 4/4 on top of it and erased it from my immediate view!
- I stayed for the next class and this time I was prepared for that card and now really looking around to see what students’ reactions were when it was placed. As soon as the student placed it at the 1 location, I heard some side whispers at the tables. I paused and asked what the problem was and they said, “100% is the whole thing.” The next student who volunteered had the 2 card, picked up the 100% card on the way to the right side and put the 2 down and the 100% on top. Lovely and just what I was thinking.

I have never had students reflect on the difference of talking about percentages with distance versus area because I had never thought about it! It definitely feels like an interesting convo to have and a great mistake that I am glad I made!!

I will be back in another 5th grade class tomorrow and will see what happens…it could make for a great journal writing!

-Kristin

Dots, Dots, and More Dots…the Planning Stage

2 Replies

About a month ago, Andrew Stadel sent me the following set of dot images and asked for thoughts:

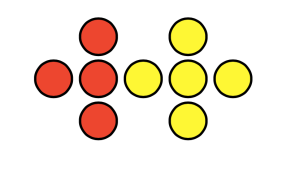
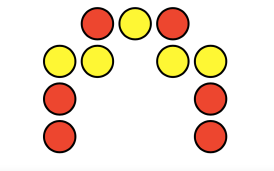
Of course, being accustomed to doing Quick Images through Investigations, my first thoughts were around what this would look like as a sequence of images. I sent him this reply:

“Are you thinking of these being shown one after the other….like image, discuss how many and how you saw it, next image, discuss how many and how you saw it, next image…etc? Or are you thinking of using them as stand alone dot images? I am not even sure if that impacts my thinking around the purpose, but here are my initial thoughts (but I do want to think about this a bit more…) “

Now, while I am used to Quick Images, they do not have these yellow and red counters that the students use a lot in the younger grades. That made my begin to split my thoughts into how I may use them for 3-5 versus K-2. So, my thoughts to Andrew continued like this….

“For my 3rd – 5th I would love to show these in a progression as I could possibly be focusing

on three things:

How they think about the red vs yellow (the two colors, it screams distributive to me).
If they create an array and subtract out missing, visually move the dots to create a “nicer” image, or if they build in parts.
How the recordings connect…I typically ask “Where is ___ in ___?” For example in the second image a student could see 2 x 4 +1=9 while another could see 4 + 5 =9 so where is 4+ 5 in 2 x 4 + 1? Well if we decompose that 5 into 4+1, we have 4+4+1 = 2x 4+1 ….Those conversations are probably my favorite with this stuff!

K-2 I am still really learning a lot about and full disclaimer, in my purposes with them, I typically lean toward making connections to 10 (100 for 2nd) and comparisons. If my purpose was to see how they see the dots, recreating the image, and counting this progression would be perfect…especially that last one!!

However, if my purpose was to have them compare (more or less) and then creating a proof, I

would have the second image to build upon the first….like maybe add a yellow on the top an

bottom of the first image…so the first one they say, “I saw 4 (of course we ask how they saw

that four) then 2 and 2 and 2.” We ask how could we record that? 4 + 2+2+2 = 10. First flash of

the second image, “Is it more or less than the first? How do you know?” Second flash of the

image, “how many, how did you know? did you know it before I flashed it the second time?” I

would imagine most would do 10 + 2 very quickly and know it before the second flash. Could

be cool to ask how we could use 14 counters in the next image and have them design the

14th.”

After chatting with Elham, Graham, and Andrew, it was interesting to see the different ways we each looked at the images. (Joe Schwartz conveyed his thoughts to Graham, so I was able to hear those as well) There were distinct differences of when the color of the dot mattered to each of us and when it didn’t as well as a difference of how we arranged the dots to make them easier to count.

These were the things that jumped out at me when I counted each one…

Image 1: Color of the dots mattered. I saw red and yellow, 4+5=9. The arrangement made no difference to me.

Image 2: Color was irrelevant to me. I squished it together to make is a 3 x4 array with one missing. Arrangement mattered here and I built up to the total.

Image 3: Again, color irrelevant to me. I saw the array and subtracted out the missing parts.

Image 4: I didn’t know what to do with but the colors played an important way in which I saw the total. I needed to have those reds to easily see how many missing dots I had to subtract out from my total. So in this one arrangement and color both mattered.

Now, in planning to use this with a third grade class who have not officially started their unit on multiplication and arrays, I was curious most about how they would approach the 3rd and 4th image. Because I wanted to push them to be thinking about combining without having to count by ones, I decided to do them as quick images where I flashed the image for about 3-5 seconds and then covered it back up. I did that twice before taking any answers. In the 3rd image, I wanted to see if the colors of the counters made any difference to them or the arrangement was more important. How did they see the dots and how did they combine and then talk about the way they combined?

The 4th image, I will be honest, I didn’t know what to do with it at first. I knew I couldn’t spend the entire class period with it up there because it was a part of a number talk that I wanted to take about 15 minutes. I had to think about what I really wanted to see the students thinking about when looking at the image. Four things came to mind…

Could they come up with an estimate after one flash of the image or two?
What did they look for when given two flashes of the image. Were they counting rows and columns like the work they would soon be doing in the array work of the multiplication unit?
What did they look for on the second flash? Were they looking for the missing pieces first or second?
Could the students be metacognitive to think about what they were doing each time the image flashed and understand how they counted each time?

I had the chance to go into the classroom, do the Quick Images and film it! Because of time and length of this post already, I am going to leave you with this planning stage and post what I saw tomorrow!

In the meantime, you can play around with what you think 3rd graders would do with these images OR suggest other ways we could use them at various grade levels!

To be continued….

3rd Grade Multiplication Talking Points

10 Replies

This week I had the chance to work with a third grade teacher, Andrea! Her class is just about to begin their unit on multiplication and division so she wanted to do Talking Points to see what they knew, and were thinking about, in relation to these operations. During our planning we discussed the ways in which this Investigations unit engages students in these ideas, misconceptions students typically have, bounced around ideas, and played with the wording of the points. Being my first talking points activity with third graders, I was so excited to see how students engaged in the activity. I have found that even during Number Talks, the younger students are very eager to share their own ideas, but listening to others is difficult.

In looking for how students “saw” multiplication and thought about operation relationships, we designed these Talking Points..

Andrea introduced the activity and we did the first talking point as a practice round in which we stopped the groups after each of the rounds to point out the important aspects. We pointed out things like,”I liked how Bobby was unsure and explained why,” and “I liked how everyone was listening to Becky when she was talking,” and “I thought it was great proof when Lily drew something really quick to support her thoughts.” Then we let them go and walked around to listen as well!

During the Talking Point round, some things we found really interesting were:

How difficult is for them to sit and listen to others without commenting. Not like it is not hard for use as adults though, right? 😉
How much students struggled to say why they were unsure. Sometimes it was not knowing what the word division meant, yet they struggled to articulate what it was within that talking point that was confusing them. What a great thing for them to be able to think about!?
How they related the dot images they had been doing in class to multiplication and division.
How they thought about inverse operations. They said things like, “I don’t know what division is but if I can use subtraction with addition, I probably can use division with multiplication.

We had pulled two of the points that we wanted to discuss, whole group, afterwards, “I can show multiplication as a picture.” and “We can use multiplication problems to solve division problems.” We put them up and just asked them what their table had talking about. The conversation was amazing. Hearing how they thought about multiplication as groups of but 50 x 2 means “fifty two times” while 2 x 50 means “2 fifty times.” We also heard how someone at their table had changed the way they thought about something. And the division conversation was so great and for the students who were unsure because they did not know what division meant, it felt really organic to come out that way… from them, not us.

Of course, we followed with a journal write:) We gave them three choices to write about…

I was so impressed by the way they wrote about their thinking, by 5th grade, they will be amazing!!

The student above, during the Talking Points, said that he could show multiplication as a picture because “an equation IS a picture.” It was lovely to see him make the connection to a visual for an equation in his journal.

I wish the quality of this picture was so much better but her pencil was so light it was hard to see! She does a beautiful writing about how exactly someone at her table changed her mind with such an articulate way of talking about multiplication and division!

This student above explains perfectly why teaching is so difficult…”…sometimes we have facts about math, we all have a different schema. We were taught differently than other kids.” I am curious to hear more about her feeling about the end piece, “some kids know more then other kids.” Is that ok with her and she understands we all will get there just at different times?

These last two were two different ways in which students reflected on the dot images they have been doing in relation to multiplication!

What a great class period! I cannot wait to be back in this class to see how students are working with and talking about multiplication and division!

~Kristin

Fraction/Percent Equivalents

3 Replies

It goes without saying that I miss talking 5th grade math with my students each day. But I am so lucky this year to have a new, wonderful teacher in 5th grade who lets me plan and teach some lessons with her! This lesson was one of her first lessons of Unit 4, Name That Portion.

Since in 4th grade the students do a lot of work with comparing fractions, we designed a Number Talk string in which students were comparing two fractions. We wanted to hear how they talked about the fractions. In the string we used a set with common denominators, common numerators, and one unit from a whole. On each problem we were excited to hear talking about the “size of the piece” being the unit and the numerator telling us how many of those pieces we have. Our 4th grade teachers really do a beautiful job with this work. They also used equivalents to have common denominators to compare and a few used percents, since they had done a some grid work with that they day before.

We started the lesson by asking them how they could shade 1/4 on a 10×10 grid. The majority of the students split the grid in half vertically and then again horizontally and shaded one quadrant. We heard a lot of the “1/4 is half of a half.” As I was walking around, I heard a pair talking about shading a 5×5 in that grid. I saw this as a beautiful connection to the volume unit they just completed in which they were adjusting dimensions and seeing the effect on the volume. I had her explain her strategy and wrote 5 x 5 under the 10 x 10 that was up on the board already and asked how that could get us 1/4 of the whole thing? One student said it looks like it should be half of it because 5 is half of 10, but then one student said since we were taking 1/2 of both it would be a fourth….this is where I hope Leigh (the 5th grade teacher) and I remember to use this when they hit multiplication of fractions!

They then worked in pairs to shade 1/8 and 3/8 and we came back to discuss. We noticed as we walked around that the shading was wonderful on their papers, but when asked to write the fraction and percent, most were blank. I remember this lesson from last year during decimals where the same thing happened. So, we asked them what they thought the fraction was as we got these three answers…

12 r4/100

12 1/2/100

12.5/100

They were not overly comfortable with any of them so we asked them to journal which one “felt right” to them and why…

We loved to see what they knew about decimal fraction relations, but we especially liked the “it sounds more fifth grady to use 12.5.”

-Kristin

My Week In The 2nd & 3rd Grade Math Classroom

13 Replies

While I am loving my new role as the school math specialist, I am definitely finding that my blogging has taken a bit of a slide. I have come to realize that my main inspirations for blogging is having a class every day in which I am thinking things through with and the student work that is the result. Working in various classrooms around the building does not offer that consistent look at student work, but I am SO excited to see so many teachers in my building using student math journals! I think they are finally starting to get used to me snapping pics of all of that great student work at the end of class!

This week, I had the chance to plan and teach with second and fifth grade teachers and do number talks in 3rd, 4th and 5th grade classrooms! Ahhhh…finally student talk and work that gets me excited to learn and inspires me to blog!:)

Second Grade:

Our second grade begins the year with Unit 3 of Investigations which centers around addition, subtraction and the number system. What the teachers and I realized, during the lesson we planned, was that, while the students did an amazing job adding and were finished fairly quickly, they all used primarily one strategy and if they did use a second one, they did see it as different.

The majority of the students decomposed both numbers and combined the tens and ones like the top two strategies of this student:

When asked to show another way, he quickly did the third strategy. Walking around the room, the teacher and I saw many others thinking in the same way as the third strategy but intricately different.

Thinking in terms of the 5 Practices, we monitored and selected a progression of papers to elicit connections between strategies, however what we found is that as students shared, the others were saying, “I did it the same way, I just broke it apart.” They didn’t see a difference in breaking both numbers or breaking one number or then how they thought about the decomposition and combining of the partial sums. We left class with that spinning in our heads….”It is wonderful they can use a strategy to add, but how do we get them to see the differences in each and think about when one may be more efficient than another?” and for me, being new to second grade math, “How important is it that they do? and Why?” The following class period, which I could not be there due to a meeting, the teacher began creating an anchor chart of strategies as students discussed them and pushed them to see the similarities and differences of each. I am still thinking through the importance of these connections and realizing I have so much to learn!!

3rd Grade

In third grade this week, I was asked by a teacher if to come and do an addition number talk with her class. That took no thought, of course I jumped at the chance to chat math with them! I realized both before and after how much easier it was for me to plan for my 5th graders because I knew them and, due to experience, could anticipate fairly well what they would do with problems. I chose a string of addition problems that, while open to any strategies, encouraged the use of friendly numbers. I forget the exact string now, but something like 39 + 43 and 53 + 38. After being in second grade a few days before, it was interesting to see the same decomposition of both numbers to tens and ones and recombining of them. I am beginning to think that is the easiest, most instinctual way for them to do problems because they CAN do it other ways, they just jump right to that first! We did three problems together, and while the use of friendly numbers did emerge, it was definitely not the instinctual choice of the class. I left them with one problem to do “as many ways as they could in their journal (WOOHOO, they have math journals). I went back later to have them explain some of their strategies and take a look at their work.

I was excited to see that while many started with tens/ones, they had a wide variety of thinking around the problem:

Of course there are always a couple that leave you thinking….

In his verbal explanation, this one said he, “Multiplied 35 times 2 because he knew that 30 and 30 made 60 and the two 5’s made 10 so that was 70. Then he added the 14 to get 84.” When he first started talking, I had no idea where he was going and was honestly prepared to hear an incorrect answer at the end. I asked him to write out his thinking and he gave me this great response:

I know we need to be aware of his use the equal sign and make that a point in future number talks, but that thinking is soo interesting. He saw he had two 35’s, one of which within the 49 and then 14 leftover once he used it in his multiplication. Great stuff!

This one I need to hear more about from the student. He said he subtracted from 100 on a number line to end at 84. I asked him why he subtracted and he said he knew he needed to get from 100 to 84. I was confused but in the midst of the class, I didn’t think it was the time to go deeper with this one. I can’t tell if it is connections to things they are working on in class with 100 or something else?

I still have to blog about the 4th and 5th grade fun, but this is getting long already! I will save that for tomorrow!

~Kristin

Lunchtime Cafeteria Chat

8 Replies

It is amazing to me what a well oiled machine our cafeteria is each day! Amidst the near 800 students walking in and out, the volume of students all talking over one another, the perfectly timed staggered schedules, the forgotten utensils, and spilled food and drinks, the students still get in and out of there within 30 minutes each and every day without fail. The wonderful people working those lunches are absolutely amazing!

As I walk around the cafeteria, or even stand outside in the hallway, I hear all of the different types of conversations…some are about their lunches, or about their classes that morning, or possibly even about their classmates. However, at a glance around the cafeteria, there are other students who are not talking at all and some tables are even eating in silence. While I appreciate students who may want to eat in silence, I wonder if there are others who need a topic in which to engage in conversation?

When my colleague Erin suggested putting up some type of slide presentation on the projector screen on the stage during lunch, I thought it was a genius idea! She said it could be like the previews in a movie theater that everyone watches before the feature presentation. Like most ideas with me, we jumped right in. We came up with prompts for students to use as a piece of their conversations and spark interesting conversations around the cafeteria. We put 15 ideas together in a looping ppt, with a 30 second transition between slides.

Here are our first week’s slides:

It was so fun to walk around and see students pointing at the screen and offering what they thought the answer would be and explaining why! What a way of creating a student culture that demonstrates how differently and creatively we can all think about the same thing.

Like any idea, there are always ways to improve and this idea is no different! We have brainstormed ways to include pics of the students, our Peacemaker awards (shout outs for students and/or teachers who are caught doing great things -PBS), pics/fun facts about the teachers, and ways for all of the students to contribute ideas/prompts for the presentation. My colleague Melissa came up with the adorable name of “Chat-n-Chew” which is so much better than “lunch presentation” and offered to have a group of her students design future presentations and of course, they are the “Chat-n-Chew Crew.” 🙂 Each homeroom teacher will have suggestion forms for their students to send to Melissa’s 4/5 class to use in their presentation creation.

One day, I will get Erin on here to blog (I hope she is reading this) because she has so many wonderful ideas to share! 🙂

-Kristin

MathMinds

by Kristin Gray.

1st Grade Dot Addition

Kindergarten Number Lines

How Planning Mistakes Can Lead To Great Student Thinking….

3rd Grade Dot Image Number Talk

5th Grade Fraction Clothesline

Dots, Dots, and More Dots…the Planning Stage

3rd Grade Multiplication Talking Points

Fraction/Percent Equivalents

My Week In The 2nd & 3rd Grade Math Classroom

Lunchtime Cafeteria Chat