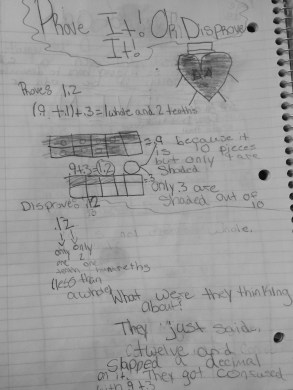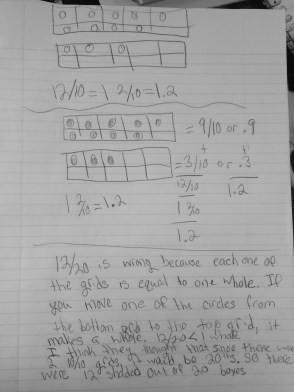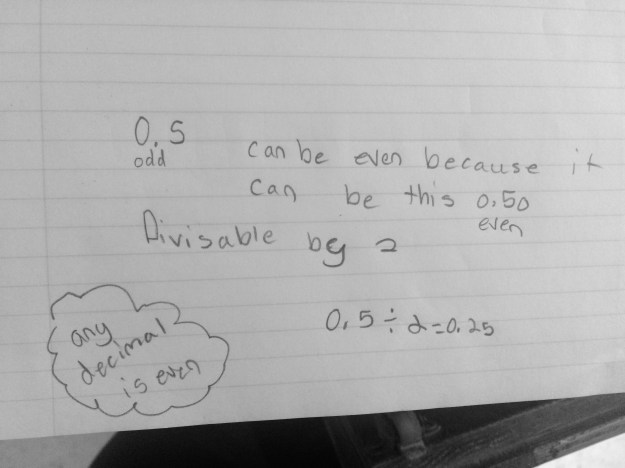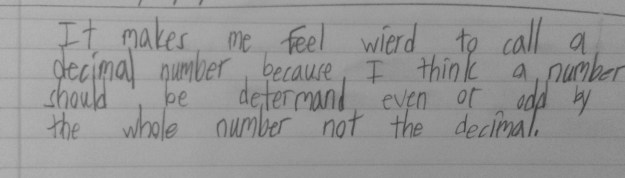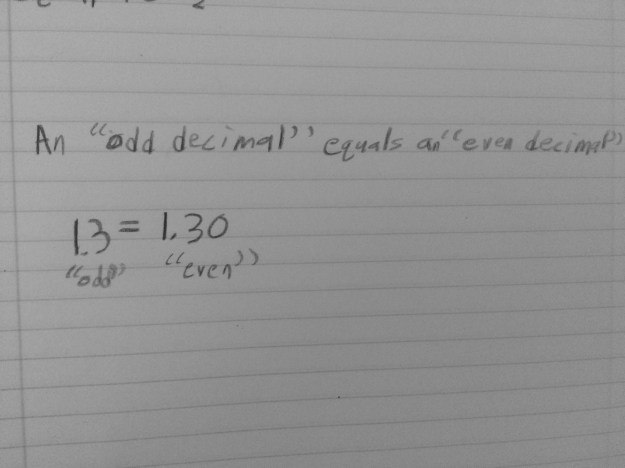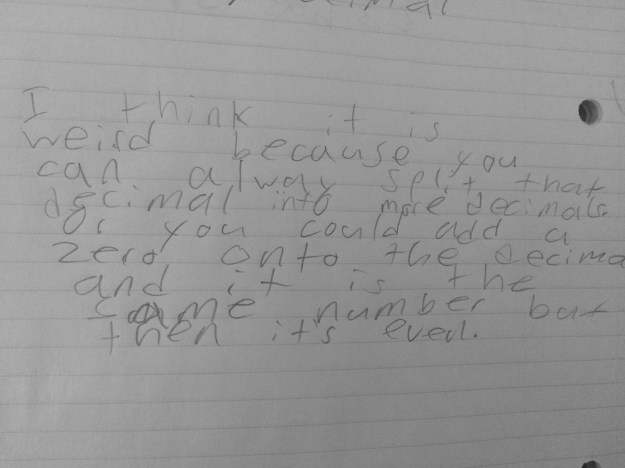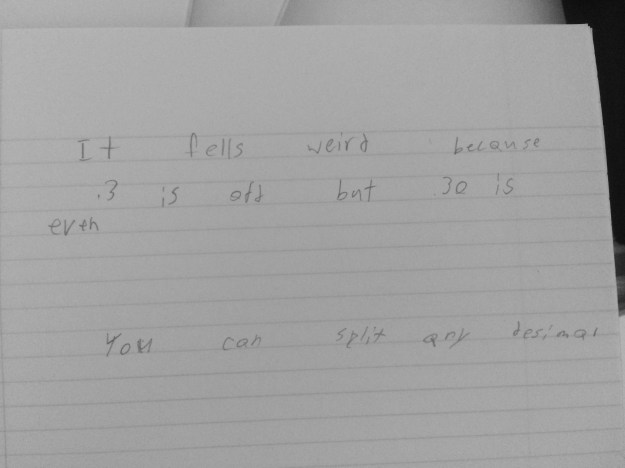My colleague Nancy and I facilitated a K-2 afternoon professional development session yesterday afternoon. The 2.5 hour session was with a wonderful group of teachers from across our state who we are fortunate to work with several times over the course of the school year. Our major focus over the course of this school year centers around connecting arithmetic to algebra based on a book by Virginia Bastable, et al, that I blogged about here: https://mathmindsblog.wordpress.com/2014/11/20/articulating-claims-in-math/ I thought blogging about this experience would be helpful for any of our teachers who could not attend and for any others who facilitate PD.
I find planning for professional development is much like planning for the classroom. Many of the same questions arise:
What content will be engaging and relevant? (especially being an afternoon session when everyone is winding down on a Friday)
What is the trajectory of the content?
Where are they? Where are they heading?
What questions or prompts will encourage conversation?
When are points for table conversation? Whole Group conversation?
How will be know where they are in terms of the content when they leave us?
How will we follow up?
After much planning, videoing, and organizing this was the flow of the afternoon:
We opened by getting into grade level groups to discuss the homework from last month, doing a group planned Number Talk with their students. They used this form to plan together and brought back recording sheets of their work to discuss these two questions:

 With the number talk being planned by the group, I felt a sense of ownership over the results in the classroom and, really, who doesn’t like talking about all of the wonderful things our students say during a number talk?
With the number talk being planned by the group, I felt a sense of ownership over the results in the classroom and, really, who doesn’t like talking about all of the wonderful things our students say during a number talk?
We continued with a quick recap of last month’s session on the book, “Connecting Arithmetic to Algebra” to plant the seed for our routine of focus that day, What Do You Know About….?


 Now into the really fun stuff! Working with a Kindergarten teacher in my school (@jennleachteach) who is also a part elementary pd group, we planned and videoed a math routine called “What Do You Know About 15?” in Jenn’s class.
Now into the really fun stuff! Working with a Kindergarten teacher in my school (@jennleachteach) who is also a part elementary pd group, we planned and videoed a math routine called “What Do You Know About 15?” in Jenn’s class.
We mixed the grade level PD groups up at this point so there was a range of K-2 teachers (and a few math coaches) in each group. They got a blank planning sheet to brainstorm what they think the planning would look like for this routine in a Kindergarten classroom in January. It was great conversation, with the Kindergarten teachers being the experts at each table. I thought this was such an interesting dynamic since we often tend to pose a mathematical idea and ask what previous understandings K-2 need to build to get there, however, with this opportunity, it was starting in the opposite direction and really focusing on what Kindergartners know at this point of the school year.
 After they predicted what our planning sheet would look like, Nancy brought 6 teachers up to act as students in a fishbowl enactment of the Number Routine. The other teachers in the room were observers focusing on two particular aspects of the talk, what you notice about the teacher recording and what you notice the “students” noticing. Importance of recording was a previous topic in an earlier pd, so we wanted to be sure that resurfaced. Nancy did the routine with the teachers and we came back as a group to discuss the observations of our focus questions. Our discussion also touched on the use of the talk moves she used to clarify and illustrate student thinking.
After they predicted what our planning sheet would look like, Nancy brought 6 teachers up to act as students in a fishbowl enactment of the Number Routine. The other teachers in the room were observers focusing on two particular aspects of the talk, what you notice about the teacher recording and what you notice the “students” noticing. Importance of recording was a previous topic in an earlier pd, so we wanted to be sure that resurfaced. Nancy did the routine with the teachers and we came back as a group to discuss the observations of our focus questions. Our discussion also touched on the use of the talk moves she used to clarify and illustrate student thinking.
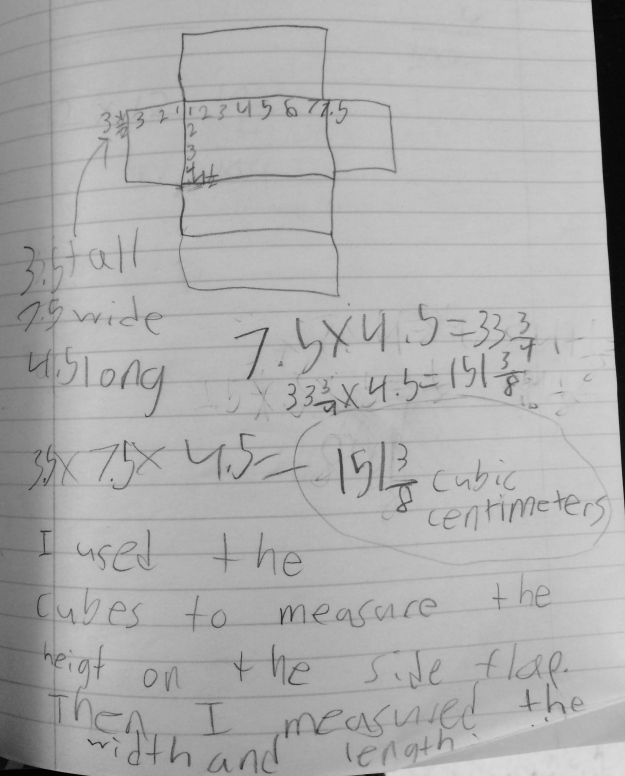
We then watched Jenn’s Kindergarten class do the same exact Number Routine, focusing now on the follow up piece of the planning sheet. What did they notice the students noticing? I wish I had permissions from everyone because Jen did a beautiful job in facilitating the talk and her students said some amazing things. We also took a look at the planning sheet that Jenn, Nancy and I had done for this routine. Here is the planning sheet and anchor chart that arose from the talk:


As a group we discussed what they noticed the students noticing that could lead to future “claims” in their classroom. Teachers noticed such things as, “We can count by fives to get to 15” “It is three fives” (of course I am thinking about groups of and multiplication right there!) “A teen number is a group of ten and some more” “Looking at equality with related equations” and “The 1 means one ten”
Jenn then gave students “random” journal entries to see how students were thinking about the numbers after the talk. To differentiate, we decided to give students 12, 19, or 21 depending on where we thought their entry level was into this thinking. After students completed the journals they chatted with someone who had a different number, to talk about their ideas.” Here are the student samples our PD group looked at and discussed:






 We ended with Virginia’s conclusion slide about Connecting Arithmetic to Algebra and our homework for the group:
We ended with Virginia’s conclusion slide about Connecting Arithmetic to Algebra and our homework for the group:

 We also gave an Exit sheet to help us in future planning. We got some very useful information as to where the teachers feel they are. I am very excited to hear about everyone’s journey back in their classrooms next month!
We also gave an Exit sheet to help us in future planning. We got some very useful information as to where the teachers feel they are. I am very excited to hear about everyone’s journey back in their classrooms next month!


 -Kristin
-Kristin
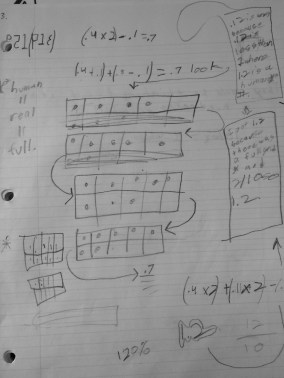
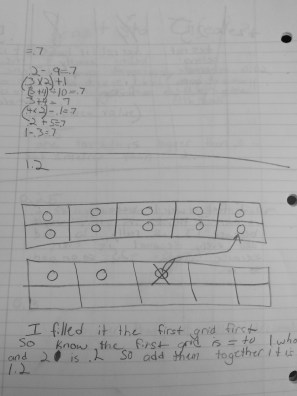
 I think put up two frames, one with .9 and the second with .3 and asked students to write down how much was represented in the picture. Like last year, it was a mix of 1.2, 12/20 and .12. I asked students to prove the one they got as their answer and then explain where they think someone got confused with one of the answers they do not agree with. They did a beautiful job with this.
I think put up two frames, one with .9 and the second with .3 and asked students to write down how much was represented in the picture. Like last year, it was a mix of 1.2, 12/20 and .12. I asked students to prove the one they got as their answer and then explain where they think someone got confused with one of the answers they do not agree with. They did a beautiful job with this.