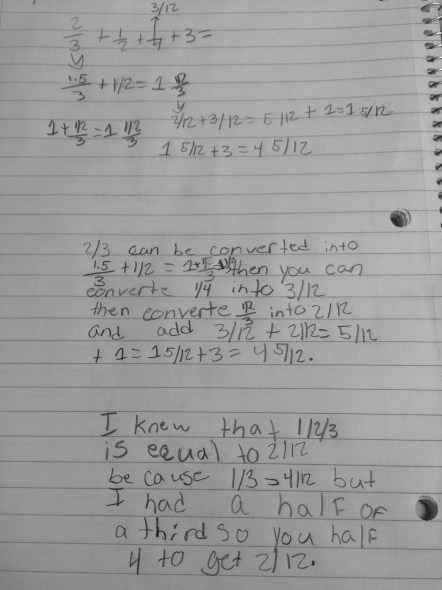Category Archives: Math

Always, Sometimes, Never….Year 2, Part 2

Always, Sometimes, Never….Year 2

Last year, I used this activity with my 5th grade students and blogged about it here. This year, I used the same activity, however tried it a bit earlier in the unit than last. Based on our Talking Point activity before the unit began, I found the students had very good understandings that would emerge naturally in the Always, Sometimes, Never activity. I wanted to see how using the activity before a lot of our classification work would affect the outcome, if it would differ from last year’s.

This year, we had played “Guess My Rule” the day before in which students use attributes to choose two quadrilateral cards that fit their rule and one quadrilateral card that does not, while their partner tries to guess the rule. It is great for thinking about classification by sides or angles and vocabulary building. At the end of class, we did a few rounds together, and chatted about some vocabulary that was helpful and talked about our classification by sides, angles, or both.

Being the day before Thanksgiving, you never know how it was going to go, but they were so engaged in the work. Here is a copy of the cards that I used:

I gave them time to individually read them and underline any words or wording in which they needed clarification. Although I was surprised that some students asked about words we had discussed in prior class periods, I was so much more happy they felt safe enough to ask for clarification. This is a prime example of not making assumptions in what our students know just because we have talked about it before in class.

They cut them out and went to work. As expected, they would have a brief conversation with their group and place them quickly into the appropriate column on their desk. I let them do that on my first round around the classroom and then as I heard some debates starting, I suggested that maybe using their journals to show their proofs may help their argument. For those who were quickly done, I said, “If it falls in the Sometimes category, you should be able to show when it does happen and when it doesn’t happen, right?” I also pointed out the reasoning for Always never being able to be disproved and the opposite for Never. This had them really go back and take a deeper look at the cards and got their conversations going.

Of course, we did not get to come back together as a group and come to consensus but here were the table card arrangements as the class ended:

I had them do an individual reflection on which card they are still really struggling with and these responses are going to help in framing how I proceed from here on Monday after vacation:

It is really interesting that for some students the orientation of the shape makes the biggest difference, others strugglw with the vocabulary, and, like last year, that rhombus one is blowing their minds. It is so interesting to me that a student can apply shape attributes to make a conclusion that a rhombus is a rhombus, but then to take that reasoning and apply it to another shape, is extremely difficult. This led to a very interesting conversation between a colleague (who was in observing) and myself about students knowing definitions versus descriptions….still wrapping my own head around that one…will probably be a blog post coming soon:)

With all of this information from the students, on Monday, I plan on putting them in groups based on the related cards they were left grappling with. I think rearranging the groups will lead to interesting conversations and more detailed proofs. Each table will get three cards to create an argument for the placement of that card. They will present their argument to the class and we will try to come to consensus as a class. Last year we did this share as a whole class, and I didn’t feel like it “wrapped up” and things were left hanging out there that needed to be a bit more solidified in future classification work, so hopefully this will be change that.

Happy Thanksgiving all!

-Kristin

Talking Points – 2D Geometry

9 Replies

We are about to start out work with Polygons, so I decided to kick it off with Talking Points. If you have never read about them before you can check out my post or Elizabeth’s post to learn more.

Here were the points my students were discussing:

I had gotten these points by looking back at their fourth grade geometry unit work and thinking about what misconceptions or partial understandings students have each year when we start this unit.

This time, I made a few changes from past experience. In each group I had a facilitator to be sure that everyone got a chance to speak without interruption during Round 1, and a recorder to keep the tally for the group. Also, after the first talking point, I had advise from a math coach in the room filming with me to add individual think time after the reading of the point. LOVED IT! During think time, they were jotting in the journal and getting their thoughts together. I got things like this from just the think time:

It was nice to see them take ownership with their journal without being told to write anything down. They were working on proofs before they started. After the six talking points, I posed three questions on the board for them to reflect upon individually:

1 – What talking point are you sure you were right in your answer? Explain your reasoning.

2 – Which talking point are you unsure about your answer? Why?

3 – Which talking point did your group agree upon easily? Why do you think it was easy for your group to agree on that one?

Here are their reflections:

Never anticipated so much “left angle” talk in my life 🙂 I learned SO MUCH about their understandings and wish I had time right now to add my comments to each journal, but I will very soon!

So, I have a moment here at lunch to reflect on what I learned from these talking points:

TP1 – As I anticipated, this one is always a source of confusion. Every year it seems as if the students know the sentence goes one way or the other but can’t remember it because there is little understanding of the WHY piece. Later on in the unit after we have done more classifications, I do more of these statements with Always, Sometimes, Never, so this is a something I wanted to see how students were thinking about it. Most tables said something to the effect of “I remember last year we said a square is a rectangle or a rectangle is a square, but I can’t remember which one.” Another conversation I heard was that a rectangle has to have two short sides and two long sides.

TP2: I loved this question and was really pleasantly surprised to see some trying to draw it and ending up with unconnected sides. One thing I was so surprised about was the “left angle.” They were not thinking the degrees changed so much from the left to the right angle, but more the orientation of the angle (left side, right side). Interesting.

TP3: I got a great sense that most students knew what area and perimeter were and the best part was that if they didn’t remember, someone at their table did and gave an example. Regardless if they knew they could be the same, I was excited to see a great understanding from most here.

TP4: This one was great. I saw some students drawing a square on their paper, showing the group, rotating the paper and saying, “See, now it is a rhombus.” They all seemed to be in the mindset that a rhombus is a diamond shape, but really not reasoning about the attributes that make it a rhombus.

TP5: They did a very nice job with this one. A lot drew examples of combining two shapes, while I heard others asking their group if the “inside connected side counted” when they were trying to name it. Also realized that the term polygon was not familiar to most students. I am wondering what they called them in earlier grades? Pattern Blocks? Shapes?

TP6: Interesting one here and it is where we start our 5th grade work with polygons, classifying triangles. Again, the left angle reappeared:) I did hear a few struggling with the name of the angles, obtuse, acute, right but then I had some that said there are other 3-sided shapes that aren’t called triangles. Hmmm, can’t wait to find out what they are! Of course, you always have your comedians who say agree because it could be Bob or Fred.

Can’t wait to start planning this weekend!

-Kristin

What Happens When You Divide by Zero?

Volume with Fractional Dimensions

2 Replies

Before I began our volume work this year, I blogged about my planning process here: https://mathmindsblog.wordpress.com/2014/10/20/unit-planning/. As anticipated, I had many students who quickly developed (or already had) strategies for finding volume and could articulate a conceptual understanding of what was happening in the prism. In my previous post, I was throwing around the idea of giving those students dimensions with fractional length sides, so the other day I thought I would try it out. I did this Illustrative Task as a formative assessment of student understanding. Many students were done in a couple of minutes, with responses for part b that looked like this:

As I walked around the room and saw they were finished quickly, I asked them to revisit part b and think about a tank with fractional dimensions. Because of the great work they had done here I thought they would have some interesting thoughts. These are a few of the responses I got:

So, what did I learn from this work? I saw they had some great understandings about taking a fraction of one factor to make a number that they knew they needed to multiply by a third whole number factor to get 240. In the first two pictures, there is a great pattern happening that I want to explore further with the whole class. I also loved seeing that a student took the question “fractional length sides” to include decimals in his work. In my question, however, I had wanted them to consider more than one side in fractional lengths, however not being more explicit, they took it and ran with one side being fractional. In the next lesson, I thought I would push them a bit with this.

In the following lesson, students were finding the volume of an unmarked prism in cubic centimeters. They had rulers, cm cubes, and cm grid paper available to them, and went to work. Every year this happens, the Investigations grid paper works with the box to be whole number dimensions, however the cm are a bit “off” when using a ruler or cm cubes. I knew this, however, I do love the discussions that evolve from students who used different tools. I also thought this is the perfect opportunity for my students who were beginning to think about fractional sides. What transpired in the whole class lesson is a blog post in and of itself, however this is what came about from the fractional sides work…

Sooo much great stuff here! I had a group who was using the cubes, coming out with halves, but not wanting to round because it was “right in the middle” of the cube. I let them go and came back to see they were multiplying whole numbers, multiplying the fractions, and then adding them together to get their product. I asked them to think about another multiplication strategy to see if they got the same product, then came the array. Another student in the same group solved mentally to get the products. Unfortunately, the class had to leave me to go to their next class, also leaving me with so many things to think about. From here, I want to be sure students start to think about reasonableness of their solutions, compare their fraction multiplication strategy to whole number multiplication strategies, and think about how we multiply three numbers (Associative property). So much to do, I need full day math classes!

-Kristin

Volume Student Work…

5 Replies

So, I couldn’t resist the urge to blog about my students’ first day of work with volume since I had posted the other day about my planning,even though I have tons of other things that need to get done. We are sharing their work tomorrow to elicit strategies and make connections. With the 5 Practices in mind, I am heading off to sequence the shared work to make those connections.Tons of things to work with here!

As always, I love your thoughts on the order and items you would share!

FOLLOW UP – For homework, I had the students try to generalize a strategy for finding the volume of any box and here are a few that I got and plan to build upon…

Unit Planning

3 Replies

This week, I am starting our next unit in Investigations, Prisms and Pyramids: 3D Measurement and Geometry. Every time I start a new unit, I always like to read the Teacher Notes in the back of the teacher’s book because Investigations has done such a phenomenal job explaining students’ work prior to that unit, the big mathematical ideas, student misconceptions (with dialogue boxes), and offering examples of student work for both the activities and assessments. It is an invaluable resource that often gets overlooked. After reading the teacher notes, I typically like to look at the Ten Minute Math Activities, build my Number Talks, and then dive into planning out the lesson activities. I was going to devote this entire post to thinking about this unit on Volume, however I tweeted out suggestions for a blog topic on this flight and Michael gave me this:

I feel like I just finished up such an exciting (in my mind at least 🙂 blog post about student moments with multiplication of fractions that I wanted to do something a bit different and this tweet gave me an idea. Since my students have done such amazing work with fractions, I started thinking about how I could embed that into our volume unit. So, after reading the Teacher Notes, instead of jumping into the number talks right away, I began reflecting on those great fraction moments and putting them in the context of volume.

Our first activity in the unit is building boxes, estimating how many cubes will fill the box and checking that estimate by physically filling the boxes with cubes. We then share and discuss strategies for finding the number of cubes as a class. I find every year, I have over 1/2 the class who can see the layering and arrive at an efficient strategy including length x width x height fairly early in the lesson, while others cannot visualize how to organize the cubes. They can easily find the number of cubes in a rectangular prism when the box is constructed and filled, however moving to a net or just dimensions is a very tough abstraction.

I think one of the hardest aspects of teaching is meeting every student’s needs on a daily basis. This is one of those lessons in which I feel I struggle a lot. It is beyond the numbers and context and more about the students who have the spatial reasoning to abstract volume vs those who need to always build the box to arrive at an answer. For those who need concrete models, I feel comfortable meeting their needs through using cubes and building on that concrete work to form generalizations for finding volume. However, what can I do for those who just “see it” and building those boxes is unnecessary and a tedious waste of time? They are done the lesson in like 10 minutes and are waiting to share while others build. Bigger numbers won’t challenge them, they can prove it always works, doubling/tripling volume is a class lesson after that one…..hmmmm….

This is where Michael’s tweet made me think about our fraction work. I have never done my fraction unit before volume unit before. Typically we do volume to start the year and then move into fractions. I think it is so interesting to think about those students who can reason about fraction multiplication and how they would think about a volume problem in which there are fractional dimensions. What does the picture look like? How can you have a 1/2 in x 1/2 in x 1/2 in and end up with 1/8 cubic inch? How do you end up with a smaller fraction than all of your dimensions? That is a tough concept to grasp and I THINK THAT WOULD BE SO COOL for them to think about!

Now the even harder part comes into play, planning to launch that with them. Questions I have to think about (and any/all thoughts are always welcome):

– Do I build on the problem with whole numbers (2 x 3 x 4) and ask, what would happen if that was 4 1/2 tall instead of 4? Would it increase the volume? How do you know?

– Does it make it harder or easier to manipulate a certain dimension, i.e. length, width, height?

– Do mixed numbers feel like a good starting point vs fractions less than 1?

– What will their recording look like? What are good questions to ask them when they have found the answer?

– Is there a better volume model aside from cubes (which you cannot break in fractional parts to prove your point)?

….and there are probably a million more, but the flight is about over….so much planning left to do. Not to mention the actual typing of my lesson plans and 9 million other things I should be getting done while I type this blog! I just love to write about this stuff…cannot help myself! I apologize for any typos, no time to re-read before saving and putting the laptop away!

-Kristin

“Is this really just multiplication?”

7 Replies

After a couple of weeks working with problems in which they were taking a fraction of a fraction, fraction of a mixed number, the students made some conjectures about the problems.

We went through each one, proved, disproved and refined them when finally one student just asked..

“Ok, isn’t this really just multiplication?”

I knew he just wanted an answer, but that was not going to happen. 🙂 Since we have been doing a lot of multiplication number talks, I thought I would see if I could make a connection to whole number operations.I said, “Well, if it is multiplication, do you think the strategies on our anchor chart should work for the fractions too?” We made the anchor chart as strategies arose in our number talks. I put 2 1/4 x 1/2 on the board and said, “Try it out.”

They worked in groups and came up with some pretty amazing stuff…(A couple students chose to try a different problem, so the sampling below may be a mix)

We are going to share some strategies tomorrow since the rest of the class period consisted of them “arguing” about fraction multiplication. It made my day when one of the girls was leaving my class and said to her friend, “That was so fun!”

Wait, fractions fun?? LOVE IT!

-Kristin

Lesson Study: Teaching “Take 2”

4 Replies

Every week, I read so many wonderfully open and honest math blogs from my tweeps, the majority of them found on this list. The blogs span across grade levels, mathematical content, teacher experience, and more impressively, the world. Whether it is a good, bad or ugly lesson, after reading the blogger’s reflections and colleagues’ comments, I am always left with the feeling that if, given the chance to do that same lesson just one more time, there would be significant improvement. Whether it be the organization of the lesson, management of the materials, questioning of the students, sharing out of responses, the task itself, or any of the other countless components of just one math class period, sometimes we all just need someone to say “Cut” on Take 1 and allow us the opportunity for a Take 2. With multiple math classes a day, we often get the chance to adjust a lesson between class periods, however there is not a second chance on that same exact lesson until the following year, nor a significant amount of time to make dramatic changes. I am not saying that we don’t revisit, learn and improve from that point on, however, how amazing would it be to erase a lesson that didn’t go “quite as planned” from a student’s memory and make it even more meaningful for them on our second take? Wouldn’t it be great to answer all of our “What ifs”?

When selected to participate in the project I blogged about here, I had the idea that it could work as a type of lesson study. Since Alicia and I were both 5th grade teachers working on fractions at the beginning of the year and planning a common task, I thought it would be interesting to see how our work together could go above just collaborating around the lesson development to actually creating a “perfect lesson”…or as close as we could possibly get to it. This lesson study would be unique in the sense that all of our work and observations would have to be virtual due to the distance between us. After all of our planning around the 5 practices, our team of Jody, Chepina, Alicia and her math coach, Jennie, decided that I would teach the lesson first, they would all observe the video (through Teaching Channel Teams), we would look at my student work and from there make adjustments for Alicia’s lesson. Being super critical of my own practice in general, it was fairly simple for me to make suggestions for improvement.:)

THE TASK: Part 1: The 5th graders want to raise money for their overnight camping trip by selling cornbread during the school district Chili Cook-Off contest. All of the cornbread pans are square. The first customer, Mrs. Farmer, wants to buy 1/4 of a pan of cornbread that is 1/3 full. What fraction of the whole pan does she want to buy? Part 2: The next customer is the elementary school principal. He wants to buy 5/6 of a pan of cornbread that is 1/2 full. What fraction of the whole pan does he want to buy? Each part also had a part b asking if the pan costs $12, how much would they pay for their piece.

MATHEMATICAL GOAL: Students will develop mathematical generalizations connecting previous understandings of whole number multiplication to multiplication with fractions. (Relational understandings)

Just some of my 5 Practices planning for the task:

With that little bit of background, here is a look into the lesson and the adjustments we made to improve…

My Class: I opened the lesson with a multiplication Number Talk. It was our hope that through the progression of problems, the area model would arise to allow for connections to our task, however in a classic case of anticipating gone bad, there was no area model to be found that day. Great thinking around the multiplication, so I wasn’t disappointed in that, but no array.

Alicia’s Class: After collaborating around the video and my reflection, we decided to start with a number talk on fraction of a whole number. Both of our classes have been working on that and thought it may put students in more of a “fraction mindset” of taking a part of something before beginning the task. We designed the progression: 1/2 of 16, 1/4 of 16, 1/8 of 16, 3/8 of 16 in hopes of pulling out thoughts such as: dividing by 2 is the same as taking half (and 4 for the fourth), a half of a half is a fourth (and the same reasoning for the 1/4 and 1/8), as well as big ideas around equivalence and decomposition. Perfect change.The students shared all of the ideas we wanted to bring out, even as far as pushing the decomposition of 3/8 from 1/8+1/8+1/8 to 3 x 1/8. Not in that exact notation but as 1/8 of 16 = 2, so 3 x 2 = 6.The only thing I wish I had seen (simply because I love when students make connections to previous problems in a NT progression) is 1/4+1/8= 3/8, so 4+2= 6.

Timing was great and the lesson was improving already…..

My Class: As I read the problem aloud and used some listening techniques I learned from @maxmathforum, students had individual think time and moved into working in a group. The first thing I noticed in my students who struggled with entry into the problem was the wording of the problem itself, “1/4 of a pan 1/3 full” muddled the whole and was confusing for them. Also, and I have mixed feelings about this, but the first part allowed for students to get the correct answer by subtracting 1/3 – 1/4 to arrive at 1/12. This is not something we had even thought about. I love the conversation that arises from this, especially because it will not work in the second part, however I thought maybe it did lead us astray from our goal for the lesson.

Alicia’s Class: Alicia launched the lesson with an actual pan of cornbread to show the class, most impressively homemade:) It gave the students a nice visual for their models/representations and I think offered access to those without entry. We changed the wording of the task so her task read, “Mrs. Farmer, walks up to buy cornbread and the pan is 1/4 full. She wants to buy 1/3 of the remaining cornbread. What fraction of the whole pan does she want to buy?” and the same type of wording changes for the second part. We also changed the order of the fractions in the first part so subtraction would not happen them upon the correct answer and in this case be an unreasonable answer of – 1/12. Having not anticipated subtraction, which seems SO obvious now…duh, it was nice to be aware that it may show up in her class and adjust accordingly. Again, I love that conversation of why it is not subtraction and will definitely revisit, but for the sake of our goal, this was much improved.

After part 1, we planned to do a quick share of strategies.

My Class: During the share, I selected and sequenced three papers. My initial thought was to share two correct representations and one with a sticking point I noticed showing up on numerous papers. I chose two students to share who had the array correct, but cut a bit differently and then a subtraction student with two separate pans drawn (one with 1/3 and one with 1/4). My hope was to draw out, from the class, that we were just dealing with one pan and get them thinking about if that made sense. However, the share went longer than anticipated so I decided to leave that out there for them to think about and move around to my few who were sticking with subtraction individually with some strategic questions about the whole.

Alicia’s Class: After seeing the lengthy share in my video, we decided to have Alicia choose three students,with correct representations and different labeling/cutting, with the third being a student who is having some numeric notation around where he/she is seeing multiplication. Alicia’s final sharer ended with his representation and numeric notation showing that he multiplied the numerators and denominators to get the answer. He ended his share wonderfully by saying you not taking 1/3 of the whole you are only taking 1/3 of the 1/4. After talking to Alicia and Jennie afterwards, this student has had some outside experience with multiplying fractions in terms of the algorithm, however struggled a bit to connect it to the why. It was nice to have him share and explain his representation.

Now both classes ventured into part 2 of the task.

My Class: I actually enjoyed this part of my lesson, and was excited to see many of my students up and using the fraction bars to create proofs for their tablemates. The biggest obstacle in my class seemed to be naming the piece. I found that after working through the first part and seeing the share, students were more comfortable with what was happening in the problem and could shade the piece the principal was getting. Many were saying the answer was 5/6, 10/12 or 5 pieces. All correct answers, but that fraction of what whole or 5 pieces the size of what? They had great discussion (even a bit of a heated argument between friends) about whether the answer was 5 or 5/6. I love that they left for lunch still arguing about it…nerdy fabulousness. I did my share with students whose representations were a progression of a student who cut the whole pan into twelfths, another who was just half cut but visualized the other twelve and one who solved it backwards at first, 1/2 of 5/6 and their partner explained it to them and redid it. I thought it was a beautiful picture of the commutative property, that even though the order doesn’t matter in the solution, the picture changes.

Alicia’s Class: I felt this part was very similar between the two classes. Her share was nice (and I wish I had done it) because she brought up one of her students who had it wrong to start and was brave enough to get up and say what she tried that didn’t work and then what worked for her the second time after talking with her group. It was beautiful and connected a lot of learners who tried it the same way the first time. She opened it up to the class for a few comments/questions after each sharer. The students were very nice in giving positive feedback as to how easy to understand the representation was and stressed that the labeling made a big difference.

I am thinking it would help in share outs to focus the students more on what we want them to be noticing, as my buddy @maxmathforum says often. For example, since our goal was to bring out the connection to multiplication, tell students that as others are sharing, be looking at their representation and for the operations they used and why they are using them to get their answer. I would love for it to explicitly come out WHY the numerators and denominators are multiplying and the connection between dividing into 6 parts is the same as multiplying by 1/6. Students did say those things but more in a vague-only-the-teacher-picks-up-on-it kind of way, but I think if we focused their thinking, it may come out more.

The ending (If you are still reading at this point, that is dedication)….

My Class: Through our group planning, we decided to end with a journal entry/exit ticket asking students to think about where they saw multiplication in the work they did. We thought bringing their attention back to their work, having multiplication in mind, would push students to think about many ideas such as taking a part of a part results in a smaller answer, the order of the fractions resulted in the same answer and the denominators multiply because you have to think in terms of the whole. So…I did not really get the results we were looking for. Don’t get me wrong, I had some wonderful responses I used to guide my instruction, however many left me with no idea of what they were thinking about the fraction of a fraction work. This was mainly because of part b in each question asking students about cost. They ALL saw multiplying there…you have 5 pieces, each is $1 so 5 x $1 = $5. That really didn’t help me as a piece of formative assessment work. Here are some of the ones more along the line of matching our goal that we used in adjusting for Alicia’s lesson: (sorry about the lightness, my copier at school obviously has some issues)

Alicia’s Class: After reviewing my student work, we decided for Alicia to use a ticket that had a new problem, 3/5 of a pan 1/2 full, followed by the question about multiplication noticings based only on the first parts of each question and the ticket. MUCH better read of what the students understood. Even if they could not see multiplication, students were able to represent the problem and come to a solution. It was more informative in terms of where to start building with that students and where they were in terms of our mathematical goal. It was interesting to find, in reviewing her tickets, that students she and Jennie thought “had it” during the lesson could not do it independently on the exit pass. We went back to their work for the day and they did seem to have the correct work and responses, however how much of that was table work?

That got me thinking how it would be nice to know what student writing was done during individual think time before the group work started. I think next group task, I will have different-colored colored pencils on the table…one color for individual time and then switch colors for group work. Then I may be able to better see a student’s thinking.

My Reflection on the Process: Throughout this entire process, I found myself saying “we did…” and “our lesson…” A LOT. It became not just my lesson that I was planning for my students, or a lesson I was observing to give feedback, but instead a wonderful collaboration in which the entire goal was to make it the best possible learning experience for the students. In planning the initial lesson, there were things that didn’t go as we thought, things we hadn’t anticipated would happen, and connections that we thought would clearly come about, that didn’t. The fantastic part is, we got a Take 2. We had the chance to talk through why things didn’t work and how we can improve for the next take. After a lesson, I am typically left wondering, “What if I had done…,” and although it was not taught again with my students, I got to see that “What ifs” play out…and it was so much better!

I am a HUGE fan of coaching to improve teacher practice and this type of lesson study took it to a whole new level for me. How wonderful would it be to see the lesson I am going to teach play out before I really have to teach it? I am really thinking hard about how this could work in a school or district. The platform of Teaching Channel Teams was invaluable in this process and I think would be an integral component in making this work….

The End….well, of just this piece….MUCH more to come,

Kristin

Collaborating and Learning Coast-to-Coast

3 Replies

At the end of August, I was fortunate to be selected to participate in a project through Illustrative Math, Smarter Balanced, and the Teaching Channel focusing on the fraction learning progression of students in grades 3 – 5. We are working on creating,piloting, and revising both instructional and assessment tasks that will live on the both the Illustrative and SB digital libraries. Video of this work in action will also be captured by, and live on, the Teaching Channel website. Our team is a unique mix of educators from coast to coast. Jody (IM Project Lead & Orange County Math Supervisor), Chepina (Math methods professor from KSU), Alicia (5th grade teacher from Washington state), Jennie (Alicia’s math coach) and me…5th grade teacher on the opposite side of the country! Aside from this immediate group, we have many others at both Illustrative and SB offering guidance and feedback along our way.

The first phase of this work was using a multiplication of fraction task as the center of a professional development for Orange County educators as well as the filmed lesson for the Teaching Channel. Due to the distance between us, Google immediately became our best friend! We shared documents and created our presentation in the Drive, shared thoughts and ideas through Gmail, and had many Google Hang Outs to collaborate and meet each other virtually! It was so exciting to be working together on something we all feel so passionate about…student learning around mathematics. We worked through the task together, thought about the 5 Practices in planning the lesson and designed a type of lesson study around our work.

After the PD planning was almost complete, I did the instructional task with my students, filmed the lesson, and uploaded it to Teaching Channel Teams (if you haven’t checked this resource out, I think it is an amazing opportunity for groups to collaborate around video). All of the team members viewed the lesson, made comments, and offered suggestions to improve the lesson when Alicia teaches it in the upcoming week. As an aside, the channel allows for time stamping on the video comments so you can jump right to the point of the comment, great stuff. We planned the afternoon of our PD day around this task and used work samples and video of my students to help build deeper teacher understandings around how students reason about fractions.

Planning complete, and I am off to Orange County after my half day last Friday! After a long 6 hour flight and a nearly missed connection, I arrived at the John Wayne Airport 3 hours earlier than the time my body was saying it was! That evening I got to “meet” Jody and Chepina for the first time….but not really! Google had made it feel like I already knew them! I met up with Alicia and Jennie the following day and we had such an amazing PD day. Who doesn’t love teachers who come to a professional development on a Saturday?!? We had such an interesting group of college professors, CGI reps, public and charter school teachers, and a Smarter Balanced representative. We looked at coherence of the standards along the grade levels, read the fraction progression document, did some math as learners, and reflected on that same math as educators. The math conversations were amazing and the personal ah-has in terms of fraction work, happened at every turn! I even met a new math tweep (@edtechbydarin – 5th grade math teacher) and coerced Jody to hop back on to check out Twitter (@jody_guarino)! Follow them both, they are great!

Next week, I will be heading out to Seattle to see Alicia teach the same lesson I taught and that we revised together. Jennie will be in the room coaching during the lesson and then we all film for the Teaching Channel on our collaboration and reflections on student work. I cannot wait to see how Alicia’s students do with the new and improved lesson. We changed up the number talk and adjusted the wording of the task. I will post pics and update with the task and some sample student work soon! Here is just a glimpse at some of my student work that guided our conversations about the lesson…