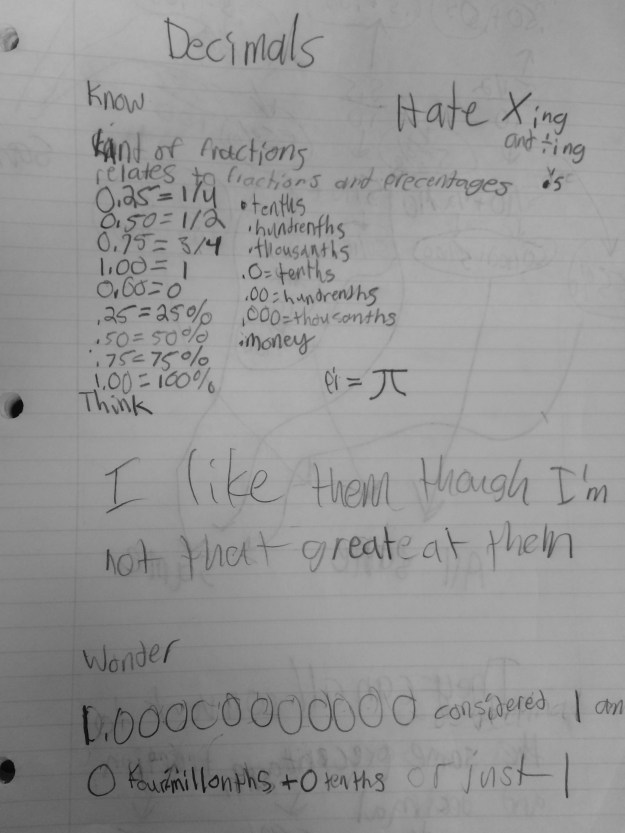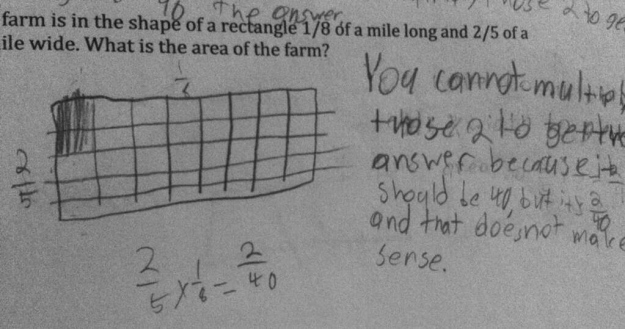Yesterday, Malke tweeted this…

…and it led to such an interesting conversation that I honestly can say, I had never really given much thought. The conversation is here if you would like to read it now, or you may want to save it until after you read my rambling thoughts. 🙂

At first read of the tweet, my initial thought was how hard it was for me to make a distinction between intuition and making sense of problems. What makes them different? The amount of time it is given? The context of the situation? The math experience behind it? My questions could go on and on. I needed time to process these thoughts and let them sit with me for a bit. I tried reading some of the links to works about intuition in learning, but until I could figure out how I was thinking about intuition and put it in the context of my classroom experiences, the readings were not making much sense to me.

Luckily, I had a lot of car-riding time yesterday to think about this and jot some thoughts down. Disclaimer: these ideas are quite scattered, do not form a cohesive string of thoughts, and you will probably be left with more questions than answers by the end, however it is really fun to think about all of the ways “Intuition” takes shape in learning.

I thought it would be good for me to start with a definition and work from there. First, I tried Webster and got this one:

eh. I didn’t like the “without any proof or evidence” piece of this because I feel that our intuitions do come with proof or evidence, they are maybe not explored or articulated yet, however I think they are there. Then I found this one that I felt I could work from a bit better:

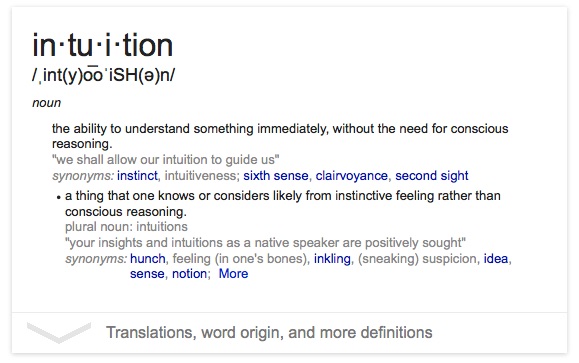This definition by no means encapsulates how I envision “intuition”, however it had some really interesting points that led me to more questions….

– Does our intuition mean we have an “understanding”?

– Where does our “conscience reasoning” come from?

– Is our intuition always what is “likely“?

– Where do I see these hunches, inklings, notions in my students’ learning of math?

– Where do I see these same things in myself as a teacher?

Up to this point, I was gaining more questions than answers, so I began thinking about these questions in terms of my students and myself as a teacher. I am a person always in need of examples, so I needed to form some “example cases” to start to clarify these thoughts.

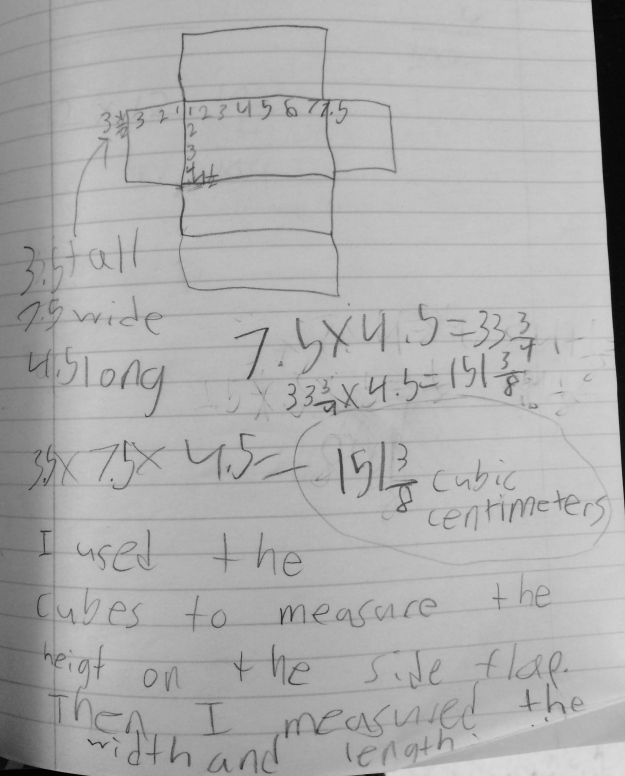
In this first example, from an Illustrative Task, the student was asked to determine if the answer to the problem could be solved using multiplication. Although the student came to the correct answer of 2/40, his intuition is telling him it still doesn’t make sense. Is this intuition based on previous experiences? Are all of our intuitions based on past experiences or non-experiences? Has he never seen an area less than 1 so it can’t make sense? The array has to be whole numbers? For me, the use of miles intuitively feels weird when I read it. Even as an adult, I hear miles and think of distance, bars, and do not like it so much with area.

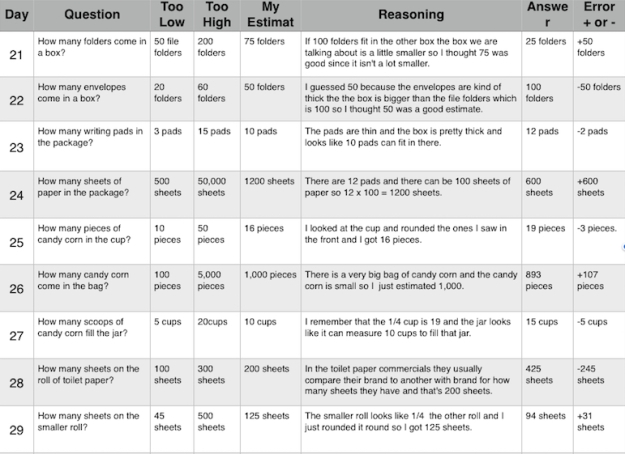
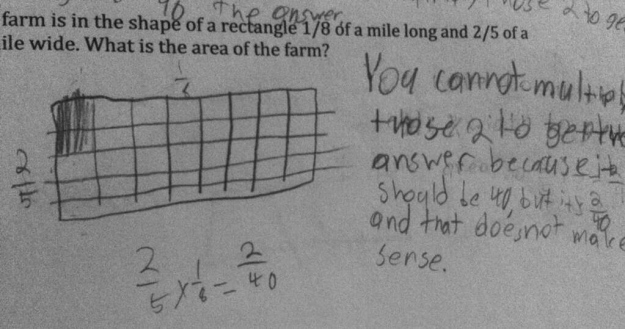In class each day we do Estimation 180. In this example, I specifically look at Day 23. I never really thought much about this, but I think it is intuitive of the student to look at the size of the item being packaged in another when thinking about capacity and volume. The student doesn’t look at the color of the paper or types of lines on it, but instead intuitively looks at the size of each part. It is something that happens so fast, that perhaps these are the quick, small moments in my classroom where students are acting intuitively.

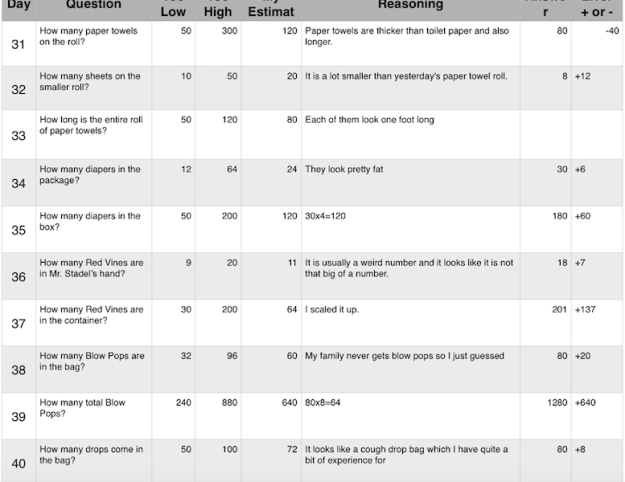
On Day 36 in the example below, a student’s reasoning is that it is “usually a weird number” and on Day 37 says “My family never gets blow pops so I guessed.” Both of these seem to stem from experience/non-experience.  The student has noticed that in previous days the packaging numbers have not been “friendly numbers” so the students is intuitively thinking it is a non-friendly number. If he/she was given this problem on the first day of the estimation questions, would their intuition have led them in a different direction? Day 37, shows a glimpse into, what I call, non-experience. This student intuitively goes to guessing because of never having them at home before, however is still only 20 off. This then leads me to question, that if a student doesn’t intuitively think of a reasonable estimate, do they then move into a more concrete strategy? To be within 20, I feel like the student used counting in the picture to some extent.

In this second grader’s work, I see such an interesting intuition in the second part of this question…

She seems to think that she cannot possibly know all of the possibilities because she is not older. She associates getting older as getting closer to knowing “all” of something. Little does she know that as you get older, you find you know less of “all” than you originally thought 🙂 Ha!

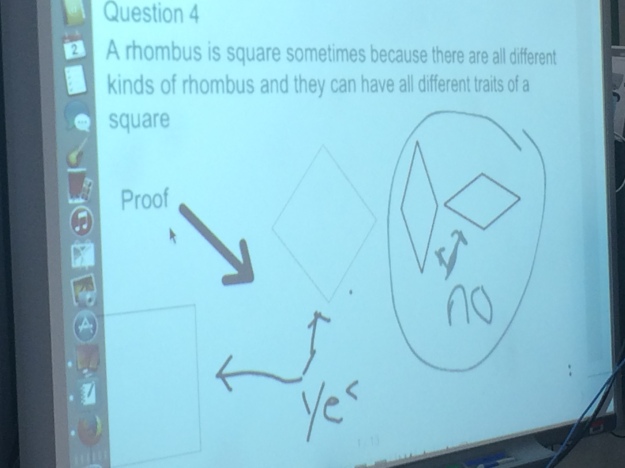
Here is where I get muddled between intuition based on experience and making sense based on prior knowledge. I asked this question to my students last year and here is one example of a student who went beyond yes or no and started to give a proof. I would love to hear others thoughts on intuition here….

This example below makes me think about how conjectures are made by students. Do conjectures stem from intuition and proofs that we can’t fully explain? The student said that when comparing two fractions, with the same numerator, she can subtract numerator from the denominator and the smaller difference is the larger fraction. Is this false intuition in dealing with the numerator and denominator as whole numbers? Thinking you can just pull them apart and operate with them as wholes?

This one may not be an example of intuition, but it is how I think about my own intuitions in learning….I try to explain them, prove them, revise them, edit them….. I would love every student paper to look like this…

In writing so far, I am really thinking that a student’s intuitions in learning math come from a “conscience reasoning” based on  prior experiences and exposure. I could truly rack my brain over this for a while, but before I do, I wanted to think about myself as a teacher also. How much do we do as teachers that is intuitive? How does that intuition change as we evolve as educators?

There are many things I do during the course of the school day that just feel like routine or habit. The hard part is deciphering where it is not just habit or routine, but instead intuition.

When writing my lesson plans, I would say I use my intuition often in the respect of anticipation.  From the minute I read the lesson, I have intuition on how I feel the lesson will “go over” with the students. I have a gut feeling if they will be interested in it, which students will be able to easily enter into the problem and which will struggle, and what strategies will emerge. All of these anticipations are based on my experiences with the students. So are these anticipations, intuitions?

As the lesson is happening, I think so much of my questioning is based on my intuition. I could not possibly have a list of questions to ask students during the course of every lesson, I have to rely on my intuition. As a student is explaining something, I am thinking to myself, “I think it would be interesting to ask _______.”  This is something that has definitely evolved based on my experience, however because of the “newness” of every day and every class, I have to rely on intuition of similar case scenarios. Something like, “I asked this question the other day and it got me nowhere, how can I ask it differently to push student thinking?” This inner dialogue during a lesson happens in an instant which makes me believe it is intuitive.

If all of this is true, then I would say that when I first started teaching, my intuitions were not as fine-tuned as they are now. Does that makes sense, can you fine-tune intuition?  Is there a point beyond thinking something is a good idea/bad idea or makes sense/doesn’t make sense that is still intuition but a more detailed, specific intuition? Intuitively, I think there is:)

A lot to think about still….Thanks to Malke, Tracy, Simon, Bridget, Kassia for a great (to be continued) conversation!

-Kristin