Category Archives: Math & Literature

Gallery Walks: Engaging Students in Other’s Ideas

One instructional strategy that I love for collaboration and public sharing of student ideas is a gallery walk. In a gallery walk, students create displays of their thinking on chart paper or white boards and then the small groups walk around the room and visit each other’s posters. And even though students create such beautiful displays of their ideas, it is always challenging for me to structure the walk in a way that actively engages them in one another’s ideas. Like any problem of practice, it takes trying out new ideas to see what works, when, and for whom.

The Lesson

Last week, it was the first 3rd grade lesson about division. We decided to launch by mathematizing Dozens of Doughnuts to set the stage for the subsequent activities. If you haven’t read the book before, it is about a bear named LouAnn who keeps baking 12 doughnuts to share with a different number of guests who arrive at her door. We read the book and did a notice and wonder, anticipating we would hear something about LouAnn sharing doughnuts and the number of doughnuts, friends, or plates, which we did.

Student Displays

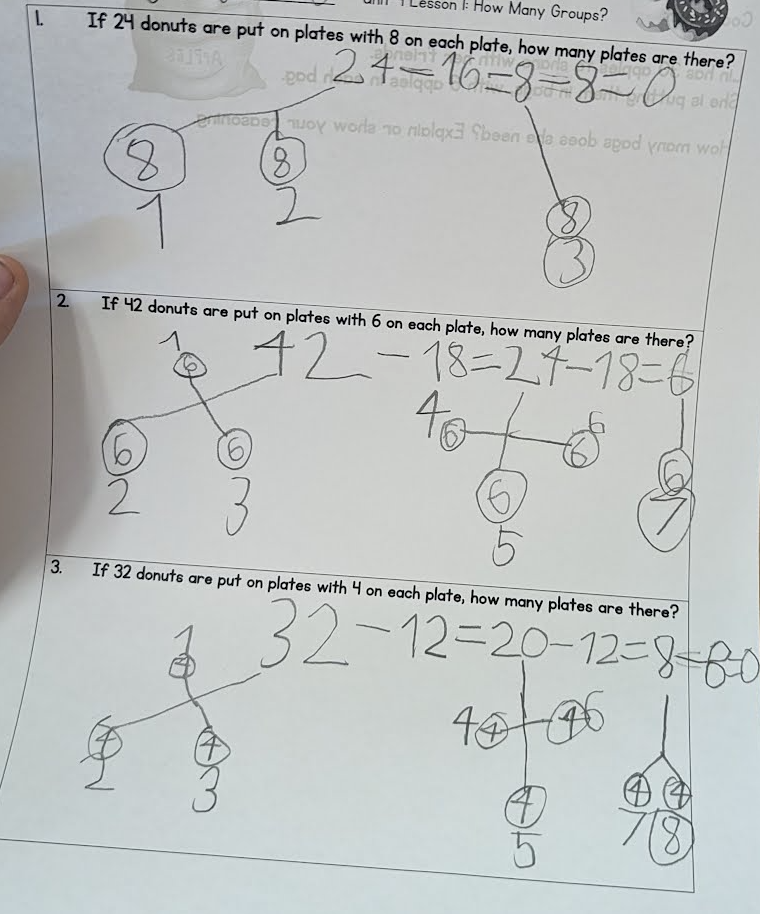
We then asked small groups to record all they ways that LouAnn shared her doughnuts. We purposefully didn’t specify the representation so they could look for different ways during the gallery walk.

As we walked around it was great to see the various ways students were representing the situations, but some small groups seemed to have settled on only one way. We had planned for them to look for similar and different ways during the gallery walk, but that can be so passive, with no opportunity for them to connect those new ideas to their work. So, instead of waiting for the gallery walk at the end, we decided to engage them mid-activity with each other’s ideas and allow time for them to use those ideas.

Taking a page from Tracy’s book, Becoming the Math Teacher You Wish You Had, we opted for a Walk-Around to cross pollinate ideas. We asked students to walk around and look for ideas they wanted to add to their poster. These could be new ideas or just a different way of representing an idea they already had.

You would have thought we gave them a chance to ‘cheat’ as they walked around with such intention to other’s posters. I wish I had captured the before and afters of all of their posters, but here are just a few where you can see the new addition of ideas.

After they finished adding to their posters, we paused to discuss the ideas they found from others – both new ideas they hadn’t thought about and ideas they had, but were represented in different ways.

Next Activity

Students then independently solved a few problems. It was great to see the variation we saw on the posters in their work. So many great representations to share and connect in future lessons!

More Ideas and Resources

Want to learn more about mathematizing? Check out Allison and Tony’s book, Mathematizing Children’s Literature.

Want to read more mathematizing blog posts? I have written about some of the books I used when coaching K–5.

Want to share your children’s book ideas for math class? Join me on IG!

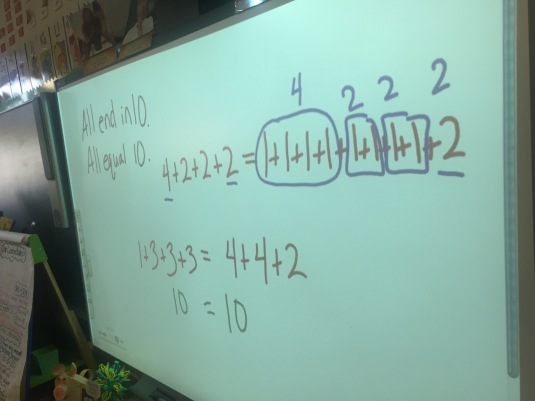
Students’ Brilli-ANT Connections in Math Class

The original lesson

Learning goal: Build arrays with physical objects and describe them in terms of multiplication.

We decided that that the diagrams and questions in activity 1 (left image) would easily come from students’ prior understandings and experiences if we launched with a context that encouraged array thinking. Once we did that, it was then about selecting which problems in activity 2 (right image) we wanted to use. We figured we could do that on the fly depending on student work and our timing.

Adaptations

New Learning Goal: Make connections between multiplication as equal groups and arrays.

We read 100 Hungry Ants to open the lesson and asked students to mathematize the situation in a notice and wonder.

The notice and wonder elicited all the ways the ants rearranged themselves which was the perfect launchpad into the activity.

Each student had a cup of 30 ‘ants’ (beans) and a sheet of graph paper if they wanted to use it. We asked them to organize the ants into 4 groups of 6 and then captured pictures of student work to share and connect. They did not disappoint! They built the same images and made the exact connections as Activity 1, however in this version, students got to decide on the arrangement based on their understandings and experiences.

We first shared a picture of discrete groups next to an array and asked how they were the same/different and where the 4 and 6 were in each. Then, we shared arrays with 4 rows of 6 and 6 rows of 4 and discussed the same questions.

At this point we could have used Activity 2 problems, but decided that since they already have 24 counted out we could save time counting out a new set by just asking them to arrange the 24 ants in a different way. We wrapped up the lesson by asking students to write multiplication equations they used today when arranging 24 ants. It was a beautiful lesson.

Takeaways

While this is one really specific example of adapting, there are some general instructional ideas that work like this makes me think more about:

When using a new curriculum, teaching the lessons as is the first year is extremely helpful in making productive adaptations. Having experienced the math goal in action and understanding what students did with the lesson activities was invaluable in adapting to better center students and their ideas.
When we plan for lessons, we not only need to understand the content, goal, and lesson flow, we also need to look for places in the lesson where students are bringing their ideas and understandings to the table, especially when we are asking them to make new connections between concepts and representations. Side note: This is one of my favorite papers on students practicing connections.
Unsurprisingly, students are so much more motivated to look for similarities and differences between their own work than a workbook example. The more we can do this, the better!
Mathematizing children’s literature is such an incredibly engaging and powerful way to elicit and discuss math ideas. While this book is overtly mathematical, students still noticed things about the storyline and illustrations that showed wonderful sense making around the context. If you want to learn more about mathematizing, Allison and Tony wrote a beautiful book about mathematical read alouds with underpinnings, examples, and structures.

-Kristin

*If you are on Twitter (I can’t call it X yet), join me and others in sharing lesson ideas and learnings like this: https://x.com/LeahBaron03/status/1710305997472797074?s=20

My One Hundred Hungry Ants Obsession

1 Reply

Lately, I have been obsessed with children’s literature across K-5. My most recent obsession is the book One Hundred Hungry Ants. I did this in Kindergarten and this in 4th grade and today I invaded a 3rd grade classroom with it!

I followed the same pattern I usually do, I read the story aloud and did a notice/wonder. These are all of the things they noticed:

IMG_2510 (1).jpg

The last one led perfectly into asking about the ways the ants rearranged themselves. I wrote the combinations they recalled from the book and asked them to chat with a neighbor about patterns they see.

IMG_2509 (1).jpg

The discussion started with the 50+50=100, 25+25=25 and 10+10=20. Another student said they had the same things but it sounded different because she saw 50 was half of 100. They moved away from that and went to divisibility by the numbers that did not show up like 3,6,7,8, and 9 and pointed out that all of the second factors were multiples of 5. At this point they were focusing primarily on the second factor until someone pointed out the increasing and decreasing pattern happening. Then we got into the doubling and halving, quadrupling and dividing by 4 and multiplying and dividing by 10 of the factors.

I asked them if that would work with any number I gave them. They were quiet so I threw a number out there for them to think about, 24. They had to move into another activity so I left them with that thought. Before I left, however, one student said yes for 24 because 2×12, 4×6,8×3. Another student said it could be sixteen 1 1/2s and then thirty-two 3/4s! Wow!

Tomorrow they are going to investigate this further to see if they can come up with a conjecture about this work! So excited!

Literature & Algebraic Reasoning

One Hundred Hungry Ants – 4th Grade

3 Replies

Next year, we are restructuring our RTI block to be a time when students are working in small groups in their classrooms. This is a really exciting change from our previous model in which students were pulled from their classroom for intervention. This change will shift our Learning Lab focus to planning small group activities, however the first, REALLY important, piece we need to focus on is how small groups work in the classroom. I think the K-1 teachers have a much better sense of how centers work within the classroom, although we still want to move from the current centers to more strategically planned small groups. So, with only a week and a half left of school, Erin and I are playing around with some ideas in the classrooms as a part of our planning! Fun!

Erin and I planned for a 4th grade class today where we were going to test out a small group scenario. We started in a way I imagine everyone could kick off the year next year, involving students in the process. We asked them what they needed in order to learn in small groups. Below are all of their great responses, most of which were accompanied by an example of something they had experienced during small group work.

IMG_2494 (2).jpg

I launched the small group task by reading One Hundred Hungry Ants aloud, pausing occasionally to ask for predictions. After the reading, I didn’t preview the task, but instead sent them off to work in their small groups. This was for two reasons: to see if the wording of the task was clear enough for students to follow independently and to see how they worked as a small group. We choose to give everyone the same task today to see how it went but we are trying different small group tasks tomorrow.

Each group had a journal, storyboard, and this task card:

Screen Shot 2016-06-06 at 7.57.14 PM.png

They worked for about half an hour and had some great conversations. I especially liked the conversation sparked by the third question because number choice is something I find so interesting. They also had to do some serious negotiating to decide which number they would do as a group since everyone had different reasons. In one group a student wanted to pick 2 because they would “get there faster,” another wanted 75 because “it could make a lot of combinations, but be less than 100 so they could still make it in time.” In another group, a student was saying he didn’t want any prime numbers because you could only do two lines with them.

This one was great because they changed the storyline from finding a picnic to getting to Dairy Queen, but when they get there they had forgotten their money so they still got no food. Different story, same ending.

This one was so interesting because, unlike the book, they used the commutative property, seeing the arrangements as different situations, which the book did not do:

This group saw a lot of doubling going on in their arrangements when they chose 50 instead of the 100 in the book:

We came back together and talked about the patterns they saw.

While the math conversation was interesting and I can definitely see some great generalizations stemming from this work, tonight I am thinking more about the questions I am left with about small group work…

Could a teacher work with primarily with one group, realistically, without continuously checking in on the others?
How can we structure the work so everyone in the group is working on the recording at the same time and can see what is being written? We saw a lot of the journal or storyboard sitting in front of one student. Not that the others weren’t contributing, but they all couldn’t see what was being written. I think dry erase boards can work well here.
What type of formative checkin can we do with each group that doesn’t add to an already growing pile of papers to be graded or give feedback?
How do we control the noise? The students were not being purposely disruptive or off-task, they were just loud and began talking louder to hear one another.
What does this look like at other grade levels?
How can we keep this interesting for students to do every day while not making it a planning nightmare?
How can we embed more student choice in the task?

More to come tomorrow when we tackle these tasks:

Screen Shot 2016-06-06 at 8.22.29 PM

100 Hungry Ants: Math and Literature

5 Replies

This week the Kindergarten and 1st grade teachers planned with Erin, the reading specialist, and I for an activity around a children’s book. This planning was a continuation of our previous meeting about mathematizing. We jumped right into our planning by sharing books everyone brought, discussing the mathematical and language arts ideas that could arise in each. I made a list of the books the teachers shared here.

We chose the book One Hundred Hungry Ants and planned the activity for a Kindergarten class. We decided the teacher would read the story and do a notice/wonder the day before the activity. We thought doing two consecutive readings may cause some students to lose focus and we would lose their attention. Based on Allison Hintz’s advice, we wanted the students to listen and enjoy the story for the first read-through. Here is an example from one classroom:

Screen Shot 2016-05-05 at 9.28.27 PM.png

So many great problem and solutions, cause and effects, illustration and mathematical ideas were noticed by the students.

The following day, the teacher revisited the things students noticed and focused the students’ attention on all of the noticings about the ants. She told the students she was going to read the story one more time but this time she wanted them to focus on what was happening with the ants throughout the story. We had decided to give each student a clipboard and blank sheet of paper to record their thoughts.

We noticed a few great things during this time..

Some students like to write a lot!

After trying to draw the first 100 ants, students came up with other clear ways to show their thinking. I love the relative size of each of the lines in these!

A lot of students had unique ways of recording with numbers. Here is one that especially jumped out at me because of the blanks:

IMG_2336 (1).jpg

Students shared their recordings at the end of the reading and it was great to hear so many students say they started the story by trying to draw all of the ants, but changed to something faster because 10o was a lot!

After sharing, we asked students, “What could have happened if they had 12 or 24 ants?” We put out manipulatives and let them go! So much great stuff!

IMG_2296 (1).jpg –>

Next time I do this activity, I would like to see them choose their own number of ants.

Just as I was telling Erin that I could see this book being used in upper elementary grades when looking at generalizations about multiplication, I found some great posts by Marilyn Burns on this book for upper elementary and middle school:

Excited to do this in a 1st grade classroom today!

MathMinds

by Kristin Gray.