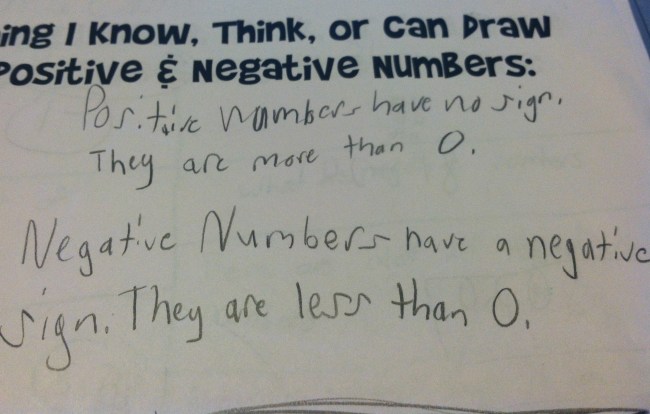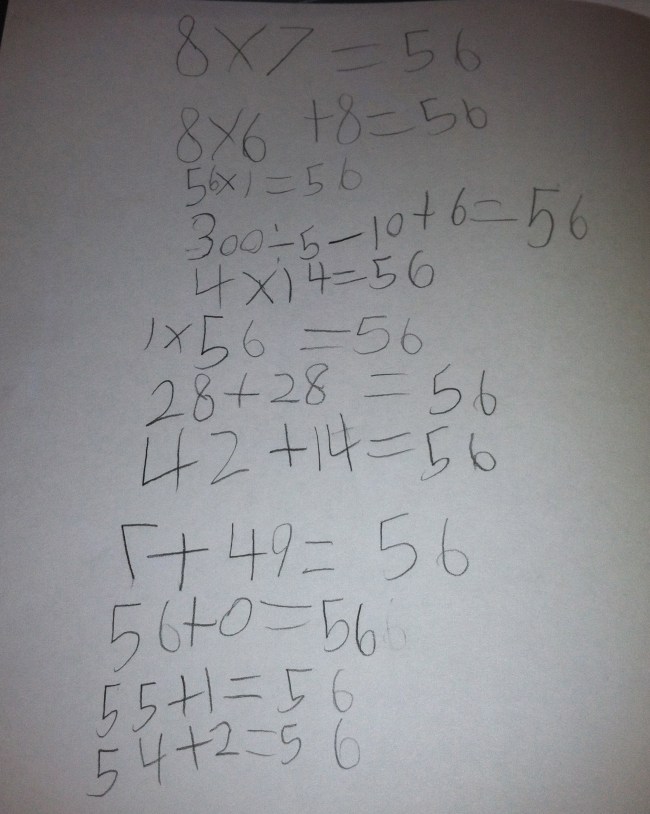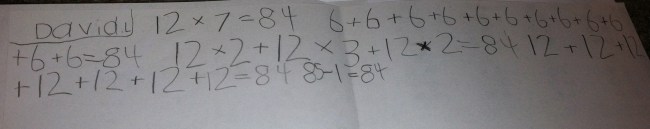It has been forever since I have blogged, and although I have been so inspired from many things I read this summer, nothing inspires me like talking to my 5th graders!
As we begin our venture into fractions, I have to first give some props to my 4th grade teachers. I have never heard so many “Yeah, fractions” and “I love fractions!” ever. I attribute this to a lot of hard work and dedication by Nancy (math specialist), the fourth grade teachers, and the Marilyn Burns’ Do the Math fraction units.
Yesterday in class, to get a feel for what my students know about fractions, we did a “Show What You Know” with problems involving writing, comparing, and adding fractions. They seemed very comfortable with writing fractions, comparing fractions using benchmarks, and finding fraction of a group.
Then we get to the problem asking students if the expression 2/3 > 2/6 is True or False. As they shared their reasonings, I heard many anticipated strategies such as “2/6 is equivalent to 1/3 so 2/3 is bigger than 1/3” and “The pieces are bigger in 2/3 and you have the same amount of each so it has to be more.”
As the conversation was coming to an end, one student raises her hand and sets my wheels spinning. She said “I know that if I just subtract the numerator from the denominator, whichever fraction has the the smallest difference is the larger fraction. But it only works when the numerators are the same.” Huh. I asked her why she thought that worked and she said she didn’t know but proclaimed it would work every time. I told her we would think through that one and revisit it soon because I needed time to think it through. Being the thoughtful student she is, I had this work from her by the end of the day:

 I was proud she gave examples and tested even and odd numbers to be sure that didn’t effect the outcome.
I was proud she gave examples and tested even and odd numbers to be sure that didn’t effect the outcome.
So my next question for myself (and anyone else who is reading and feels like offering some advice) was what to do with this…
Nancy and I sat and talked about why this works…here are some points to our discussion:
– When you subtract the numerator from denominator you could finding the fractional piece the fraction is from a whole, assuming you put it back over the denominator.
– But since the denominators are different this would not give you a piece of information that would make this “trick” valuable.
– As the denominator gets larger and the numerator stays the same the fraction gets smaller.
– So the bigger the difference between the numerator and denominator, the smaller the fraction.
– Does it work with improper fractions? Yes.
– Is it worth revisiting in class yet because some students may pick up the “trick” and not be ready for the reasoning behind why it works.
– But isn’t it really simple? 3/4, 3/5, 3/6, 3/7…and so on…the difference of the numerator and denominator is getting greater, so the fraction is getting smaller.
So in closing I have no answer of what to do with this information. I am thinking I will revisit it with the student alone because she is anxious for why this works. I may save it for the rest until I have a better grasp on where they are with their understanding of numerator/denominator relationships, but am I being too cautious? I just don’t want “tricks” to be used because they are easier for some students than the reasoning piece.
Would love any thoughts!
-Kristin