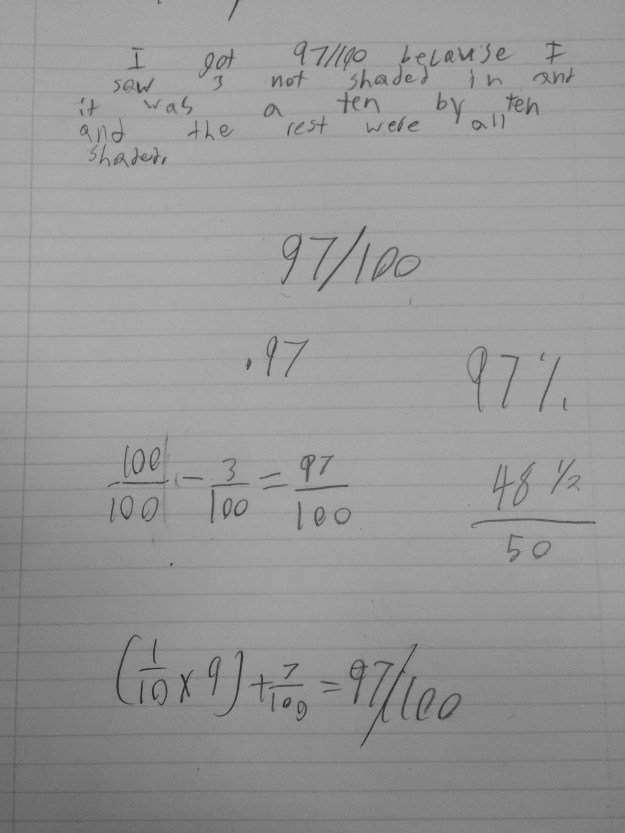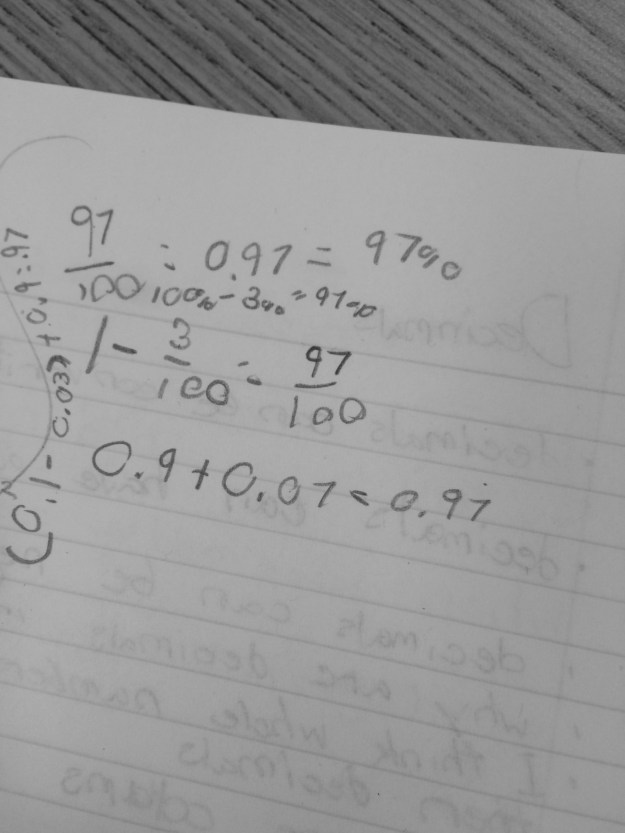It is always so interesting to me what students take away in terms of strategies for doing various tasks in math class. In this particular case, ordering and comparing decimals. We all did the same shading activities, played the same comparing games, however the way this shading is applied to student thinking is so different among the students in the class. In our assessment today I saw quite a variety in thinking that I just love.
These three are a sample of the most common strategy I saw in the work today. The students first thought about it in terms of how many tenths each decimal had. We talked about this a lot while shading in terms of full tenths, partial columns for hundredths and then parts of hundredths for thousandths so it makes sense that they would think about which decimal had the most tenths shaded first and move on from there.
This student has a comfort in fractions and changed each to a fraction in the thousandths. It is interesting that certain students like to stay in fractions, where she could have just as easily made them decimals to the thousandths.
This student explains using the hundredths grid in words. I love the use of the word blocks and 1/2 blocks. I just want to check back in on this one to see if there are connections to that 1/2 block representing 5 thousandths.
“I thought about it like whole numbers.” This is something I would be extremely worried about if she had ordered them like: .6, 0.8, .55, .125, .875 because then the decimal would have been irrelevant in their reasoning in terms of “whole numbers”. She really multiplied each by 1000, which is something I would like to revisit tomorrow with her.
I also had quite a few that compare using percents. This is a nice connection back to our fraction/percent work on the 100s grid earlier in the year.
This was a nice way to ease back in after an extended weekend of snow and ice!
-Kristin















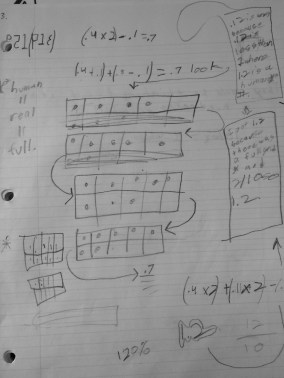



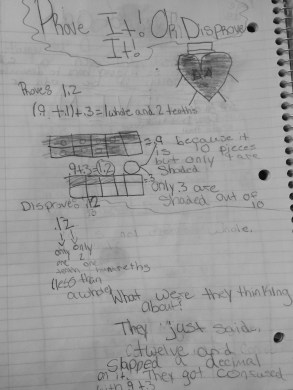
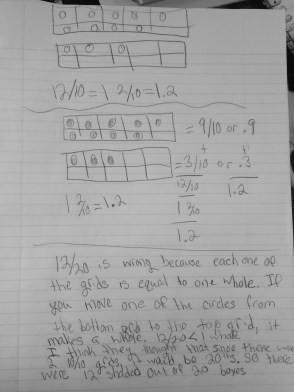


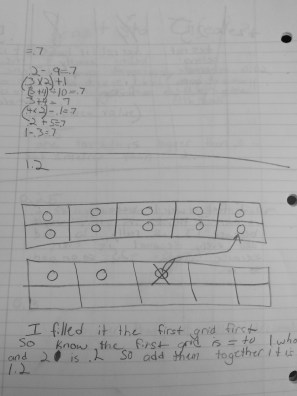
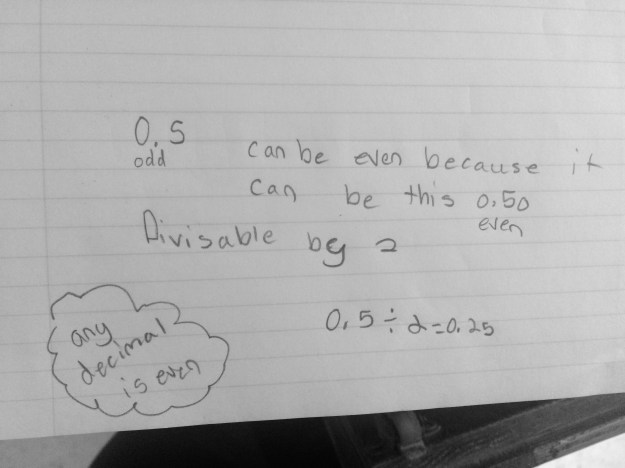
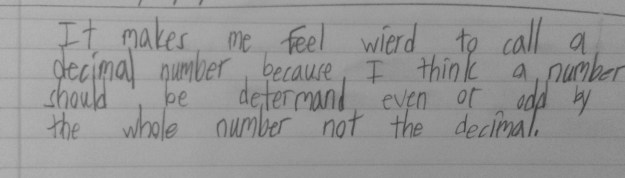
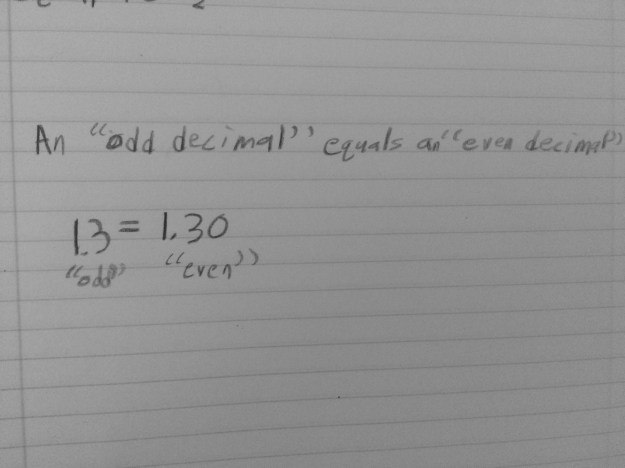
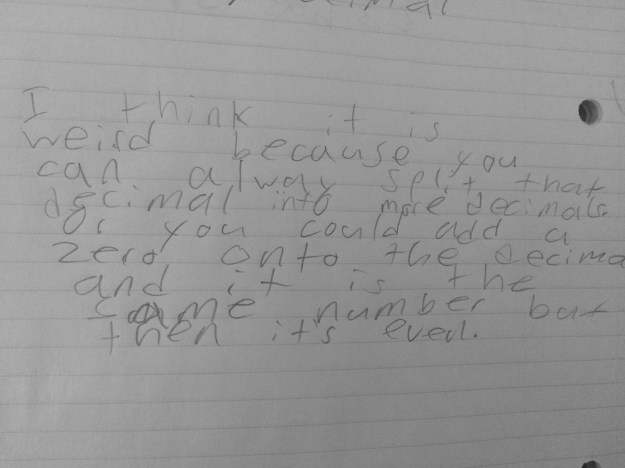
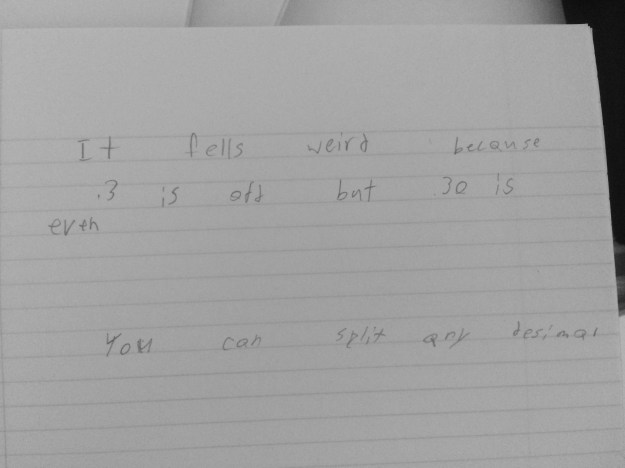













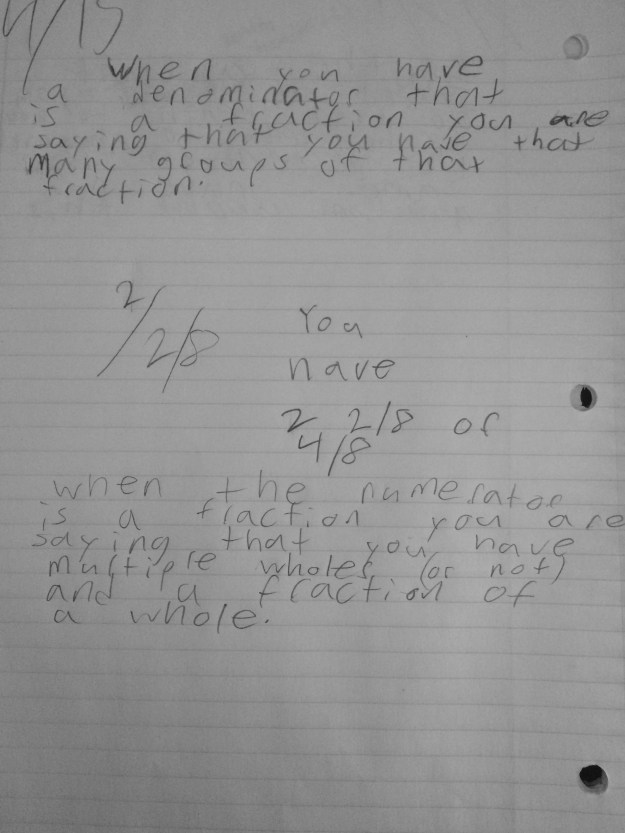


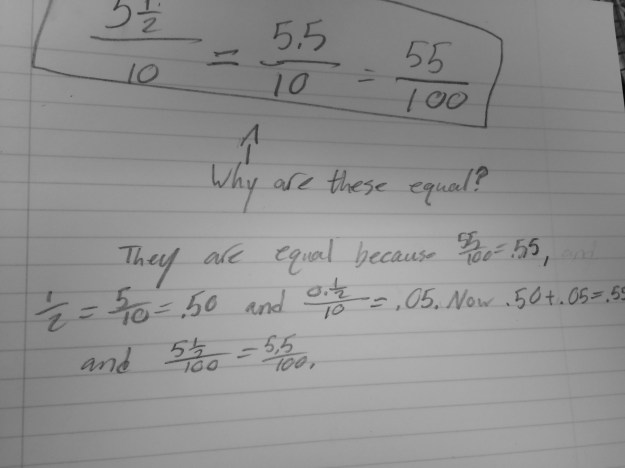
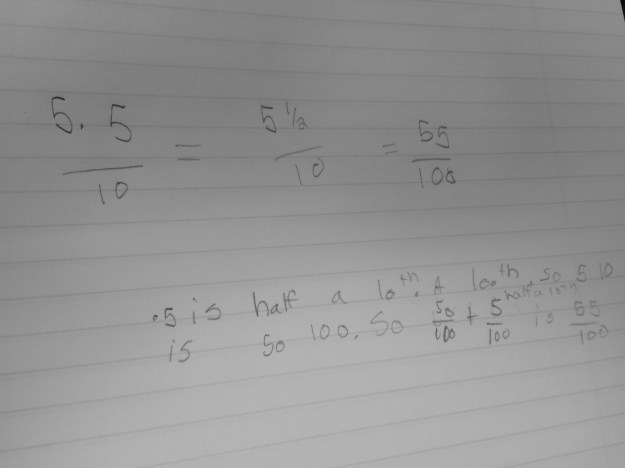



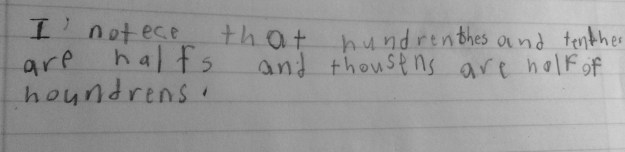

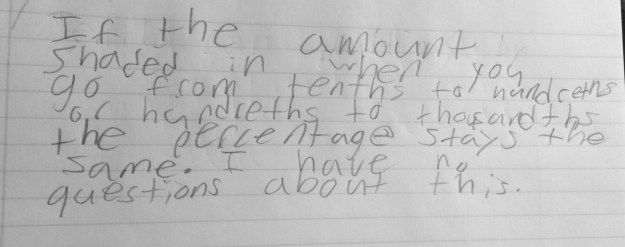
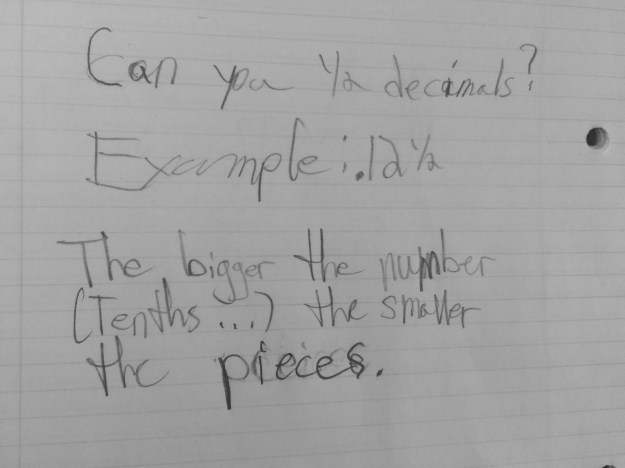

 To use the word differentiation here is an understatement. The range of thoughts in my classroom (and many many others) amaze me on a daily basis, in the most wonderful way!
To use the word differentiation here is an understatement. The range of thoughts in my classroom (and many many others) amaze me on a daily basis, in the most wonderful way!