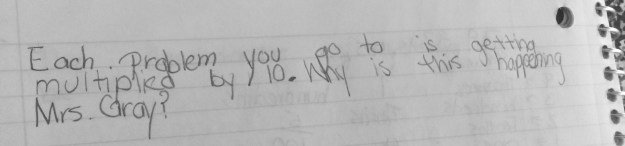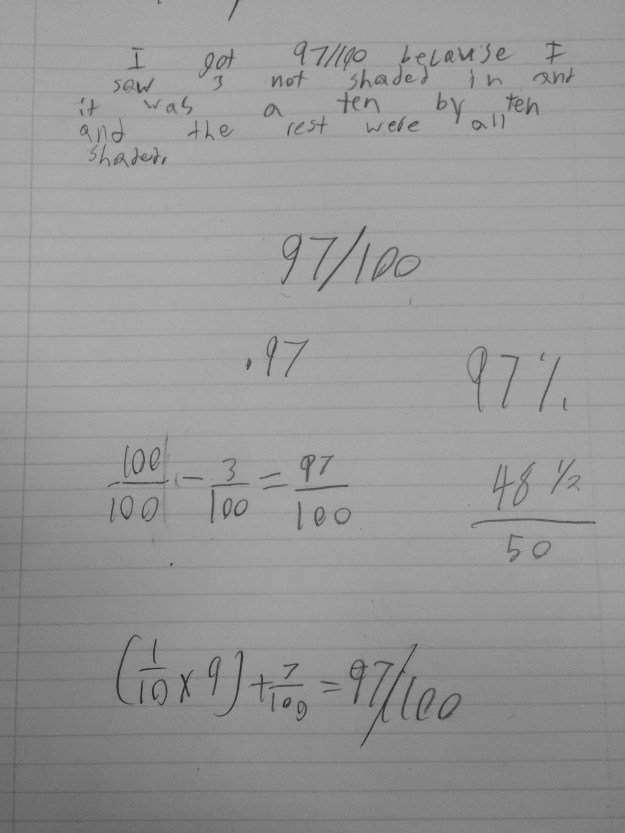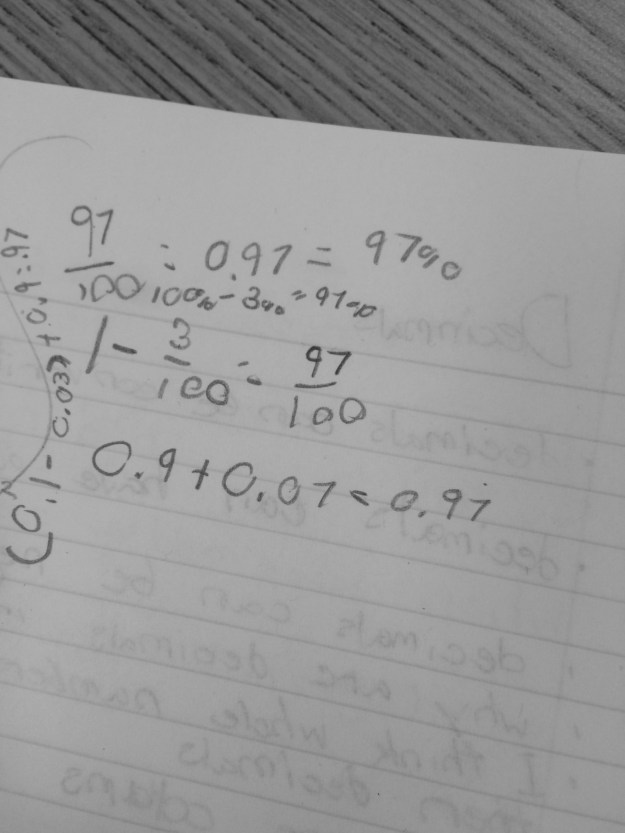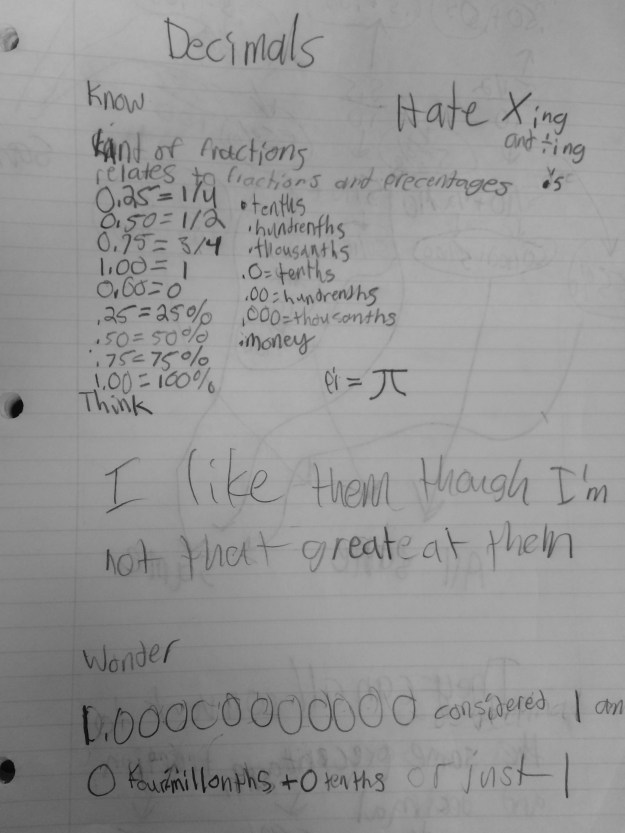Earlier this year, I had a student bring up a great conversation about odd and even numbers: https://mathmindsblog.wordpress.com/2014/11/01/things-i-have-noticed-and-wondered/
After this idea about even/odd rational numbers surfaced, I started having realizations about ideas that we, as teachers, do not ever revisit over the course of a student’s learning journey. Ideas that we could be more exact in, refine, apply constraints, or just simply play around with the idea of developing working definitions for ourselves. Properties of numbers seems to be one of those ideas for me lately.
Today I did an opening activity called, Which Doesn’t Belong and Billy’s idea resurfaced. I put the following numbers on the board and asked students which one they thought didn’t belong and why: 0.25, 3/4, 0.8. 0.5 A lot of great properties of numbers such as square, factor, multiple, even/odd, and equivalencies arose. I recorded all of their answers here, but I dug a little deeper into even/odd numbers. A student said that 0.5 doesn’t belong because it was the only one that was an odd decimal in the tenths place.
I pointed to each number one at a time, and asked for a raise of hands if they thought it was even or odd. When I pointed to 0.25 and 0.5, the overwhelming majority said odd, 3/4 they said it is neither because it is a fraction, and 0.8 was overwhelmingly even. I asked them to tell me how they determine if a number is even? I got the answers I expected, equal groups with no leftovers and looking at the last digit of a number.
I said, “So thinking about that, let’s look back at the numbers we were just discussing. Talk to your table about your thoughts now.” There were a lot of ooohs and hmmmms, and one student finally said, “Five tenths is just weird.” That statement got a lot of nods and uh huhs, but before we shared out, I wanted to get everyone’s quick initial thought on why it felt weird to call five tenths odd now since it was overwhelmingly odd at the beginning. Here are their thoughts…
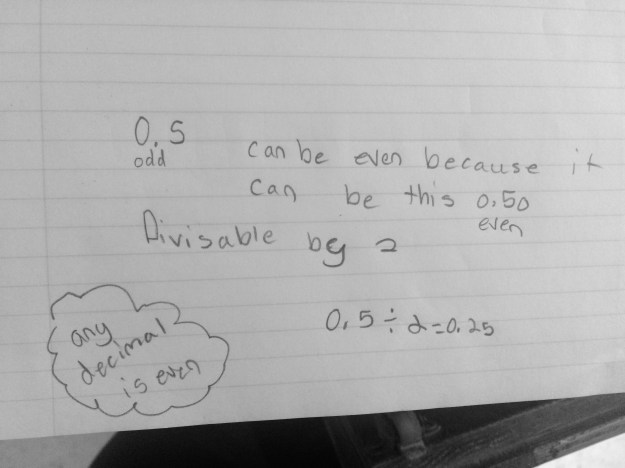
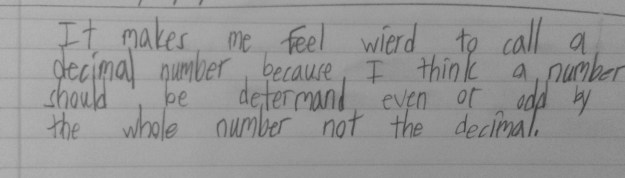
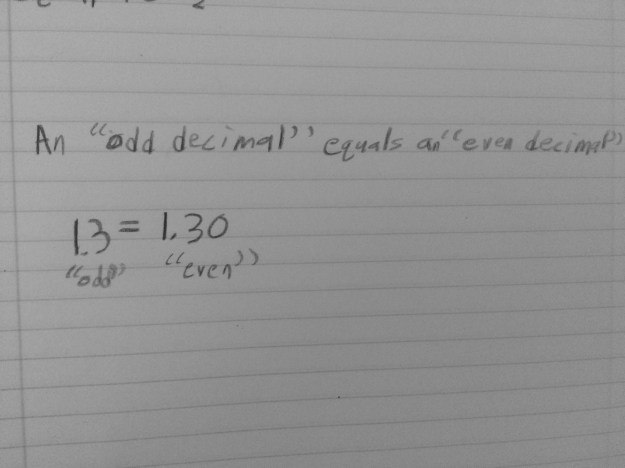
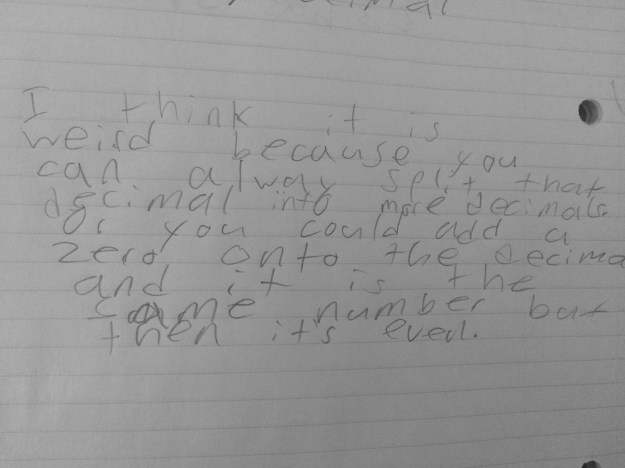
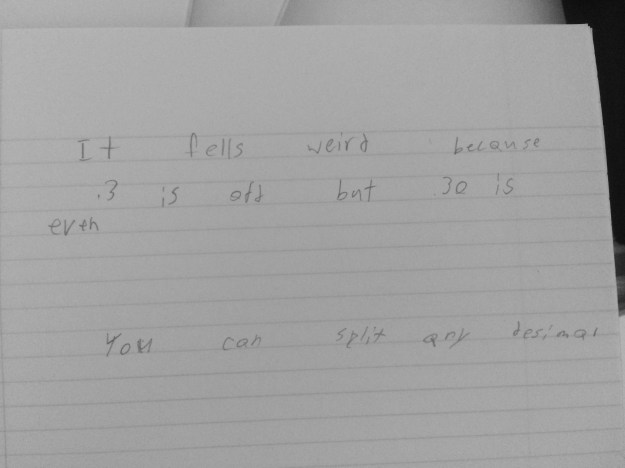
 We shared out and one student said he is going to “make a claim that all decimal numbers are even.” I loved that moment a lot! These are the working definitions that I feel are fun for students to explore. In the end, they wanted some closure and I felt they had done their due diligence, so we looked up the definition of an odd number. We talked about what an integer is and everyone felt a nice resolve to the “weirdness.”
We shared out and one student said he is going to “make a claim that all decimal numbers are even.” I loved that moment a lot! These are the working definitions that I feel are fun for students to explore. In the end, they wanted some closure and I felt they had done their due diligence, so we looked up the definition of an odd number. We talked about what an integer is and everyone felt a nice resolve to the “weirdness.”
This is something I am really interested in right now and wondering what other properties of numbers we talk about in the younger grades that don’t often explicitly resurface. Properties that apply to integers but not to rationals or even change a bit when dealing with rationals. I feel we always build on concepts as the students go through school, but do we look closely at the definitions we use and assume students don’t have more curiosities about them?
Of course I couldn’t let them leave without something to think about, so I asked them to tell me what they knew about square numbers and we listed a bunch on the board. I then put a decimal in front of each one and asked if we still called them square numbers? A few started throwing out their thoughts, but it was time to go, so more to come on that later…To Be Continued.
-Kristin












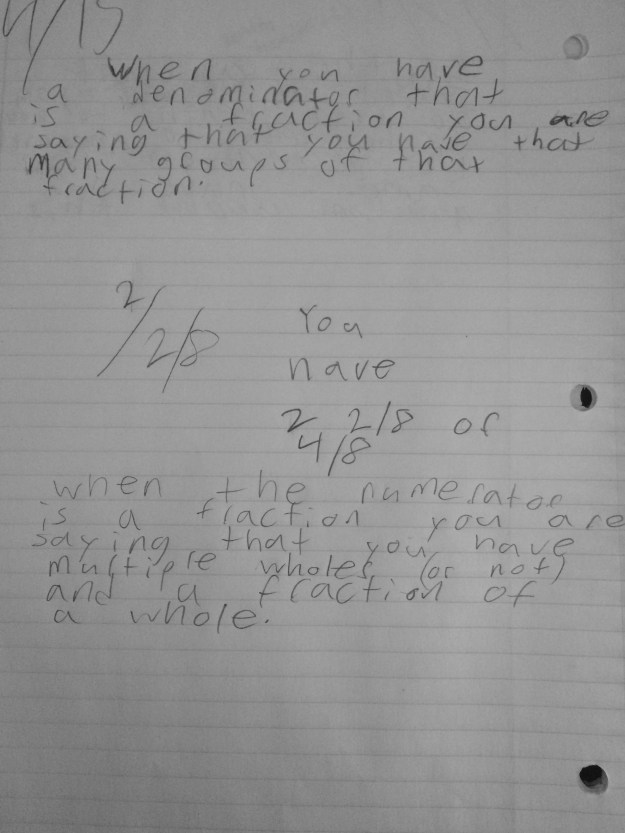


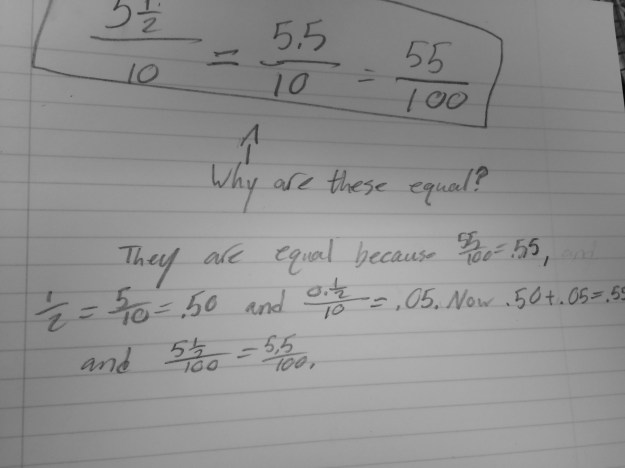
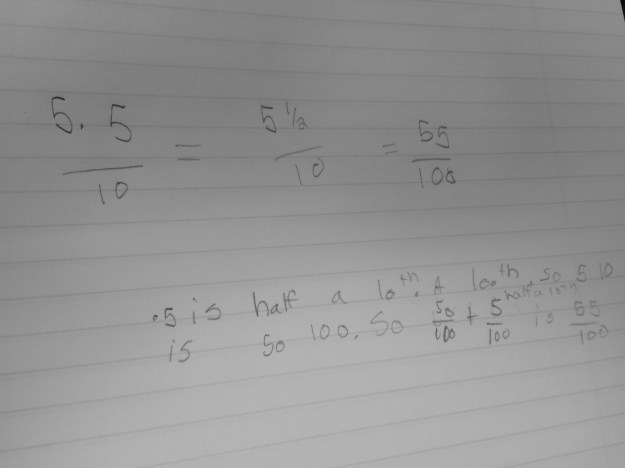



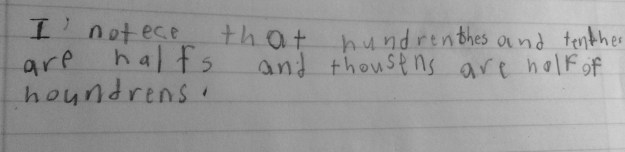

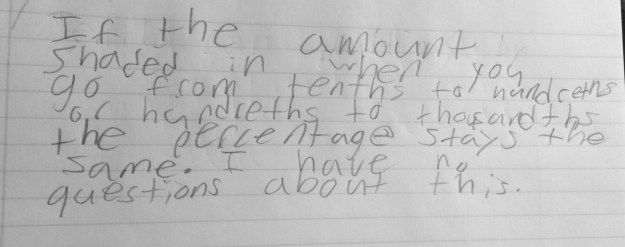
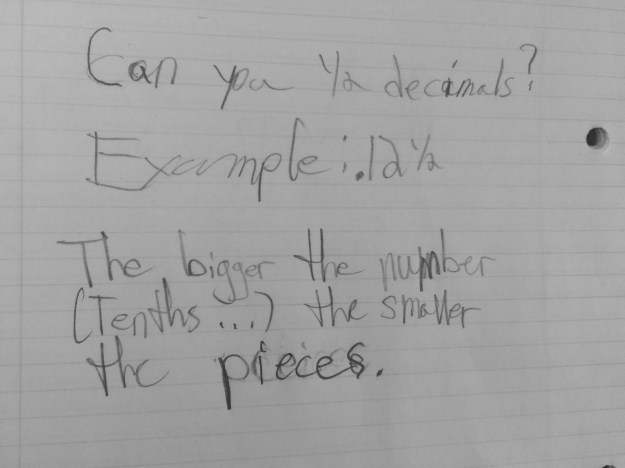

 To use the word differentiation here is an understatement. The range of thoughts in my classroom (and many many others) amaze me on a daily basis, in the most wonderful way!
To use the word differentiation here is an understatement. The range of thoughts in my classroom (and many many others) amaze me on a daily basis, in the most wonderful way!