While I am loving my new role as the school math specialist, I am definitely finding that my blogging has taken a bit of a slide. I have come to realize that my main inspirations for blogging is having a class every day in which I am thinking things through with and the student work that is the result. Working in various classrooms around the building does not offer that consistent look at student work, but I am SO excited to see so many teachers in my building using student math journals! I think they are finally starting to get used to me snapping pics of all of that great student work at the end of class!
This week, I had the chance to plan and teach with second and fifth grade teachers and do number talks in 3rd, 4th and 5th grade classrooms! Ahhhh…finally student talk and work that gets me excited to learn and inspires me to blog!:)
Second Grade:
Our second grade begins the year with Unit 3 of Investigations which centers around addition, subtraction and the number system. What the teachers and I realized, during the lesson we planned, was that, while the students did an amazing job adding and were finished fairly quickly, they all used primarily one strategy and if they did use a second one, they did see it as different.
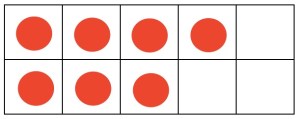
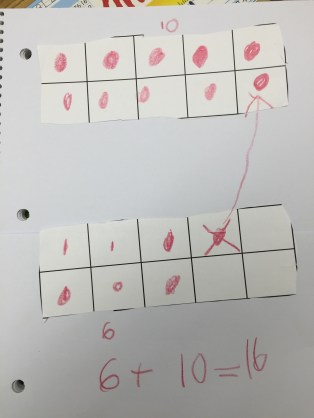
The majority of the students decomposed both numbers and combined the tens and ones like the top two strategies of this student:
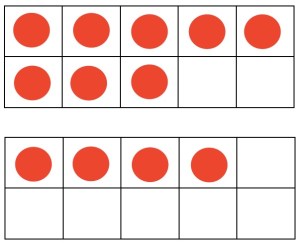
 When asked to show another way, he quickly did the third strategy. Walking around the room, the teacher and I saw many others thinking in the same way as the third strategy but intricately different.
When asked to show another way, he quickly did the third strategy. Walking around the room, the teacher and I saw many others thinking in the same way as the third strategy but intricately different.
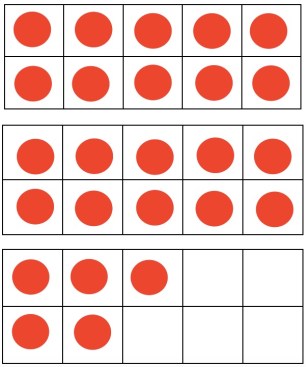
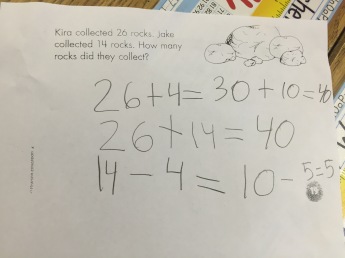 Thinking in terms of the 5 Practices, we monitored and selected a progression of papers to elicit connections between strategies, however what we found is that as students shared, the others were saying, “I did it the same way, I just broke it apart.” They didn’t see a difference in breaking both numbers or breaking one number or then how they thought about the decomposition and combining of the partial sums. We left class with that spinning in our heads….”It is wonderful they can use a strategy to add, but how do we get them to see the differences in each and think about when one may be more efficient than another?” and for me, being new to second grade math, “How important is it that they do? and Why?” The following class period, which I could not be there due to a meeting, the teacher began creating an anchor chart of strategies as students discussed them and pushed them to see the similarities and differences of each. I am still thinking through the importance of these connections and realizing I have so much to learn!!
Thinking in terms of the 5 Practices, we monitored and selected a progression of papers to elicit connections between strategies, however what we found is that as students shared, the others were saying, “I did it the same way, I just broke it apart.” They didn’t see a difference in breaking both numbers or breaking one number or then how they thought about the decomposition and combining of the partial sums. We left class with that spinning in our heads….”It is wonderful they can use a strategy to add, but how do we get them to see the differences in each and think about when one may be more efficient than another?” and for me, being new to second grade math, “How important is it that they do? and Why?” The following class period, which I could not be there due to a meeting, the teacher began creating an anchor chart of strategies as students discussed them and pushed them to see the similarities and differences of each. I am still thinking through the importance of these connections and realizing I have so much to learn!!
3rd Grade
In third grade this week, I was asked by a teacher if to come and do an addition number talk with her class. That took no thought, of course I jumped at the chance to chat math with them! I realized both before and after how much easier it was for me to plan for my 5th graders because I knew them and, due to experience, could anticipate fairly well what they would do with problems. I chose a string of addition problems that, while open to any strategies, encouraged the use of friendly numbers. I forget the exact string now, but something like 39 + 43 and 53 + 38. After being in second grade a few days before, it was interesting to see the same decomposition of both numbers to tens and ones and recombining of them. I am beginning to think that is the easiest, most instinctual way for them to do problems because they CAN do it other ways, they just jump right to that first! We did three problems together, and while the use of friendly numbers did emerge, it was definitely not the instinctual choice of the class. I left them with one problem to do “as many ways as they could in their journal (WOOHOO, they have math journals). I went back later to have them explain some of their strategies and take a look at their work.
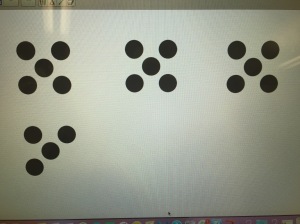
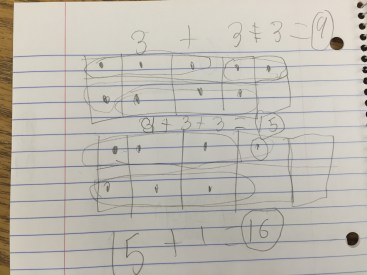
I was excited to see that while many started with tens/ones, they had a wide variety of thinking around the problem:
Of course there are always a couple that leave you thinking….
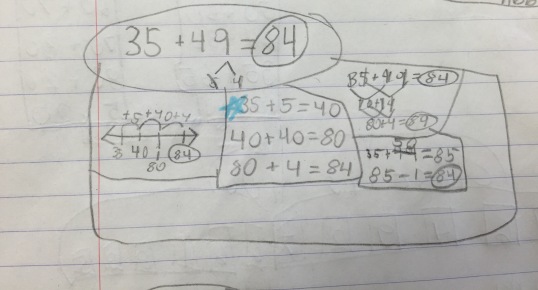
In his verbal explanation, this one said he, “Multiplied 35 times 2 because he knew that 30 and 30 made 60 and the two 5’s made 10 so that was 70. Then he added the 14 to get 84.” When he first started talking, I had no idea where he was going and was honestly prepared to hear an incorrect answer at the end. I asked him to write out his thinking and he gave me this great response:
I know we need to be aware of his use the equal sign and make that a point in future number talks, but that thinking is soo interesting. He saw he had two 35’s, one of which within the 49 and then 14 leftover once he used it in his multiplication. Great stuff!
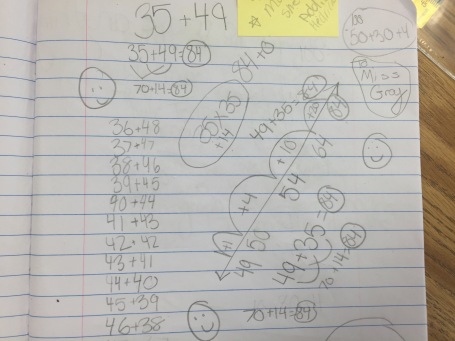
This one I need to hear more about from the student. He said he subtracted from 100 on a number line to end at 84. I asked him why he subtracted and he said he knew he needed to get from 100 to 84. I was confused but in the midst of the class, I didn’t think it was the time to go deeper with this one. I can’t tell if it is connections to things they are working on in class with 100 or something else?
I still have to blog about the 4th and 5th grade fun, but this is getting long already! I will save that for tomorrow!
~Kristin

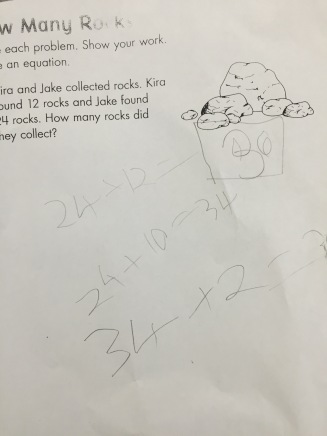












































 So, we could be looking for students to place the beginning and end (0 and 6) first and then I would be curious to see if they placed the middle number before dealing with the other numbers (line 2). Or, would students order left to right, least to greatest (line 3)? Would be interested how they think about spacing the cards in this situation, do they touch? Is there the same distance between each? What would they think about if we gave them a card with 10 on it after they finished arranging them on the line?
So, we could be looking for students to place the beginning and end (0 and 6) first and then I would be curious to see if they placed the middle number before dealing with the other numbers (line 2). Or, would students order left to right, least to greatest (line 3)? Would be interested how they think about spacing the cards in this situation, do they touch? Is there the same distance between each? What would they think about if we gave them a card with 10 on it after they finished arranging them on the line?