While I am loving my new role as the school math specialist, I am definitely finding that my blogging has taken a bit of a slide. I have come to realize that my main inspirations for blogging is having a class every day in which I am thinking things through with and the student work that is the result. Working in various classrooms around the building does not offer that consistent look at student work, but I am SO excited to see so many teachers in my building using student math journals! I think they are finally starting to get used to me snapping pics of all of that great student work at the end of class!
This week, I had the chance to plan and teach with second and fifth grade teachers and do number talks in 3rd, 4th and 5th grade classrooms! Ahhhh…finally student talk and work that gets me excited to learn and inspires me to blog!:)
Second Grade:
Our second grade begins the year with Unit 3 of Investigations which centers around addition, subtraction and the number system. What the teachers and I realized, during the lesson we planned, was that, while the students did an amazing job adding and were finished fairly quickly, they all used primarily one strategy and if they did use a second one, they did see it as different.
The majority of the students decomposed both numbers and combined the tens and ones like the top two strategies of this student:
 When asked to show another way, he quickly did the third strategy. Walking around the room, the teacher and I saw many others thinking in the same way as the third strategy but intricately different.
When asked to show another way, he quickly did the third strategy. Walking around the room, the teacher and I saw many others thinking in the same way as the third strategy but intricately different.
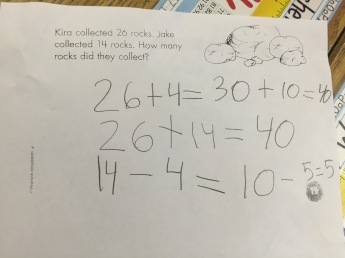 Thinking in terms of the 5 Practices, we monitored and selected a progression of papers to elicit connections between strategies, however what we found is that as students shared, the others were saying, “I did it the same way, I just broke it apart.” They didn’t see a difference in breaking both numbers or breaking one number or then how they thought about the decomposition and combining of the partial sums. We left class with that spinning in our heads….”It is wonderful they can use a strategy to add, but how do we get them to see the differences in each and think about when one may be more efficient than another?” and for me, being new to second grade math, “How important is it that they do? and Why?” The following class period, which I could not be there due to a meeting, the teacher began creating an anchor chart of strategies as students discussed them and pushed them to see the similarities and differences of each. I am still thinking through the importance of these connections and realizing I have so much to learn!!
Thinking in terms of the 5 Practices, we monitored and selected a progression of papers to elicit connections between strategies, however what we found is that as students shared, the others were saying, “I did it the same way, I just broke it apart.” They didn’t see a difference in breaking both numbers or breaking one number or then how they thought about the decomposition and combining of the partial sums. We left class with that spinning in our heads….”It is wonderful they can use a strategy to add, but how do we get them to see the differences in each and think about when one may be more efficient than another?” and for me, being new to second grade math, “How important is it that they do? and Why?” The following class period, which I could not be there due to a meeting, the teacher began creating an anchor chart of strategies as students discussed them and pushed them to see the similarities and differences of each. I am still thinking through the importance of these connections and realizing I have so much to learn!!
3rd Grade
In third grade this week, I was asked by a teacher if to come and do an addition number talk with her class. That took no thought, of course I jumped at the chance to chat math with them! I realized both before and after how much easier it was for me to plan for my 5th graders because I knew them and, due to experience, could anticipate fairly well what they would do with problems. I chose a string of addition problems that, while open to any strategies, encouraged the use of friendly numbers. I forget the exact string now, but something like 39 + 43 and 53 + 38. After being in second grade a few days before, it was interesting to see the same decomposition of both numbers to tens and ones and recombining of them. I am beginning to think that is the easiest, most instinctual way for them to do problems because they CAN do it other ways, they just jump right to that first! We did three problems together, and while the use of friendly numbers did emerge, it was definitely not the instinctual choice of the class. I left them with one problem to do “as many ways as they could in their journal (WOOHOO, they have math journals). I went back later to have them explain some of their strategies and take a look at their work.
I was excited to see that while many started with tens/ones, they had a wide variety of thinking around the problem:
Of course there are always a couple that leave you thinking….
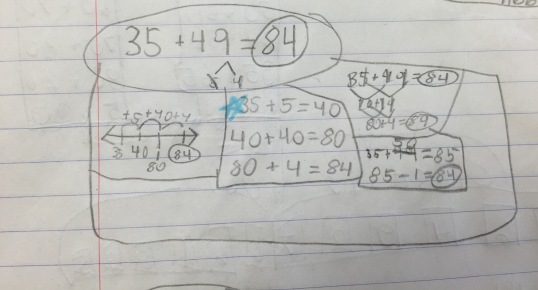
In his verbal explanation, this one said he, “Multiplied 35 times 2 because he knew that 30 and 30 made 60 and the two 5’s made 10 so that was 70. Then he added the 14 to get 84.” When he first started talking, I had no idea where he was going and was honestly prepared to hear an incorrect answer at the end. I asked him to write out his thinking and he gave me this great response:
I know we need to be aware of his use the equal sign and make that a point in future number talks, but that thinking is soo interesting. He saw he had two 35’s, one of which within the 49 and then 14 leftover once he used it in his multiplication. Great stuff!
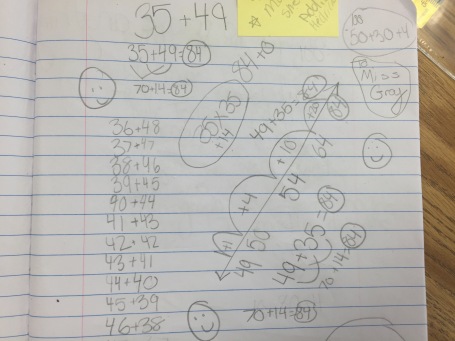
This one I need to hear more about from the student. He said he subtracted from 100 on a number line to end at 84. I asked him why he subtracted and he said he knew he needed to get from 100 to 84. I was confused but in the midst of the class, I didn’t think it was the time to go deeper with this one. I can’t tell if it is connections to things they are working on in class with 100 or something else?
I still have to blog about the 4th and 5th grade fun, but this is getting long already! I will save that for tomorrow!
~Kristin

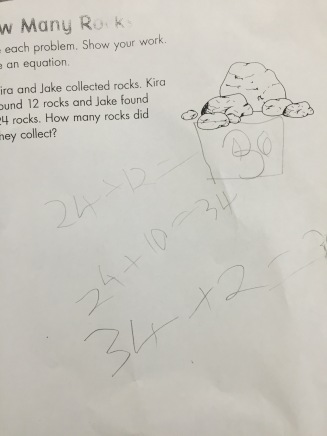


I wonder what the second grade students would say about comparing the strategies if they tried to represent them on number lines.
LikeLike
That is a great idea Nancy! It definitely looks different then and that visual may help them see the difference in what they are doing! Thanks!
LikeLike
So happy to read your blogs again, Kristin! I can relate to your new role since I, too, am a teacher who has been transplanted from classroom teacher to instructional coach position. I never take my teacher hat, off, though, so I find it fascinating to hear what kids are saying and thinking about mathematics.
It is challenging to do number talks in classrooms where you have not spent a lot of time because, as you said, when they are your own kids, you can more easily predict what they will say because you know what their background knowledge is. Love the little one who mentioned using multiplication [(2 x 35) + 14] to solve the problem. What does this tell us about his readiness for learning? How would you extend the learning for him based on his response? How do you honor this “outside the box” way of thinking without “confusing” students who aren’t there, yet? These are things that I think about as an instructional coach and as a classroom teacher.
On another note, I’ve seen the name Kristin Baughman-Gray attached to an online course offered by our local intermediate unit that focuses on observing math instruction. Just curious – is this you?
Thanks for sharing your math work! It’s so much fun learning from you! Your blog has inspired many conversations in my district.
LikeLike
Just a thought:
Often, young children learn their doubles facts early on, and then learn doubles facts +/- 1. For example, a strategy to solve 6+7 for even younger children is to say, well, I know 6+6=12, and then I added one more to find 13. [Or to say, well, I know 7+7=14, and then I subtracted one to find 13. The latter version is less likely to arise in this example, though it certainly might for 14+15.]
This strategy can be used for bigger numbers, too.
For example: 35 + 36. Or even 35 + 37.
But how do you use this strategy to solve, oh, 35 + 39?
or, & this is harder: 35 + 42?
Scaffolding in this way suggests something like, well, I know 35+35=70, and then I added seven more to find 77.
From this perspective, the 35+49 strategy can be thought of as:
35+35=70, and then I added 14 more to find 84.
[35+49 = 35+35+14 = 70+14 = 84, in symbols; it could also be illustrated by /\ decomposing …]
As a last remark [of a more personal nature]: I am always wary around the phrase “outside the box.” It is not that the student who solved this problem thought “outside the box” — rather, the student thought within a bigger box! It looks “outside” to others [& it may truly be outside their boxes for the time being] but I think it rather mystifies matters to talk about fostering “out-of-the-box thinking.” [A phenomenon I witness too often!]
P.S. @Kristin
“I know we need to be aware of his use the equal sign and make that a point in future number talks”
I was thinking the same! The end of the second grade group also shows this in its final image, where a student has written: 26+4=30+10=40. That misunderstanding/misuse has an impressive tendency to rear its head…
LikeLike
26+4=30+10=40.
This is a misuse, not a misunderstanding, unless you mean a misunderstanding of the correct use of the equals sign. The kid is trying to put into symbols what he has done, and there is real reasoning behind the statement:
“I added 4 to 26 and got 30, and then.I added the 10 and got 40”
This is two “formal” mathematical statements shoved together, 26+4=30 and then 30+10=40, so the missing bit is “and then 30”.
Kids MUST be encouraged to speak what they write, then it can be fixed.
LikeLike
Right @ misuse & misunderstanding.
LikeLike
I agree Maya, the doubles are used very frequently by students but I was really surprised to see him create the double from so far away. Like you had said, the +/- 1 or 2 seems reasonable, but to pull the 35 and leave 14 behind was so interesting. Also, at this point of second grade (only 5 weeks in) I was surprised to hear multiplication.
The equal sign misuse is so typical when students begin to write their thought processes down because it is a sting of reasoning to them and they write it just like they thought about it..in one long string of numbers and symbols:) Like Howard mentioned, going back and forth between speaking and writing is so important and something I feel Number Talks combined with journal writing hits wonderfully.
LikeLiked by 1 person
Thank you so much and it is so nice to hear that I am not alone in this coaching thing! I loved your questions and I was actually thinking the same thing about what to ask him next. I was thinking it would be interesting to hear if he would use that strategy all of the time or would certain numbers not be as “nice” to use it with, like 38 + 73? Does that lend itself to another strategy?
That is not me doing the course and I am beyond flattered to hear my work inspires conversations!!
LikeLike
I am looking at this from a “use and meaning of words” perspective.
What is a strategy?
What is a method? and
What is an algorithm?
Here is a first stab at explanation:
Strategy – breaking up numbers as a way of seeing the problem more deeply.
Method – for example, breaking up both numbers in an addition problem and adding the “bits”.
Algorithm – a set of instructions for implementing a method so that it can be applied without understanding
I feel that the word “strategy” is nowadays seriously overworked. I would like to see your observations on this..
LikeLike
That is something really interesting to think about Howard! When I read your uses and meanings, this is what I started to think…
Strategy – the thought process behind what the student is doing to see the problem.
Method – the physical process of what is being done.
Algorithm – a set of steps that combine the strategy and method.
Thoughts on that?
LikeLike
I see the initial thinking about a problem as the process of selecting a strategy, so in the example of 2 digit addition there are several possible strategies. 1. Break up the numbers, 2.use an abacus, 3. use a calculator, 4. use the “standard algorithm” and maybe more.
The actual use of the chosen strategy is then the method. I think we are on the same wavelength here.
My concerns about the use of the word “strategy” is that it is often used where “method” is meant, thus screwing up the important consideration of sequence.
Of course, and not unexpectedly, the CCSSM has been misinterpreted to the extent that “This is the Common Core way of solving arithmetical sums” is now the mantra. I am reminded yet again of the Tom Lehrer song “The New Math” from the 1960’s. If you don’t know it go to my site and search for him by name. I also have numerous posts on the misuse of language in math.
LikeLike
In second grade, we have found it helpful to discuss strategies and tools used to carry out strategy. So the strategy might be breaking numbers apart by place value and the tool could be cubes, a number line, a hundreds chart, etc. I am thinking about how “method” and also the modeling and communicating that we ask kids to do could fall into this…would it look something like this?
a) strategy: breaking numbers apart by place value
b) method: adding tens then adding ones
1. tool: number line
2. communication: words, pictures, numbers
3. model—something used to illustrate and think about mathematical ideas and concepts.
I can’t decide if this would be a part of communication? part of method?
c) algorithm: is this important for young children? or is demonstrating an understanding of the numbers and operation enough?
LikeLike
I also wonder about a strategy in which kids make an equivalent problem: 35 +49 as 34 + 50. I sometimes worry that with all the focus on breaking numbers apart by tens and ones, that students forget to really “look” at the numbers to see what would be the most efficient approach to solve a problem. (Granted that beginning of the year second graders may not be quite this flexible in their thinking yet.)
LikeLike