Category Archives: Professional Development

#ISTE2014 Reflection

2 Replies

This was my first ISTE conference so I was first completely impressed with the sheer number of attendees and organization of such a massive conference. Throw in the number of passionate educators present and it makes for an unbelievable and somewhat overwhelming experience. I wanted to jot down some of my overall impressions, takeaways, and random thoughts before summer work kicks in and I forget everything by the time school starts! I looked at the conference from two perspectives, first as a classroom teacher and then as a person responsible for the math professional development in our district.

As a teacher…

1 – I loved, loved, loved the number of educators on Twitter. The #ISTE2014 hashtag was blowing my phone up every minute of every day during the conference.  The amount of multitasking going on everywhere was amazing! I have never seen so many people engaging in technology, learning, spreading the word to others, and walking at the same time 🙂 I felt connected to the many sessions I could not attend or that closed before it even started due to capacity (that was a bit frustrating at times). It truly demonstrated the need to be a connected educator and the value of networking with colleagues around the world.

2 – I was excited to see the focus of my sessions more about the student learning than the technology in and of itself. The tweets reflected the same emotion and I loved that!

3 – I got SOO many exciting ideas to use for Open House, management, and  parent communication (http://www.kleinspiration.com/2013/05/using-augmented-reality-via-aurasma-in.html Thanks to Erin Klein:)  however I do find I struggled just a bit to relate some of my tech learnings into my math classroom. I am not one to use technology for the sake of using it and my classroom thrives on student discourse. I LOVE to hear the students talking about the math with each other and I am not a “flipping” fan. Don’t get me wrong I love to use Educreations, Minecraft, Aurasma,  Nearpod, and Padlet on the ipads, but even then, I need to improve upon using them to make the math more authentic for the students. The presenters at ISTE definitely provided the inspiration and wealth of tools I can look into when doing my planning. Teachers are doing AMAZING work out there and it was so inspiring to see that during the Sessions.

4 – As a presenter as well, I loved all of the support in the room! From sound to video, to ISTE representatives, to Apple Distinguished Educators, there were tons of people on hand to make sure it was perfect! Well Done!

5 – The Expo was packed with exhibitors. I was excited to chat with @Schoology as a new LMS for my classroom and for my K-2 teachers, I found a great new product from a company called Osmo (https://www.facebook.com/PlayOsmo?ref=br_tf). Check them out! There were many more interesting ones I chatted with,  however after being in heels all day, my feet could not make the trek around to everyone 🙂 One thing I find intriguing at every conference I attend, is I always have to ask myself, do the vendors here convey the mission/vision of the conference organization itself. For example, at NCTM, I find vendors selling programs/products that, in my humble opinion, do not support the Mathematical Practices and vision of what best practice is in the classroom. In the case of ISTE, I saw a vendor with bubble sheet reading software that worked with any document camera (and of course his example was a math sheet…ugh) . Don’t get me wrong, it was amazing how fast it could read the bubbles and plop a grade into their accompanying grading system, but is that truly what we see as a vendor who should be at an educational conference? Just like at NCTM, do we want a timed test program to be supported by an organization who’s vision is to “…ensure equitable mathematics learning of the highest quality for all students…” I always just find that interesting.

6 – I had the opportunity to participate in a live #satchat. It was such an amazing opportunity to meet face to face with all of the avatars I chat with on many Saturday mornings! Definitely a highlight!!

From a professional development standpoint….

I was absolutely blown away by the organization and setup of ISTE. There was something for everyone and more! There were workshops, IGNITE sessions, lecture sessions (with some recorded so attendees could watch from the tv in the hallway in case of overflow), Playgrounds where teachers were encouraged to play with the technology and experience what it was like to be a student, and Poster Sessions which I can best describe as an overwhelmingly exciting “science fair” with tables set up and manned by teachers and students describing the exciting work being done in classrooms around the world!

The format of each element was genius and definitely something I want to bring back and use in my school/district. I think starting our opening district meeting with and IGNITE session showcasing district happenings would be an amazing, invigorating way to launch the school year. I also love the feel of a Playground in which teachers just play with the math and can choose the topic that best fits their needs. A district/school hashtag where we can easily share resources and ask questions would be amazing…now to just get everyone on Twitter:).

Overall it was a great experience and I still continue to learn on the #ISTE2014 hashtag! It is full of passionate educators focusing on learning, not simply the technology. Thank you all for a wonderful conference! Looking forward to Philly 2015!

To PD or Not PD..That Is the Question

3 Replies

The past two years as Math Specialist, I was in a position in which I was continually planning and attending Professional Development on a regular basis. I am a learner, so I frequently got frustrated and a bit upset when teachers complained about attending the PD. I would hear such things as, “I need time to grade my papers” or “Sub plans are such a pain to write.” How could they not love these learning experiences as much as me?

Fast forward to this year, I am back into the classroom, and I completely feel their frustrations. I have papers that need to be graded, I despise sub plans, and most importantly, l have lesson plans that I need time to think about & dig deeper into. Time, as always, is a high commodity. So, as I was in my classroom Thursday evening, writing sub plans (or more accurately procrastinating by finding anything in my classroom that needed to be done BESIDES writing the plans) I found myself thinking that it would be so much easier to not attend the PD (it was by choice I was going) and just stay in the classroom on Friday. No sub plans, and I would have my planning time to get the paper grading and lesson planning done.

This was it, this is the point where teachers (me included) need to step out of their immediate surroundings, look at the bigger picture, and ask themselves the following questions….

1. How can I continue to improve student learning in my classroom if I don’t dig deeper into my content area(s)?

2. How can I grow as an educator alone?

3. How can reflecting on my own teaching with others improve my classroom experiences?

4. How can what I know about teaching help others in my network?

5. There is always SO much more to learn. Not a question, I know, but it is my driving force as an educator.

And….How great is it to have breakfast and lunch made for me and I can use the bathroom anytime I want 🙂

Needless to say, I always try to attend professional development when offered the opportunity and after leaving my PD on Friday I just found myself smiling. I love talking to others with the same passion for mathematics and teaching as myself. I learn so much and just flat out have fun while talking about impactful issues in education. We all want what is best for our students and staff and work together to make great things happen.

Don’t get me wrong, I am picky when choosing my PD. It must be relevant. I have sat in a mandatory PD or two (hundred) that have not been what I needed, but I try to find at least one thing I can take away. Even through the bad experiences, I grow. If a presenter is not engaging, I think about what I can do when I facilitate to be engaging. If the content is confusing, I think about how I can clarify things when I facilitate a professional development. I don’t let one bad experience kill all professional development opportunities for me. They are independent variables, like a die. One roll does not impact the next. One bad professional development does not impact the next one.

In the end, I owe it to my students to go. If I am learning more, they will be learning more.

Happy Saturday,

Kristin

Why We Need Two Teachers in Every Classroom…

2 Replies

This job takes two brains to handle the thoughts of these students.

In class on Friday, one student made the comment that he didn’t really like adding fractions on the clock because it could only be used for certain fractions.  When I asked him to expand on that, he explained he could only do halves, 3rd, 4ths, 6ths, 12ths and 60ths easily and what if he wanted to do other fractions like 1/8 or 1/24?  He said he couldn’t do that without breaking the minutes up.  I am excited at this comment especially because this student is one whose parents have taken him to Kumon math for years for “extra help” and he is most comfortable memorizing procedures over thinking about the math. He thinks changing to “common denominators by multiplying the numerator and denominator by the same number” is faster and easier than this clock.

Upon reflection, I think it is interesting that he stayed with fractions of the fractions we were working…why not pull out 1/9 or 1/11? But my first train of thought in the moment was changing the whole. I wanted to see if he could put the clock in terms of a whole day, 24 hours, 2 rotations around the clock being the whole instead of one. That way 8ths and 24ths would be more apparent.

So I asked him if he could think of a way we could change the clock to do 1/8 or 1/24 without breaking up minutes? His first reaction was no, so I said “That is interesting because there are 24 hours in a day, so I feel like this should work.” Possibly leading him too much but at that point I could see the glazed look in some of the students eyes and I felt like I was losing the class’ attention. I told him that during math workshop that day he could chat with me about it or he could take that thought and work with some more for Monday.  He said he wanted to think about it over the weekend…I think mainly because he didn’t want to miss the Math Workshop activities, so we will see what he has for me tomorrow.

After school, I am recapping this lesson for Nancy and saying how difficult I thought it would be for them to grasp two rotations of the clock as the whole for the 24 hours that would allow for 8ths and 24ths more easily.  After listening to me ramble for about 5 minutes about this idea, she casually says, “What about military time?” UMMMmmm…DUH. Where was she during that class period??  This job really does take two brains.

So needless to say, I have amended my lesson for tomorrow. I am handing them this military clock and letting them talk about what fractions we can work with easily that are the same as our first clock and which one’s are different. Design addition equations we can solve with this clock that we couldn’t do on the other clock without breaking minutes.

Image

Don’t get me wrong, I still want to get to changing the whole on our original clock, but I think after working with this clock, it may be more accessible for more of the students. I will post later to update on this lesson to show how it went…but good or bad, the questions and thinking that led to this lesson are so worth it!

-Kristin

Meaningful Math Conversations…

2 Replies

I am a true believer that content coaching is a necessity in the improvement and sustainability of math instruction, however we all know that finding time to even use the restroom during the course of the school day is close to impossible! So how do we find time for these important conversations to happen and more importantly, we need to be fortunate enough to have a position in our school that does just that, coach.

Last week, my class was working on finding fraction/percent equivalents using a 10 x 10 grid.  They did great with the fourths and eighths, but then we hit 1/3!  As I walked around and talked to the students, I saw a range of strategies: shading one out of every 3 squares, shading one out of every 3 rows, then squares, and some just knew that three 33’s was as close as they could get with whole numbers and had just shaded 33. No matter which strategy they chose, the “leftover box” was leaving many perplexed.

After quite a bit of struggling with what to do with this leftover box and some happy to just settle at 1/3 = 33%, Nancy (our math specialist, former 3rd grade teacher, and partner in crime with all things math) came into the room.  She helped me by chatting with a group about their thoughts on what do with this 100th box. Class, unfortunately, had to wrap up to go to lunch, and I wasn’t comfortable that some students had had sufficient time to think about it, so I left the class with that leftover box as food for thought that night.

Over lunch, Nancy and I were talking about what she had heard from the students and she made the statement, “It is amazing how they don’t make connections to all of the sharing brownie work we did in 3rd grade when trying to count off by 3’s in the grid..” For those who use Investigations, you will  know the exact lessons to which she is referencing, for those who don’t you can probably infer the context 🙂 We discussed the difference of the contexts for students, the array work they do in 4th grade and then tried to figure how to make that connection for my afternoon class. Tall job for the 15 minutes left of lunch, AKA speed eating.

I typically start my class with some type of number talk, so we sketched out a number talk that focused on the brownie problems of years past. Lunch ended and when the class came in the classroom, they headed to the carpet for a number talk.

I did the following sequence of problems, sharing strategies as we went:

How can four people share one brownie?

How can four people share 6 brownies?

How can four people share a pan of 21 brownies?

They did an amazing job and were very confident in their strategies and I definitely put them into a “fraction state of mind.” We then went into finding our percentages and even the strategies for finding the percents equivalent to fourths and eighths seemed smoother and then when we hit 1/3 and that leftover box was much less mysterious.  There were still a few who struggled but I definitely could see more perseverance and entry points at problem solving. They seemed to make a connection to the brownie problems at the beginning of the lesson.

This entire rambling of my thoughts really boils down to one thought….Improving instruction is about finding time to have those meaningful math conversations. Had I not had that conversation with Nancy and changed my number talk for the second group, the lesson was going to have the same fate as the first.  That conversation helped me make math connections that I could then make my students. Would I have loved to have more time to think out this lesson and retry it the next day, of course, but did Nancy and I improve it…absolutely!

~Kristin

NCSM-Jo Boaler-Promoting Equity Through Teaching For A Growth Mindset

2 Replies

1As you can see from the picture, it was a packed house! After waiting in line for fifteen minutes, I was so lucky (and excited) to get a seat to hear Jo Boaler speak, even if my seat was in the next to last row.

Jo opened the presentation with Dweck’s research on mindsets. “In the fixed mindset, people believe that their talents and abilities are fixed traits. They have a certain amount and that’s that; nothing can be done to change it. In the growth mindset, people believe that their talents and abilities can be developed through passion, education, and persistence.”

Jo states that the fixed mindset contributes to one of the biggest myths in mathematics: being good at math is a gift. She referenced her book, The Elephant in the Classroom (added it to my reading list) and showed the audience various television/movie clips that continue to perpetuate this mathematical myth.

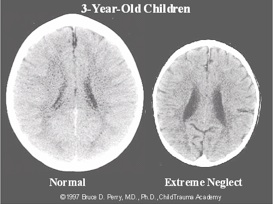
Jo then moved from Hollywood to the science behind the learning.  She briefly discussed brain plasticity,  the capacity of the brain to change and rewire itself over the course of one’s lifetime. When learning happens, synapses fire and create connections.  These synapses are like footprints in the sand, that if not used, wash away. To illustrate this plasticity, Jo showed the variation in two child brain scans, one child from a loving home and the other living in extreme neglect.  At this point, the neuroscience has me completely transfixed, so interesting.

2

Jo went on to discuss the London “Black Cab” Drivers. To become a Black Cab driver, one must pass a test called “The Knowledge” consisting of 25,000 streets and 20,000 landmarks. I had to Google it to find the image because I thought DC was bad…

3

Brain scans have shown that Black Cab drivers have a larger hippocampus after studying for and passing this test, demonstrating neuroplasticity, the brain changing/rewiring as new things are learned.

She shared a letter from a high school math department against using algebra II as a graduation requirement. The letter, in so many words, implied that certain students can’t learn, whether it be because they are minorities or due to lack of maturity, and would not be able to pass this requirement.  The reasoning in the letter goes against brain research that shows that every child can excel in math. I am so impressed with Jo’s use of research to dispute the comments we hear all too often, even at the elementary level.  Research shows that every learning experience changes one’s “ability,” yet we used fixed ability language often, “high kids and “low kids.”

Jo read a quote by Laurent Schwartz, “What is important is to deeply understand things and their relations to each other.  This is where intelligence lies.  The fact of being quick or slow isn’t really relevant.  Naturally, it’s helpful to be quick, like it is to have a good memory.  But it’s neither necessary nor sufficient for intellectual success.” I think that needs to be a poster every classroom wall!

So how does mindset impact how students view themselves? Jo shared 7th grade data in which students with a growth mindset outperformed fixed mindset students. Growth mindset students demonstrated more persistence in challenging situations and the gender gaps were eliminated in SAT levels.

Jo posed the question to the audience, “What do you think encourages a fixed mindset in a student?”  As we discussed our thoughts, I checked out Twitter only to find there were a few folks tweeting about this particular session, so we shared our ideas:

4
Jo suggested that student grouping, assessment & grading, and the math tasks we use in our classroom all contribute to creating a fixed mindset in a student. She presented this block pattern to the audience:

5

Typically, teachers would ask how many blocks will be in a certain figure number, leading to an input/output table response. Jo suggested asking students, “What you see happening?”” How do you see it growing?”
She showed video of a group of students working together for over an hour, sharing how each saw the pattern growing/changing.  They were engaged, following different pathways through the problem, creating arguments, and persevering. Ah, the Math Practices again…I do love seeing them in action! She suggests that when tasks are open and engaging, a growth mindset is developed.

I have to confess, I was reading some tweets about Jo’s session from other #NCSM13 participants at this point. I heard Jo mention Gauss and Cathy Humphries, so I jotted them down to check out later.

My attention was quickly drawn back in when Jo said, “Grades are not that important.” Thank you and thank you! She stated that diagnostic feedback of classroom observations leads to higher achievement in students. Then, the popular topic of timed tests arose.  According to neuroscience, math should never be associated with speed.  She shared numerous honest, yet sad, student reflections regarding timed tests. A 4th grader said he/she feels,”nervous because I am scared I will not finish or make a mistake.” A 2nd grader said he/she feels “that I am not good at math.”

Mistakes are good, mistakes grow synapses and yet students are pressured to NOT make them. Why? Jo stated that students have been brought up in a performance, not learning, culture. Jo ended with the message that teachers and students should be encouraged to have a growth mindset and how we teach will impact each student’s mindset. Awesome session!
Jo Boaler: http://www.joboaler.com

Marilyn Burns – NCSM presentation

Leave a reply

When Dan Meyer tweeted for volunteers to recap sessions at NCTM, I thought it was such a great idea! What a wonderful opportunity for educators to learn from wherever they are!

When I sat down to write my first recap, it was harder than i thought. Taking my crazy notes and organizing them into a digestible format for readers was difficult, but here it is…

[Marilyn Burns] NCSM: Helping Teachers Connect Assessment of Numerical Proficiency and Classroom Instruction
Image

Marilyn opened the session with a brief description of her Math Reasoning Inventory (MRI), “MRI is an online formative assessment tool designed to make teachers’ classroom instruction more effective. The MRI questions focus on number and operations and are based on content from the Common Core State Standards for Mathematics prior to sixth grade. They are questions that we expect…and hope…all middle school students to answer successfully.”  From there, she outlined four uses of the MRI (or any MRI-type student interviews) to help teachers connect assessment to instruction: embed MRI clips into classroom instruction, use the interview questions to develop properties of operations, analyze student errors in reasoning and use interview answers to inform classroom instruction.

Marilyn described a number talk she had recently done with a group of 4th graders.  She posted 99 + 17 on the screen and asked audience members to share strategies with people seated around them.  After a few moments, the audience reconvened and Marilyn shared example reasonings from her 4th graders.
Some examples were:

She explained that during her number talk with the 4th grade students, she recorded the students’ reasonings on the board with their name beside it and offered other students the opportunity to agree, disagree, or share another way of solving the problem.  After the students had given all of their solutions, she showed them MRI video clips of 5th graders solving the same problem. After each clip, Marilyn had the 4th graders revisit their responses and relate the video solution to the recorded class solutions. I thought this was an amazing way for students to make connections between strategies, when not “worded” the same way.  For example if someone had added 100 + 20 and then taken away 4 to arrive at 116, it is a compensation strategy like example 1 above, however may look different numerically. This difference in appearance could lead to mathematically rich conversations in determining relationships of strategies among the students.

The next problem Marilyn posed to the audience was 15 x 12. She asked audience members to share strategies with the people seated around them.  After a few moments, the audience reconvened and Marilyn shared example reasonings of the problem on the board.
Some examples were:

We watched videos of students solving the problem and discussed the distributive property of multiplication over addition. Typically students decompose numbers by tens and ones, however when we do something like 12 x 12 to start, we are not using that same reasoning. Marilyn went on to discuss that we tend to look at the distributive property as multiplication over addition, however it could be multiplication over subtraction as well.  These discussions, when used in the classroom, help develop the students understandings of the property of operations and promote the standards of mathematical practice.  Marilyn showed video of a student solving 15 x 12 using the standard algorithm. I have to stop for just one second to say that I cringed a bit at the use of the term “standard algorithm.”  While I understand most teachers use it to identify “traditional” multiplication, I would argue that any algorithm could be standard if worked efficiently by a student. Ok, back to the presentation. The student arrived at the correct answer, however when explaining her process, it is clear she lacked numerical reasoning when computing mentally.  Marilyn further explains that the algorithm is not a concern on an individual problem, however IS a problem when it is the student’s only strategy.  She made a connection between properties of operations with whole numbers and decimals by posing the question, 1.5 x 20. We watched student videos and discussed the use of the distributive property in this problem vs the use of the associative property.

Marilyn revisited the problem 15 x 12, however this time asked the audience to guess the top two incorrect responses students gave for this question. The general consensus of the audience was 110 (10 x 10 + 5 x 2).  The second most common was 30, we were all a bit curious where that came from, including Marilyn.  My guess is the student set up the problem vertically, multiplied 5 x 2, carried the one and added 1 + 1 + 1 to get a 3 in the tens place.  Just a guess though. She went on to tell us that 24% of the 6th grade students got this problem incorrect. Scary.  The problem 12.6 x 10 was posed and we went through the same steps of guessing the two incorrect responses. 39% of the interviewed 6th graders answered this incorrectly and the two most frequent incorrect responses where 120.6 and 12.6.  We watched a couple videos of the students’ incorrect reasonings.  The most interesting clip for this problem was a student who answered the question as “120 and 30 fifths.”  The student had multiplied 12 x 10 to arrive at the 120, but then wrote 6/10 as 3/5 and multiplied by 10 to arrived at 30/5.  Marilyn pointed out that while not conventional, it is the distributive property and what an excellent opportunity it would be to ask students if that answer is correct. Knowing the student errors that occur on these problems can help guide your classroom instruction.  It was interesting to me that the majority of the teachers in the room could name the most frequent incorrect responses and yet these mistakes are still occurring.  If we know they happen, what are we doing to stop them from happening?

With a few technical difficulties in the beginning, we were running about 5 minutes behind schedule. That didn’t leave much time for fractions, however Marilyn briefly discussed comparing fractions such as 3/8 and 9/16.  She stressed the importance of having students explain the “because” part of the answer.  She said because of the easy equivalence of 16ths with 3/8 and 9/16, she suggested then asking 3/8 or 5/6 to elicit different solution pathways.

Marilyn’s discussion and examples of the Math Reasoning Inventory demonstrated the importance of teachers listening to students and using those conversations to improve the connection-making and relationship-building in classroom instruction.

If you are interested in more math recaps, visit Dan’s recap site! Awesome stuff!

-Kristin, Math Minds

Embracing Disequilibrium

2 Replies

There seemed to be two common threads among the majority of sessions at NCSM this week: CCSS and Standards for Mathematical Practice. It was close to impossible to find a session without those terms somewhere in the description. Whether you love them or challenge them, the CCSS offered a wonderful opportunity for rich mathematical discussions & examination into best practice.

It was Ruth Parker who closed her session by saying, “Looking ahead, we need to embrace disequilibrium, liberate students and teachers to step outside of their comfort zone.” This statement was NOT what you saw in every session description, however for us, truly captured the essence and heart of the conference.

Embrace Disequilibrium.

Not a phrase you often hear in education, right?

To help us along in our post-session discussion, we immediately pulled up our dictionary app: Disequilibrium (n) – loss or lack of balance attributable to a situation in which some forces outweigh one another. Synonyms: changeability, fluctuation, fluidity, unpredictability, variability…

As teachers, we like balance. We live on fixed schedules. We arrive at school at a specific time, each subject has an allotted time, lunch for 1/2 hour and so on. So for us, this thought of imbalance opened up a plethora of questions. What does that mean for math education going forward? Does it mean the same thing for everyone? Can you observe it in a classroom? How does it impact professional development for our teachers?

Disequilibrium in the way we plan our units of study: Plan for “the math” in a unit instead of planning how to teach students to solve the math at the end of unit assessment.

Disequilibrium in the way students problem solve: Don’t rush to rescue students from their confusion. Let them struggle. Allow them the satisfaction of learning something new and knowing they can do it.

Disequilibrium in the way we assess our students: Assessment opportunities arise often, take advantage of them at all times, do not just reserve assessment for “quiz/test day.” Make it formative and meaningful in guiding instruction.

Disequilibrium in the way students talk in the classroom: No more raising hands and sharing answers one at a time. Students create arguments, listen to one another, critique each other’s reasoning, and work collaboratively.

Disequilibrium in the way we pose problems to students: Engage them in meaningful math tasks. Pose investigations with student-driven inquiries and entry points for all learners. Make connections, discover relationships, and make a habit of asking, “Is it always true?” or “Does this always work?” to challenge the learners.

Disequilibrium in the way we organize our PD: No more one size fits all when we train our teachers. Design PD like you would want to see teachers teaching students. Be engaging, do math, involve administrators, use technology (shout out to Twitter here), coach teachers, create teacher leaders, model and reflect on best practice.

Marilyn Burns, Kathy Richardson, Jo Boaler, and many others by whom we were beyond impressed, all sent the powerful message that EVERY student can learn. We, as educators, must meet students where they are, embrace mistakes as a learning opportunities, engage students in challenging tasks with multiple pathways to a solution, and encourage mathematical discourse in the classroom. To do this, we must be fluid in our instruction and let student thinking create imbalance.

Embrace Disequilibrium.

Be okay with discomfort, be okay with imbalance, thoughtfully shake things up, be changeable, your students will thank you!

Mathematically Yours,
Kristin and Nancy, Math Minds

Is the generalization ever too much?

Leave a reply

We love having students make generalizations in math class. Is this always true? Will it work for every number? If students can answer those questions, we feel we have created a successful learning experience for students, right?

Well, after attending a session today on supporting teacher learning in the CCSS, it led me to question if there is a time when the generalization hinders a learning experience? For example, we sat down to this problem: “Find all possible dimensions of a rectangle where the area equals the perimeter.” We worked through the problem individually and then together as a group. After coming up with 6×3 and 4×4 by guessing and checking, we started forming some ideas towards a generalization that would push students past guess and check. After some discussion, we concluded that the dimensions couldn’t be two odd numbers and there was a time when the area grew more rapidly than the perimeter so those larger dimensions would not work. After trying to set up an algebraic equation to formulate a generalization, we stopped to share as a group.

Long story short, we were told the generalization to find all possible dimensions with equal area and perimeter was that if a rectangle with sides a and b, a = 2b/(b-2). Now my question is this, does this generalization alienate a large group of students? I know as adults, we persevered and created viable arguments; however at a certain point we saw no entry point for many 6th grade students to answer this question. As adults, we were even at a loss after a certain point of working. Attentions started to stray and side conversations began. On the flip side, if i had left without the generalization, I would have left frustrated. But did that generalization help me make connections between length of sides and area and perimeter? I would argue not.

I feel that if we are going to have students make generalizations, there needs to be connections among entry points and when there is not a visible connection, I am at a loss.

Any general thoughts ;)?
– Kristin

NCTM 2013 – Choices, Choices, Choices…

Leave a reply

We are finally en route to Denver! So far we are loving the free baggage (just made the 50 lb limit whew), drinks, and snacks on Southwest; however after leaving the runway & pulling out our NCSM packet of sessions, we are completely overwhelmed and exhausted!

Before choosing our sessions, we brainstormed a bit about what we wanted to get out of the conference as a whole, what were we definitely looking for, as well as what we were not. Nancy was looking for sessions that sounded thought-provoking, interactive and align philosophically with her beliefs on how students learn. I went more with weeding out what I was NOT looking for in a session. I did not want sessions based in “policy” or “newest trends” in education, testing, or tiers of RTI. I wanted sessions, like Nancy, centered around improving student learning and strategies to move more teachers in the direction of best math practice.

It was obviously easy to choose the big sessions led by presenters whom we have used their resources in our own practice, educators we look to for inspiration, and persons who have contributed to us becoming the math educators we are today. Jo Boaler, Marilyn Burns and Kathy Richardson were three easy session picks!

Now the tough part begins….

Monday options:

9:30-10:30
“Exploring teachers’ practices of responding to students’ ideas” – Amanda Milewski
“Constructing arguments in the elementary classroom: struggling and excelling students in the classroom community”-Susan Jo Russell
“Helping teachers implement research-based instructional practices”-Karin Lange
“Thinking beyond the content: using mathematics as a vehicle to teach reasoning”-Marilyn Trow (leaning toward this one)

10:45-11:45
“Linking problem solving and the standards for mathematical practice”-Robyn Silbey
“How to differentiate your mathematics instruction, K-5”-Jayne Bamford-Lynch (leaning toward this one-Nancy)
“Reaching all learners by differentiating instruction in grades 3-5”-Janet Caldwell
“What is fluency and why is it important”-Skip Fennell (leaning toward this one-Kristin)

12:15-1:15
“Interviewing students to learn about algebraic reasoning Grades 3-5”-Virginia Bastable
“Differentiated coaching: providing each teacher with the support to reach each student”-Jane Kise
“Defining effective learning experiences for educators in a CCSS classroom”-Marji Freeman

1:30-2:30
“Increasing teacher quality with differentiated PD”-Jennifer Taylor-Cox

2:45-3:45
“Enhancing mathematics education using the iPad”- Amanda Lambertus

4:00-5:00
“Noticing and wondering as a vehicle to understanding the problem”-Annie Fetter

As you can see we still have some narrowing down to do in our am sessions so any feedback is much appreciated! Do you know any of the presenters? Any topic jump out at you? Why?

Check back soon for our upcoming sessions and session recaps!!

Mathematically Yours,
Nancy & Kristin, Math Minds

Well, it is about time….

Leave a reply

We are so excited to finally be getting our blog up and running!  Since joining Twitter this year and reading so many interesting posts, we are ready to dive into the blogging world!

We have decided that in order to make it dramatic, we will begin with an actual launch (of a plane that is) & write our first post on our way to Denver for NCSM!

We will keep you posted on our session choices, comment on sessions we attend and report back on any other great math conversations we encounter on our journey!

If there is anything particular you would love to hear from the conference, let us know in the comments!