Just like the launch of a lesson shapes how students access the mathematics, the structures we use during group work support what they do once they’re in it. In these moments, who talks, who listens, and whose ideas move the work forward can either widen or narrow the thinking that happens. Group time can be a place where rich, collaborative work happens, but it involves much more from the teacher than giving the directions ‘work with your group,’ ‘turn and talk,’ or ‘think pair share.’ While a curriculum can provide teachers with helpful suggestions, the uniqueness of each group of students places the responsibility heavily on the teacher, which makes sense. Only the teacher knows their students and the dynamics within each small group. Small shifts in how we organize students, position their ideas, and support their discussions can dramatically impact both the mathematical practices that students engage in as they work and the mathematical thinking that students bring to the whole group discussion afterward.
After exploring ways to launch a lesson, the next opportunity for quick, high-leverage adaptations comes when students begin working together. From the moment we ask students to collaborate to the moment when we circulate and listen, the structures we choose can either uncover students’ thinking or unintentionally limit it. Thoughtful approaches to group work can support collaboration, build mathematical habits of mind, and strengthen the sense of community we hope to see in our classrooms. In this post, we’ll look at quick, in-the-moment ways to support group work so every student has an opportunity to contribute and every idea has a chance to surface.
Alternate Ways to Work in Groups
Instructional Challenges: When students jump into group work without clear structures for talking and listening, it becomes easy for one person’s ideas to dominate while others disengage. Without intentional support, some students simply “go along” with the loudest or quickest thinker, and opportunities for deeper reasoning are lost. Additionally, when students stay in the same assigned seats, groups can become static. While this consistency can help early in the year as a community is forming, it can also limit the range of perspectives and mathematical ideas students encounter over time.
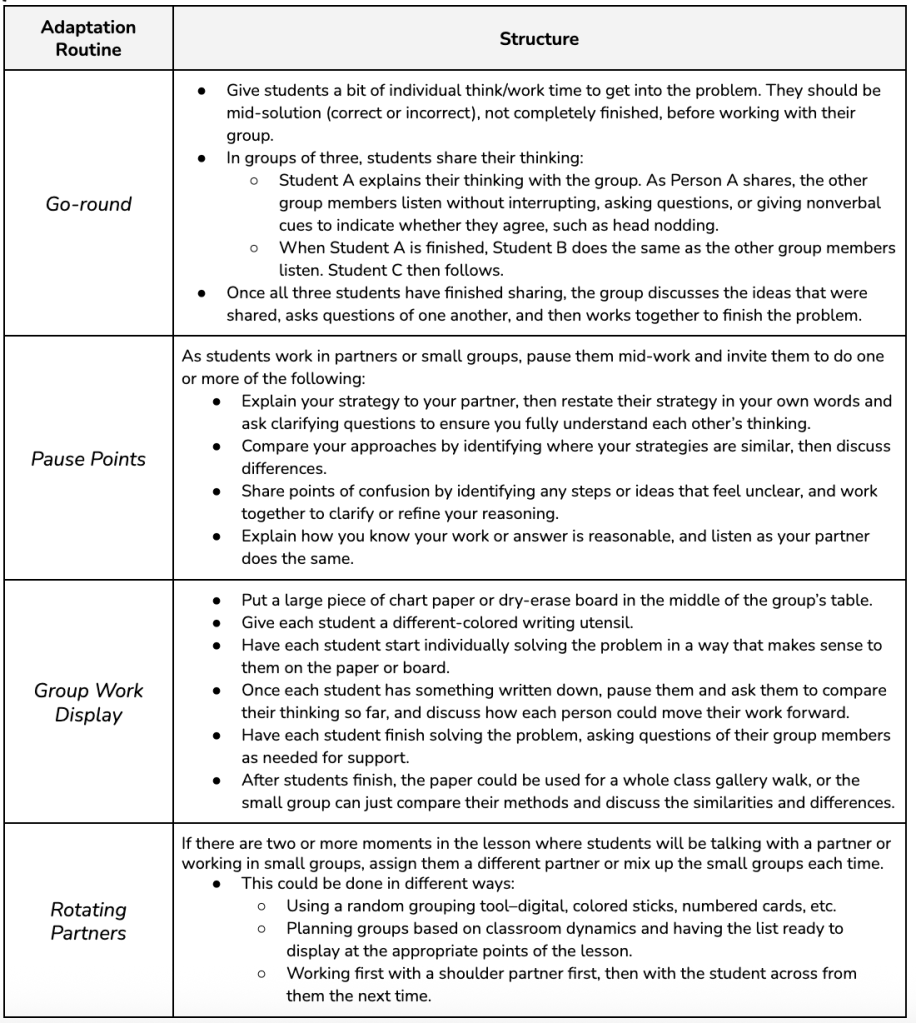
Each of these routines require students to articulate their ideas and listen to the ideas of others. One routine I love to support these practices is Talking Points. It didn’t really fit with the others in the table, but I wanted to mention it here as I close out the post. This routine includes giving each group a carefully crafted statement (for example, a prompt about multiplication or division), and asking students to respond by agreeing, disagreeing, or saying they’re unsure while explaining why. Because everyone at the table gets a chance to voice their ideas, and then they collectively wrestle with different perspectives, students often reconsider or deepen their understanding about the topic at hand. Finally, when the groups come back together for a whole-class reflection, all students benefit from a wide array of reasoning. I have a collection of blogs about Talking Points in the K-5 math classes here if you are interested in trying them out!
Try it!
In your next PLC or planning session, review the activities in an upcoming lesson. As you read through each problem, discuss:
- What questions should I ask students to discuss in small groups that will move their thinking toward the mathematical goal of the day?
- What structures can I use to ensure all students have the opportunity to share their ideas and have their ideas heard by others in the class?
- Which of the four group work structures will you use to support students as they learn together?*
*If you’re planning with your grade-level team, each person can try a different structure and then compare the affordances of each. I’d love to see what you try! Share your ideas in the comments or on IG (@kgraymath)!
Next up will be routines for supporting student learning as they engage in problem contexts, in particularly word problem sense-making strategies.