Category Archives: Uncategorized

2nd Grade Counting,Unitizing, & Combining

The other day, I began writing up my lesson plan for a second grade class I was teaching today. I drafted the lesson, got feedback, revised and ended with this plan, around the 5 Practices, going into the classroom today.

I started the lesson, as I planned, with the students on the carpet like they typically are for a Number Talk. I wrote the sentence “There are 12 people in the park.” on the board and asked them to give me a thumbs up if they could give me a math question I could ask and solve from that statement. A couple students shared after a bit of wait time and I was getting a lot of even/odd talk or questions that involved adding more information to my original sentence. I asked them to turn and talk and one little girl next to me said they could find the number of legs. When I called the group back together I asked her to share her conversation with her partner and after that, hands shot up like crazy. It ended with a board that looked like this…

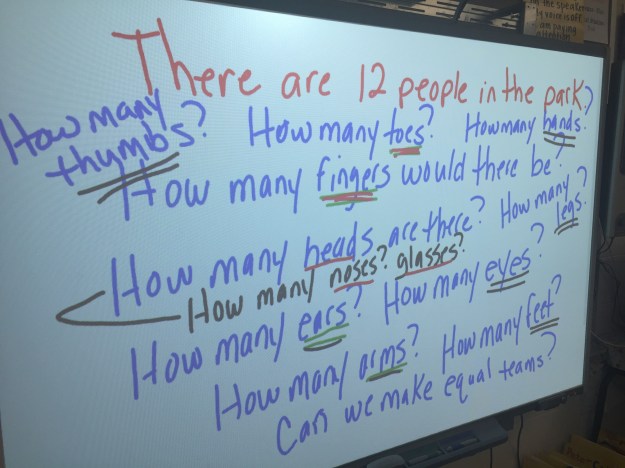
I asked them if we could think about any of these in the same way? I tried to underline the “same thoughts” in the same color, but they started making connections that is got a bit mixed. A lot of there conversation turned to numbers and so I started a new slide and asked what numbers they thought of when they read those problems and why. I recorded what they were thinking…

I really liked this opening talk (15ish minutes) and really didn’t want to let them go when it was time for their recess break in the middle of math class. So, they lined up and left for 30 minutes.

When they got back, we recapped the numbers and then I gave two groups question #1 and the other two groups question #2. They had individual time to get started and then they worked as a group to share their thinking. Knowing that I was going to be trading seats at groups for them to share their problem with another table, I was walking around looking for varying strategies so I didn’t trade seats and have a whole table who solved it all the same way.

They did a beautiful job working in their original group. I saw students who had different answers for the same problem talking out their strategies and arriving at a common answer. I saw students practicing how they were going to explain it to the new table they visited. I saw students who were stuck working through the problem with their tablemates. I can tell there is such a safe culture established by Lauren, the homeroom teacher. They trade seats, shared their problem and then I had to readjust my plans.

At this point, I wanted the tables talking about what was the same and/or different about the two problems but I was running out of time. In order to pick up with that conversation tomorrow, I decided to have them come to the carpet and I chose two papers (of the same problem) that had the same answer but different strategies. I asked the students privately if they would want to share and they were both excited so I put them both under the document camera and had them explain their work. I thought they was similar enough for students to easily see they both drew the figures out but as I walked around I heard the 1st student counting each one by ones and the 2nd student counting by twos after he wrote the equation. I had them explain their work and asked the class to think about what was the same and what was different and we discussed it. Here are the two I chose:

FullSizeRender 10.jpg FullSizeRender 12.jpg

They pointed out all of the similar things such as feet, people, two’s (but were counted differently), and the same answer. The difference was the equation which was an important thing to come up. I saw quite a few students with the correct answer but incorrect equation. A lot arrived at 22 by counting by wrote 7+2 as their equation so that was an important thing that a student pointed out.

I only had 5 minutes left, so I decided to collect their papers and pick up with the sequencing and connections tomorrow. Which I kind of love because it gives me time to be more thoughtful about how they should share them and also time to talk to their teacher about what I saw today.

So, from my previous plan, I am picking up here:

Practice 4: Sequencing

In the share, after each group has presented to the other groups, we will come to the carpet for a share. The sharing will be sequenced in the way I discussed in the Selecting part, asking students during each student work sample how it is similar and different than the ones we previously shared.

Practice 5: Connecting

The connecting I see happening through my questioning as we share strategies. I am still working on writing this part out and looking for the connections that can be made, aside from the picture to number representation connections.

The connections I would love to see students making throughout the work and sharing, is how we can combine equal groups. For example I would like the student who is drawing ones and counting them all to move to seeing those ones grouped as a 2 or a 5 depending on the context. I would love the student who is seeing the five 1’s as one group of 5 to now see that if they have 2 of them it will make a 10 and if we have 4 of them we would have 20 and really start looking at different ways to combine those groups.

The problem I am seeing in this plan is the differences in the two problems. As I sit here with the papers all over the table, I am struggling to make a sequence involving both problems. So, do I sequence a set for each problem and give each 1/2 of the class time to talk about the similarities and differences? or just choose one problem and go with that?

For problem 1, I like this sequence in moving from counting by 1’s to grouping them and then to the finding half of 34.

FullSizeRender 16 FullSizeRender 15 FullSizeRender 14 FullSizeRender 13

For question 2, I see this sequence from pictures to grouping them by people and dogs, the third shows the 8 composed but broken apart on the number line and the paper before it, and the last one starting at 14.

FullSizeRender 17 FullSizeRender 18 FullSizeRender 19 FullSizeRender 20

I collected their papers and asked them, in their journals, think about how many people and dogs there could be in the park if I just told them there were 28 legs. I thought that after their share tomorrow of this problem it would lead them into a nice problem from which some great patterns could arise. Here were a few I grabbed before I left:

FullSizeRender 9.jpg

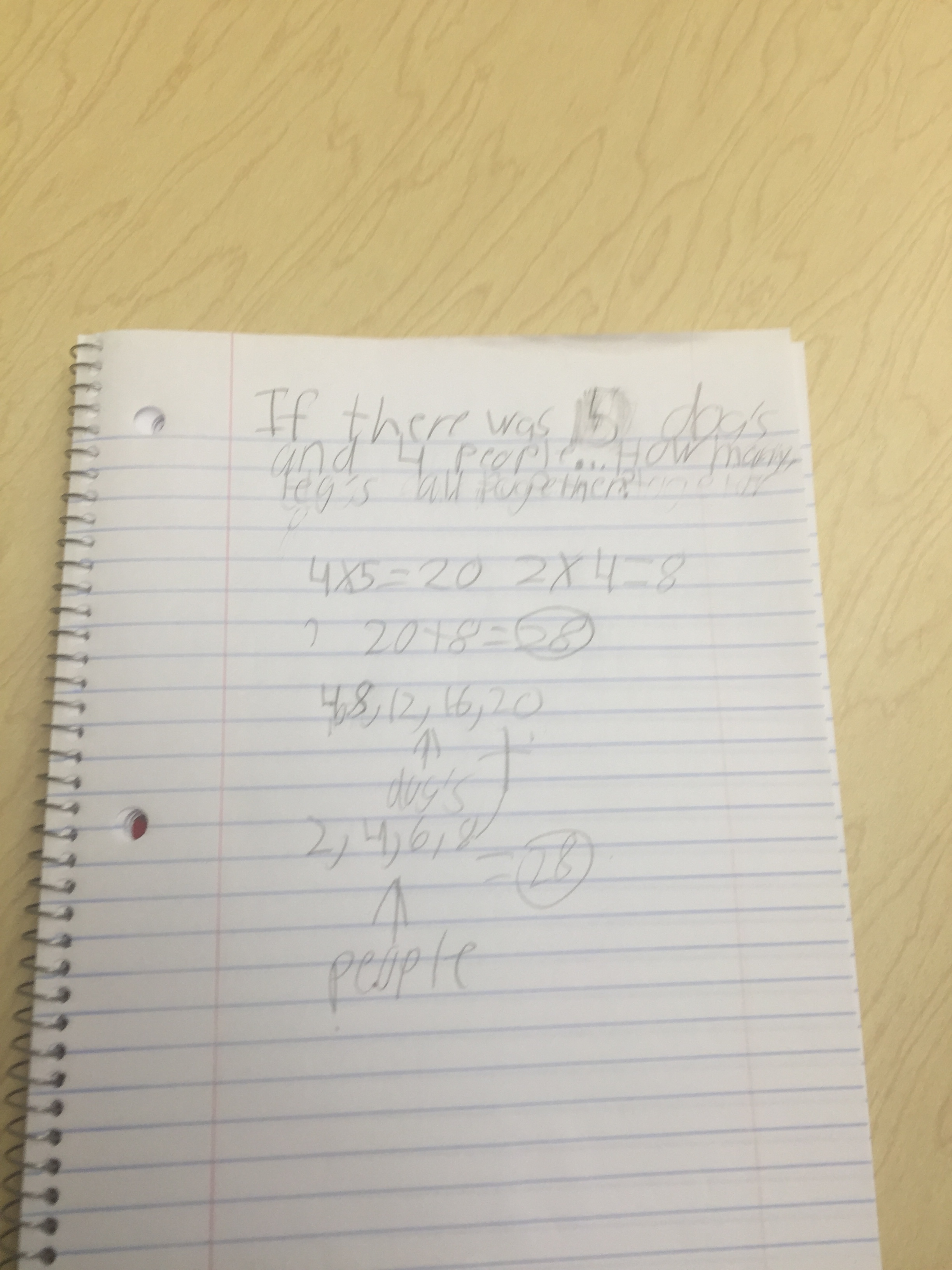
and this last one was getting at some really great stuff as she got stuck at 9 people and couldn’t figure out the number of dogs. I asked her to write what she was telling me!

FullSizeRender 8.jpg

Looking back, I would have probably chosen just one problem to work with to make it more manageable in sequencing and making connections during the share. Having two problems was nice as far as having them explain it to others, so I like that, but I am wondering if we did #1 through this process and then split for questions for #2 and #3.

I look forward to hearing how it goes tomorrow!

~kristin

Even or Odd…So Much To Think About!

5 Replies

At the end of the day, Lauren, a 2nd grade teacher and I started chatting about her upcoming lesson on even and odd numbers. I have done a lot of thinking about even and odds in 5th grade when we entered decimals, however I can honestly say I have not thought about it much more than a number being able to be broken into two equal parts or it can’t because there is 1 left over.

Enter this student activity page from Investigations…

Now, I know Investigations is so purposeful with how they structure their pages so I was immediately curious about the set up of this page and wondering why thinking about even and odd in these two ways was so significant. My mind went right to the foundation for the commutative property. For example, with 10, will each have a partner? yes, 5 pairs or 5 groups of 2 or 5 x 2. Can we make two equal teams? yes, 5 on each team or 2 groups of 5 or 2 x 5. I would like to extend this sheet to include a space for the expressions: 2+2+2+2+2 = 10 = 5+5.

Then of course I tweeted it and got this great stuff from Tracy:

So much great stuff to think about and I absolutely cannot wait to see how these students deal with conjectures and generalizations! I would love any more thoughts on this work because I am sure there is more great stuff in here!

-Kristin

//platform.twitter.com/widgets.js

Lunchtime Cafeteria Chat

8 Replies

It is amazing to me what a well oiled machine our cafeteria is each day! Amidst the near 800 students walking in and out, the volume of students all talking over one another, the perfectly timed staggered schedules, the forgotten utensils, and spilled food and drinks, the students still get in and out of there within 30 minutes each and every day without fail. The wonderful people working those lunches are absolutely amazing!

As I walk around the cafeteria, or even stand outside in the hallway, I hear all of the different types of conversations…some are about their lunches, or about their classes that morning, or possibly even about their classmates. However, at a glance around the cafeteria, there are other students who are not talking at all and some tables are even eating in silence. While I appreciate students who may want to eat in silence, I wonder if there are others who need a topic in which to engage in conversation?

When my colleague Erin suggested putting up some type of slide presentation on the projector screen on the stage during lunch, I thought it was a genius idea! She said it could be like the previews in a movie theater that everyone watches before the feature presentation. Like most ideas with me, we jumped right in. We came up with prompts for students to use as a piece of their conversations and spark interesting conversations around the cafeteria. We put 15 ideas together in a looping ppt, with a 30 second transition between slides.

Here are our first week’s slides:

It was so fun to walk around and see students pointing at the screen and offering what they thought the answer would be and explaining why! What a way of creating a student culture that demonstrates how differently and creatively we can all think about the same thing.

Like any idea, there are always ways to improve and this idea is no different! We have brainstormed ways to include pics of the students, our Peacemaker awards (shout outs for students and/or teachers who are caught doing great things -PBS), pics/fun facts about the teachers, and ways for all of the students to contribute ideas/prompts for the presentation. My colleague Melissa came up with the adorable name of “Chat-n-Chew” which is so much better than “lunch presentation” and offered to have a group of her students design future presentations and of course, they are the “Chat-n-Chew Crew.” 🙂 Each homeroom teacher will have suggestion forms for their students to send to Melissa’s 4/5 class to use in their presentation creation.

One day, I will get Erin on here to blog (I hope she is reading this) because she has so many wonderful ideas to share! 🙂

-Kristin

1st Grade Ten Frame Number Talk

1 Reply

I had the exciting chance to do a Number Talk with a 1st grade class last week! Looking back to where these students ended the year, I was fairly comfortable starting with ten frames and entering into talking about teen numbers within this context.

I started with the same ten frame I did in 2nd grade, that I talked about here. Looking back, I wished I had started with a full row of 5 just to talk more about how they saw it or just knew it in relation to the 10. Next time:)

I then wanted to see how they thought and talked about a full ten frame and teen numbers. Did they count on from 10, just know 10 + 5, and/or talk about teen numbers as 10 and some more? So I posed these ten frames:

The students had some wonderful explanations of how they saw the dots and established how they just knew the ten if it was full. Some added on by ones to 15, some knew 10 and 5 was 15, some counted by 5’s to 15 and then one student some creative grouping vertically by 6,6,and 3. So I then pushed them a bit on how they recorded the equations and I was excited to quickly get 10+5= 15 and 5+5+5=15.

My brain right now is algebraic reasoning all they way so I could not pass up the opportunity to do this:

10 + 5 = 5 + 5 +5

I asked them if they thought their teacher would mark that right or wrong and why? I had them turn and talk to a partner and after a quick raise of hands, I could see the class was split on whether it was right or wrong. I asked those who said it was wrong why and got what I was expecting…

“After the equal sign can only be one number, no plusses. If you changed those lines (equal sign) to a plus, then maybe it would be right.” In reading Thinking Mathematically and Connecting Arithmetic to Algebra, I am finding this is a huge misconception that students build from K.

I asked the students who thought it was right to explain why and I got two uniquely different ways of thinking algebraically about this equation.

“They are the same because 10+5 is 15 and 5+5+5 is 15 so they are the same.” This student is looking for balance, this side equals that side so it is equal. I could assume that given 12 + 6 = _ + 5 + 6, this student would think they need 7 more in the blank to balance both sides.

The second student said this:

“The 10 is a 5 and a 5, so it is the same as the other side.” This seemed quite different to me. It felt like a symmetrical way of looking at equations. He decomposed the numbers to prove they were equal by the way it looked. I could assume that given 12 + 6 = __ + 5 + 6, this student may decompose the 12 to 5+7 to find 7 is the number that goes in the blank to make it look equal. A bit different and something I really hadn’t thought about until now.

Thanks to Michael Pershan to making me think (obsess) over the ways in which students think about these in such different ways 🙂

These were the last two in my talk that I did not get to because these 1st graders had so much to say about the first two and I had so much to learn!

Looking forward to working so much more with these kiddos!

-Kristin

Making Schools A Safe Place for Teachers Too.

2 Replies

I so appreciate the fact that our district this year is focusing on really trying to make our PLC and PD time productive and meaningful for all of our teachers. We are finally having K-12 conversations around instruction and coherence of content, it is an exciting change! As we talked yesterday, I continue to realize how difficult it is to put systems in place that support teacher learning that, in turn, impact student learning experiences in the classroom.

All morning we discussed things such as:

where we (as teachers, schools and districts) are in terms of understanding the standards
how teachers are using standards in planning
how we are currently assessing those standards
student awareness of the standards
how we are reflecting on our teaching

…etc. All very important things.

We then talked about how we improve upon where we are and necessary structures to make improvements happen. In that discussion, I heard these types of things…

Teacher ownership because they see the need for change
Small changes
Have a plan
Accountability
District dedication of time to the effort (PD days)
Less mandates
Admin role

…etc. Again, all very important conversations to have.

Then we watched this clip:

The question, “What’s Your Leaf?” was posed. What do we see as the biggest obstacle in our way of growth/change? I can list a number of things that I would anticipate are justified obstacles for many teachers, however I keep coming back to one thing….Fear. I see fear as the leaf. Fear of being vulnerable, fear of opening up classrooms, fear of exposing what we don’t know, fear of repercussions of mistakes…etc.

So, how do we truly make change and improve teaching and learning?

Make our schools a safe place for teachers as we try to make them for students.

I would love to see schools be more like the blogs I read and conversations happening on Twitter. I want teachers to feel they have a voice and have important things to say. I want the conversations among teachers during the day to be about content, teaching, student work. I want them to challenge each other’s thinking and not be ok to always agree to disagree.

Someone recently asked me how I became so openly reflective about my own teaching and the answer is simple…I realized a had a voice, people were interested in what I was saying and I finally became ok with not knowing. It is hard to be vulnerable in teaching because it is such a personal thing for us, our job is not just a job, it is us.

My goal this year in working with teachers is first and foremost creating a safe place where math conversations around teaching and learning are the norm. Where we can be comfortable saying “I don’t know” and it is ok and there are no negative repercussions.

-Kristin

PLC Brainstorming

8 Replies

As I move back into the math specialist position at my school this upcoming year, I have really been thinking a lot about the way in which our district PLCs are structured and, as a whole, how we treat each subject area as separate professional development entities. As an elementary classroom teacher, we either participate in a math PLC or a language arts PLC twice every week during our planning time. While it feels like it would work content-wise for the teachers who are K-3 and teach everything, it becomes a bit trickier when teachers are departmentalized in 4th and 5th grade. Not that there isn’t a need for everyone to be involved with both content areas due to everyone teaching RTI groups, however it still feels like there is a disconnect and sadly can lead to the “waste of my time” mantra because it doesn’t feel applicable to what they are doing in their core classroom work.

So, the question I am working through, is how can we do this better?

The more I engage in math conversations around the book Connecting Arithmetic to Algebra, the more I begin to see the structure of future PLCs evolve. (To catch up on those convos, @Simon_Gregg did a nice recap here: http://followinglearning.blogspot.fr/2015/06/mathematical-reasoning.html) It may seem odd to pull other content area ideas from here because the book is about amazing math reasoning and thinking, but I really see huge potential in this idea of “Making Claims” across all content areas. Thinking about this, I dug into the ELA CCSS, found these standards and started thinking about how this process sounded similar to our book discussions:

Upon further reading I came upon this ELA unit on Making Evidence Based claims: https://www.engageny.org/resource/making-evidence-based-claims-units-ccss-ela-literacy-grades-6-12

Then I moved into the Next Generation Science Standards and in a quick search I found this…

I just see so many potential connections here to have everyone engaged and leaving feeling like the PLCs were worth the time invested.

There is much more learning to be done on my part in the content areas, but I am seeing a way to structure our PLCs so they are not so much “by subject area” each time, but more “by ideas and reasoning process.” Questions I am thinking about….

– Could we center PLCs around ideas such as “Making Claims?” Talk about what students do during this process, how we foster the environment and share with each other content-focused work to look for similarities/differences?

– Could we center PLCs around various purposes for writing, or my favorite “Journals”? Discuss how and why we use them and share student work to discuss?

– Could I use the PLC time for this “Idea work” and have content knowledge come out more during coaching and hopefully some type of Math Lab as Elham has talked about?

As usual, not many answers and many more questions! Would love thoughts around this so I can work on making it useful and applicable for everyone next year!

-Kristin

Patterns and Perseverance

Growth Patterns In Both Math AND My Understandings!

Choral Counting – Decimals

10 Replies

The first day back to school after NCSM/NCTM is definitely an exciting one! I was excited to see my students, hear and see them doing math again, and incorporate the amazing things I learned at the conference with them. It is always great when I can go to a session, regardless of the grade level focus, and be curious how my students would engage in the activity. For example, I went to an amazing session on counting by Kassia (kassiaowedekind), Elham (@ekazemi) and Allison (@allisonhintz124). While the session focused on whole numbers, I began thinking about how I could take this same practice of Choral Counting and use it in my classroom. I have to admit, while my first thought was what my students would think about during this activity, I also had my own curiosities in the teacher organization of the work. Does writing them horizontally vs vertically bring out different noticings or patterns? or How does how many I put in each row or column affect their thinking about it?

Luckily, we are currently working on multiplication of decimals and I thought this would fit in just perfectly. I did some brainstorming and decided for my first class we were going to choral count by 0.3, record horizontally and vertically and have 1/2 of the class focus on the horizontal while the other 1/2 focused on the vertical. I was curious to see if they saw different patterns emerge. I started at 1.5 because I wanted a number that would hit a whole a couple times in our round but not make the “10” of them makes a whole number so obvious.

I did find that many of the same patterns emerged, however it definitely looked more intuitive for the students to look for patterns in the direction they had recorded.

Here are a few students who used the vertical recording…

You can see this student first noticed the 1.5 going up and down each column. She then noticed a diagonal pattern and could place the 9 where it would go had we continued.

This student started with thinking about them as whole number by multiplying them by 10. I love the last noticing because it makes such a beautiful connection to his first statement. When I asked him to clarify his thinking he did stipulate that you had to start at 3 for that to be true.

There is a beautiful statement in here that says she knew 0.3 is 10% of 3 because between each whole number there are ten 0.3’s. Lovely.

Here are some examples of horizontal, again, many of the same patterns…

This one was not so much focused on the patterns of numbers increasing or decreasing, but instead found that if you switched the whole number and tenths, the number would also be hit by a multiple of 0.3. Interesting to figure out why that works and when that doesn’t work. They left REALLY excited to keep working on this one. How much do I love the “I thought of this!” next to it!

I asked one student, who seemed content with his noticings before they shared as a table if he could think of any equations that matched the number patterns he saw while he waited.

I asked him where he saw the last one in the numbers and had him record it in Educreations: https://www.educreations.com/lesson/view/multiplication-decimals/31049585/

When the second class came in, I decided to switch up the number in each row to five (thanks Elham for that suggestion) to see if differences came out. Here was our board:

i definitely like the 5 in each row better than the 6, a lot more patterns emerged, quickly. It pretty much screamed patterns! We shared them all and I asked each table to pick one they wanted to explore deeper and figure out why it was happening.

This student said, “If you pick any number, go up and then over two the tenths digit will be one more than the starting number. It also works if you go down and then over two.” He explored that one here:

It was a wonderful first day back! My students and I really enjoyed the choral count (although they all spelled it coral:)! It was a very safe feeling knowing they were all saying it together, a bit different than the counting around the class.