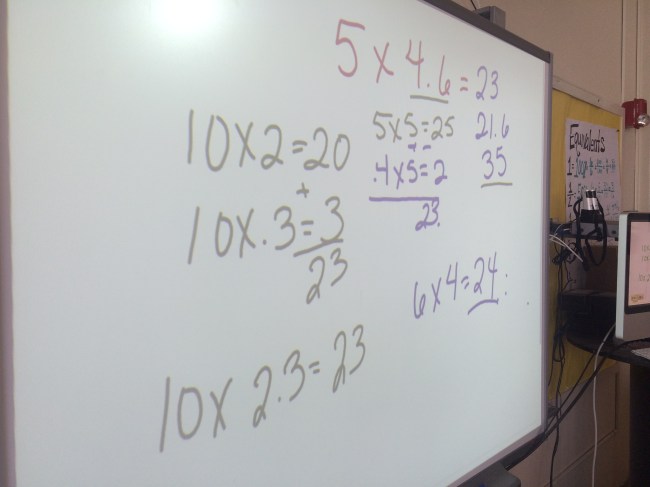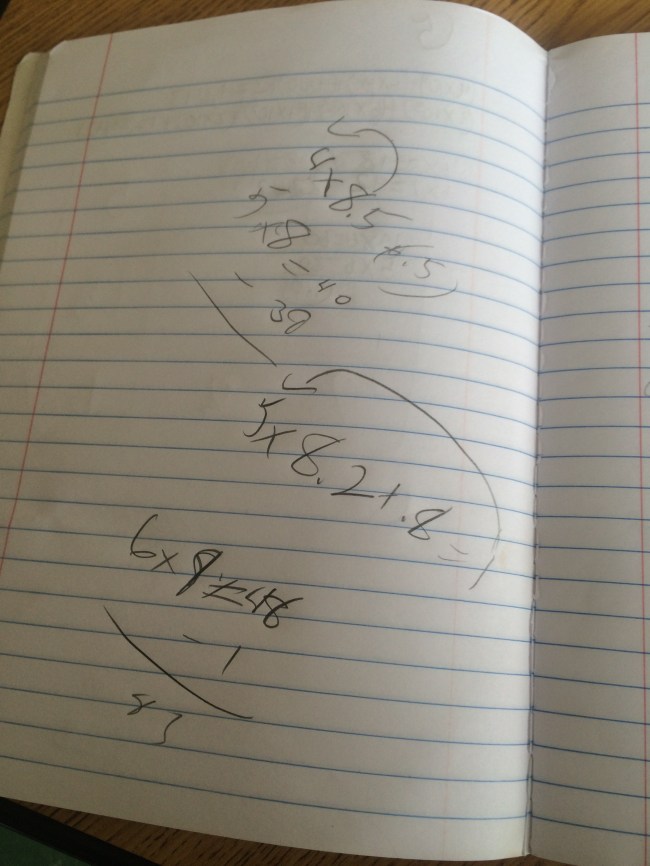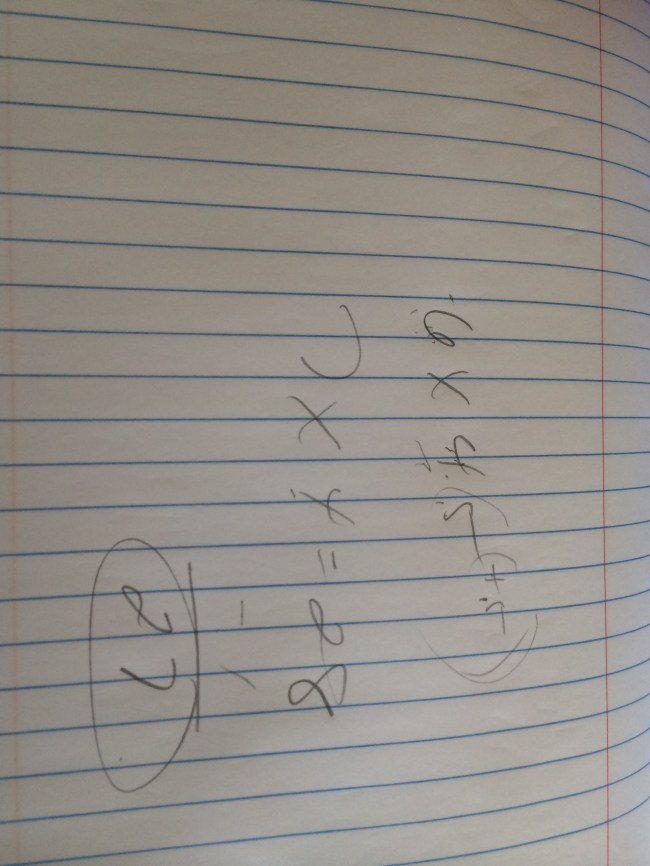During the majority of the professional development planning I have been doing this summer, I feel like one of the common threads is Number Talks. After each conversation, more and more questions start spinning in my head….questions about how often to implement, questions about teacher recording, and most importantly, questions about their purpose.
I wasn’t inspired to write them all down until I read @gfletchy’s post: http://gfletchy.com/2014/07/22/on-you-marks-get-set-number-talks/. BTW *If you do not follow his blog, you most definitely should, great stuff*
Questions/Thoughts about Number Talks:
1 – Through the math conversations, it fosters a safe, collaborative culture in my classroom.
2- Their conversations embody the Mathematical Practices in my eyes. Their use of structure of the number system, creating viable arguments, critiquing the reasoning of others and repeated reasoning is always music to my ears.
3 – I struggle with purpose…is the purpose a particular strategy? That is how Parrish’s book frames it. There is a string, centered around a certain strategy. Not that other strategies do not emerge, but the numbers are such that they lend themselves to a particular path. So, my conclusion is this – When doing a number talk string, I am not pushing a certain strategy, but instead, encouraging the students to truly think about the numbers before simply “computing.” I do want students to think that if they are multiplying 39 x 45, to think about 40 and taking a group away rather than breaking both numbers to get 4 partial products. In thinking about the numbers more deeply, they call on their conceptual understandings to develop fluency.
4 – Is the purpose to generate connections between strategies? I do think there is a benefit to putting up one problem and recording all of the strategies to make connections between them. I use that as a formative assessment as to what my students know and also to identify misunderstandings/misconceptions that emerge.
5 – Fawn’s blog has sparked an interest to branch into more visual patterns to switch it up a bit. What that would look like in my 5th grade class, is something I need to work through but I think the algebraic reasoning behind them would be intriguing.
6 – I Completely agree with Graham, they must be a daily routine, they build computational fluency (based in conceptual understanding) and must not just happen on Fridays! Also, it is important for students to use their Number Talk reasonings in other math work.
7 – Teacher recording is something I am still trying to improve upon daily. Recording their thinking is harder than one would think! Also, I find WHAT I write can change the direction of the talk itself.
I am a huge proponent of Number Talks and would love to see our elementary work with them to start to move into the middle/high school classrooms!
-Kristin