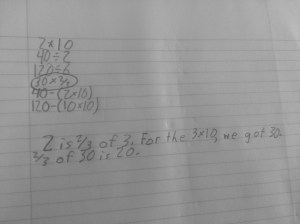The math ego in me wants to preface this post by saying, I understand how to find patterns, I understand how to graph lines, I understand slope and y-intercept and could graph any line based on that information….etc; however, more and more I find the need to truly reexamine the way in which I “understand” concepts in math. This unit is one of those times. Math ego aside, I have left class so confused over the past couple of days, calling my math phone-a-friends for tutoring! I blogged about the beginning of the unit here and since then my head has been spinning.
We opened the unit reading growth stories of children that gave the child’s age at age 2 and how they grew. The students created data to match the story and graphed it on this graph (which at the time I didn’t think too much about the way the x and y-axis were set up)
 We had great conversations about how they determined their data, the steepness of lines based on the change, and what steady growth looks like. So far I was completely in my comfort zone and felt prepared for what was coming….then I decided to try out some number talks with patterns and I still cannot decide if was a mistake or the best thing that could have happened in this unit!
We had great conversations about how they determined their data, the steepness of lines based on the change, and what steady growth looks like. So far I was completely in my comfort zone and felt prepared for what was coming….then I decided to try out some number talks with patterns and I still cannot decide if was a mistake or the best thing that could have happened in this unit!
To avoid recapping everything I have typed in my previous blogs, I am going to skip the actual number talks strings but instead focus on the things that have come up form the students that have pushed my understandings over the edge during them….
In a string of numbers with a constant change, students were getting amazing at finding the 10th term and then generalizing to find any term. At this point, all of the patterns had started with either the number we were counting by or a multiple of that number. When starting from a multiple of the number we were counting by, the students had great arguments and come to the conclusion that you didn’t need to add the number you started on, but instead the last multiple before the 1st term in the pattern. For example, counting by 9’s starting at 27, 36, 45, 54… the tenth term we would say is 9 x 10 + 18 while some students insisted it was 9 x 10 + 27 because that is where we started. This part poses a problem later on….
After asking the students what was important when thinking about patterns, I was feeling great with responses like this (at the bottom of the page).
 Then we jumped back into their student activity book into contexts of animal growing and finding the growth patterns of each. The first animal at birth is 1 cm and grows five centimeters each year. They filled out the table and found the pattern: 5n+1.
Then we jumped back into their student activity book into contexts of animal growing and finding the growth patterns of each. The first animal at birth is 1 cm and grows five centimeters each year. They filled out the table and found the pattern: 5n+1.
Anyone see the problem that is coming yet?
One student (who was adamant during the number talk earlier) starts questioning why we add the 1 on here but in the number talk we went back to find the last multiple and then added that on. If this one is true why didn’t we add the 27 in the earlier problem when counting by 9’s? Just then I realized there is something else that is very important when looking for patterns that I completely missed, the term number. After class, I started asking myself…why does that completely change how we solve for a term number and can you make any number a particular term? How does that effect the line and pattern? Then when we graph it where do I start the x-axis? Like the graph earlier in this post, does the term 1 meet at the y-axis? These were the first of many of my questions.
Going into class today, I completely expected this idea to arise, and it did. We counted by 5’s starting at 2:
2, 7, 12, 17, 22…
I ask: Tenth term?
They respond: 47 and 52
They talk it out, count it out and come up with the two possible equations of 5×10-3 or 5×10+2. There are lots of looks of confusion because they know when they count it ends at 47 but they remember the work in the book from yesterday. I have them go back to the growth pattern from yesterday. I sent them back to their table to talk about how it could be both and I was happy to see them start to think about the what we were naming the terms. We revisited the context in the book and I wrote that first growth pattern out on the board as 1, 6, 11, 16, 21… and asked what the 10th term is. In their table they had the 10th year as 51, so some were confused to see it pop us as 46 when they counted it out to double check….I loved this one….
We revisited the context in the book and I wrote that first growth pattern out on the board as 1, 6, 11, 16, 21… and asked what the 10th term is. In their table they had the 10th year as 51, so some were confused to see it pop us as 46 when they counted it out to double check….I loved this one….
 But many were starting to see that the 10th year was really the 11th term because of the “0th term” as they called it.
But many were starting to see that the 10th year was really the 11th term because of the “0th term” as they called it. 
 So I seemed to have this concept under control….until we moved to graphing….I had them predict if they would be the same line or different lines? Majority went with the same line, one was just one jump ahead of the other. Even in graphing them, there was some confusion that I struggled to answer because of our work in the book earlier…does the origin have to be the 0 term on the y-axis or could they start with the 1st term on the y-axis? When we graphed the earlier graphing stories they started with year 2 on the y-axis, but there was growth before that, so why didn’t it start out on 2 on the x-axis. I completely could be missing something, but because it felt right in the moment I went with 0 at the origin. We graphed them and found them parallel, but I left the class uncomfortable with how the graphs were presented and how number patterns, like our number talk, transfer to graphs.
So I seemed to have this concept under control….until we moved to graphing….I had them predict if they would be the same line or different lines? Majority went with the same line, one was just one jump ahead of the other. Even in graphing them, there was some confusion that I struggled to answer because of our work in the book earlier…does the origin have to be the 0 term on the y-axis or could they start with the 1st term on the y-axis? When we graphed the earlier graphing stories they started with year 2 on the y-axis, but there was growth before that, so why didn’t it start out on 2 on the x-axis. I completely could be missing something, but because it felt right in the moment I went with 0 at the origin. We graphed them and found them parallel, but I left the class uncomfortable with how the graphs were presented and how number patterns, like our number talk, transfer to graphs.

They still had many questions (as did I) about how we number the terms. How could we decide if it is term 0 or term 1? We had a brief chat about how the context could dictate that. One group said they think it is like this….”If you walk into a casino with $1 and then every machine you go to, you hit for 5 dollars, then $1 would be the zero term because you had it when you got there.” They continued, “Then if you went it and won $1 on your first machine and then $5 every machine after that, $1 would be your 1st term.” We had to wrap it up for the day but I look forward to thinking about this a bit more with them.
I asked them to write what they thought was important now in looking at patterns after our work today..

 In conclusion, I have SO much to re-learn about thinking about patterns and graphing. I am still muddled in thinking around so many ideas that I am having trouble organizing them into a nice list at this point. This is somewhere the unit definitely does not go, but these students constantly push my thinking and I loving these final 8 days of it:(
In conclusion, I have SO much to re-learn about thinking about patterns and graphing. I am still muddled in thinking around so many ideas that I am having trouble organizing them into a nice list at this point. This is somewhere the unit definitely does not go, but these students constantly push my thinking and I loving these final 8 days of it:(
On a side note, I had students do a quick fill in the blank from Justin’s Twitter post a month or so ago…Math is _______. I got some amazing ones, but this was one I snapped a pic of on my way out today because I loved it and it fit my mood….
 -Kristin
-Kristin