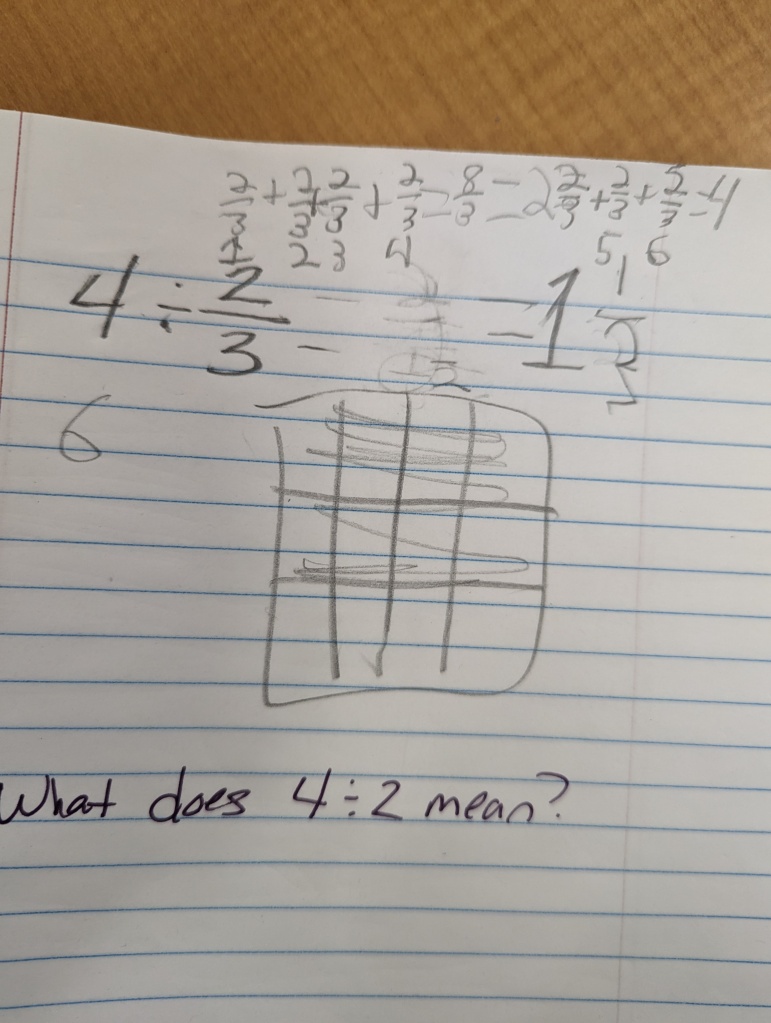It is posts like Lisa’s most recent one that make me long for more collaboration K-12. I have to admit, when I saw her Twitter post with the words pre-calculus and simplifying complex fractions, my inclination was to skim right by because I would not understand the post anyway. Literally, my only recollection of simplifying complex fractions like the one at the beginning of her post is through a set of procedures I was explicitly taught step by step. However, when I looked at the accompanying image that showed fraction division, I was curious how my understandings of fraction division connected to her pre-calculus work.

I loved reading Lisa’s process of making the math accessible for her students because I am sure many would have felt like I did if shown the CPM opener from the very beginning. It is that same process of thinking about what students know and how we can build on it that made me get out my journal and start sketching out connections I was making as I read. In no time, my journal was full of problems, diagrams, concepts, questions and every tab on my computer referenced the progressions, standards, references linked in Lisa’s post, and a blank email to Kate and Ashli to jot down my questions for them about the math. Talk about a wonderful rabbit hole to be going down.

The more I read and reread this post, the more I think it could lead to many more posts connecting how students are introduced to ideas in elementary school, the impact it has on later work, and the questions I have as I go. My questions revolve around not only the math, but also how these mathematical ideas build, how our representations impact student understandings, and how there are times when a problems lends itself to one way of thinking versus another.

During my first read, two things I wondered were:

1. How does the way the fractions are written impact the way I think about them?
2. What happens when I have two ways of thinking about fractions and two ways of thinking about division?

How does the recording of the fractions impact the way I think about them?

As the post progressed from an image of a complex fraction to one of fraction division, I felt like Lisa must have felt, wondering what students may know about the complex fraction and why they may struggle. My initial thought was they may not understand that a complex fraction is even division. This may not be the case for most, however based on what I remember from high school, I saw complex fractions as one thing I did operations on. As an elementary school teacher, it seems similar to the difference between seeing a fraction as a number (introduced in 3rd grade) versus seeing fraction as division (introduced in 5th grade).  As I looked at CPM’s complex fraction and how it was written, I only thought about it as multiplying the numerator by the reciprocal of the denominator because of how I was taught. However, when I looked at the fraction division problem written horizontally, I found myself attending more to each fraction as a number, using what I know about division to find the quotient. Less intimidating to me solely because of the way it was written on the paper.  I wonder if this compares a bit to how we record computation problems horizontally versus stacked during number talks to encourage thinking about a problem versus always relying on the algorithm?

I know the fraction division problem means the same thing written either way, but how they are written impacts my thinking a lot. From an elementary perspective where we spend so much time attending to developing understanding of fraction as a number, I am not inclined to really think about what it means to divide the two terms when written as a complex fraction. To that end, I wonder if the opening problem written one way versus another evokes a different meaning for some students?

Knowing that there are things to be learned in between the problems listed below, but in terms of seeing the complex fraction as division where I think about the individual pieces as things in their own right, is one possibly a small transition to the other for me or students like me?

Lisa – I would love to hear more about the transition prompt between the fraction division problems the students were solving and the CPM problem. I think that is a really important piece of what you did so beautifully in this lesson.

What happens when we have two ways of thinking about fractions and two ways of thinking about division?

I think about fractions in the two ways I mentioned above: as a number and as division.

I think about division in two ways: how many groups? and how many in each group?

First, fractions: In 3rd grade, students learn a fraction is a number in which the numerator indicates the number of pieces and the denominator (as the denominator of a unit fraction) represents the size of the piece. For example, we say 3/4 is 3 pieces the size of 1/4. This understanding and associated language are so beautiful when students use it to compare fractions and create equivalent fractions. In my 5th grade class, my students were comfortable using complex fractions such as1/2 / 3 when talking about 1/6 because they were thinking ½ a piece the size of ⅓ is ⅙. No division, just reasoning about the pieces and their size. When comparing 4/9 to 5/7, students would use the reasoning that four and a half ninths and three and a half sevenths are equivalent to a half so 5/7 is more than a half and 4/9 is less than a half. I saw a glimpse into how that thinking was not helpful when they asked what happened when there is a fraction in the denominator. This is where understanding fraction as division would have been more helpful. 

In 5th grade students also learn about fractions as division. In terms of sharing situations, they learn that 5 things shared by 3 people results in each person getting 5/3 of the things or 5 divided by 3. In these situations, thinking about 5 pieces the size of 1/3 is not particularly helpful in solving, but division is. However, when it comes back to interpreting the solution, 5 pieces the size of 1/3 is needed.

Questions I am thinking about at this point:

• How does the complex fraction in the post relate to either or both of these ways to think about fractions?
• How does the way we represent fraction division relate to one or both of these ways to think about fractions?

Now, division: In 3rd grade, students learn division in two contexts: how many in groups and how many in each group.  In 5th grade, students use those understandings to divide whole numbers by unit fractions and unit fractions by whole numbers. Those two meanings of division carry into middle school to divide fractions by fractions and conceptually understand the reason we multiply by the reciprocal.

After reading Kristin and Bill’s series of posts on fraction division, I am now constantly thinking about how the context (interpretation) for division impacts the way students represent and solve a problem. I know changing the way I think about the division context changes how I represent the problem as well as how I operate with the reciprocal.

Questions I am thinking about at this point:

• Does one context of division connect more closely with the CPM complex fraction problem?
• Does the visual fraction model of the the division problem impact the way students approach the complex fraction problem?
• • Is an array representing both fractions being divided helpful in this complex fraction?
  • Is one bar model representing both fractions on one helpful in this complex fraction?
  • Is one way of representing it more helpful than the other?

Obviously, I have a lot to read about how a problem such as the one Lisa posed progresses after middle school but after seeing the division of fraction problem,  I am even more intrigued to see how these ideas progress from the time they are introduced. I am so curious when certain ways of thinking are more helpful than others and how we can construct learning experiences that help all students have access to the mathematics in a lesson in the way Lisa did.