Often when I do a Number Talk, I have a journal prompt in mind that I may want the students to write about after the talk. I use these prompts more when I am doing a Number String around a specific idea or strategy, however today I had a different purpose in mind.
Today I was in a 4th grade class in which I was just posing one problem as a formative assessment to see the strategies students were most comfortable or confident using.
The problem was 14 x 25.
I purposefully chose 25 because I thought it was friendly number for them to do partial products as well as play around with some doubling and halving, if it arose. When collecting answers, I was excited to get a variety: 370,220, 350 and 300. The first student that shared did, what I would consider, the typical mistake when students first begin multiplying 2-digit by 2-digit. She multiplied 10 x 20 and 4 x 5 and added them together to get 220. Half of the class agreed with her, half did not. Next was a partial products in which the student asked me to write the 14 on top of the 25 so I anticipated the standard algorithm but he continued to say 4 x 25=100 and 10×25=250 and added them to get 350.
One student did double the 25 to 50 and halved the 14 to 7 and then skip counted by 50’s to arrive at 350, instead of the 300 she got the first time. I asked them what they thought that looked like in context and talked about baskets of apples. I would say some were getting it, others still confused, but that is ok for now. We moved on..
Here was the rest of the conversation:


I felt there were a lot more wonderings out there than there was a need for them to write to a specific prompt, so I asked them to journal about things they were wondering about or wanted to try out some more.
I popped in and grabbed a few journals before the end of the day. Most were not finished their thoughts, but they have more time set aside on Wednesday to revisit them since they had to move into other things once I left.
What interesting beginnings to some conjecturing!



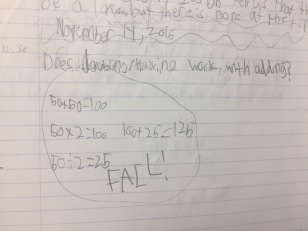

The last conjecture of tripling and dividing by 3 works, too. The pattern holds because while what they are doing seems like magic, it is simply shifting. The real learning comes as they explore the pattern that makes it work! As a co-teacher of mine said recently… math is the only subject where everything we do can be undone!
LikeLike
Absolutely! I have found that students first stab at providing evidence for a claim is the “See, it works here and here and here” kind of method, which I think is extremely valuable way of approaching it. I thought I would let them play around with that for a bit and then ask for a representation (since they did mention the area model in the number talk) that would prove why those numbers are behaving in the way they are. I am revisiting them on Monday to discuss what they have found so far and will try to nudge them into other evidence for the conjecture!
LikeLiked by 1 person
I hope you will share what you find!
LikeLike
Pingback: #LessonClose | Becoming the Math Teacher You Wish You'd Had
Pingback: Representations and Manipulatives and Tools and Things | Becoming the Math Teacher You Wish You'd Had